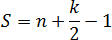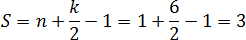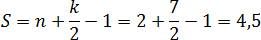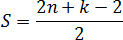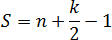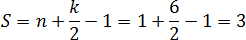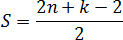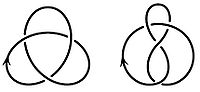Что значит узлы сетки
Метод узлов в задаче B5
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
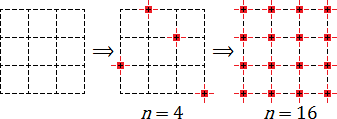
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
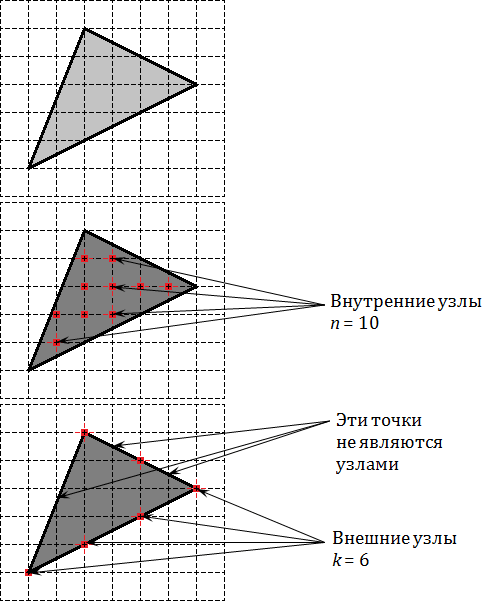
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
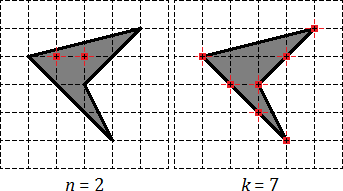
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
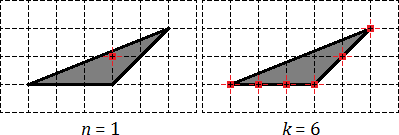
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Метод узлов
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
Задача:
Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача 2:
Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
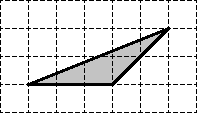
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача 3:
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
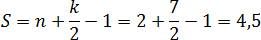
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»:
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Сегодня мы научились считать площади фигур в задаче B5 методом узлов. Повторим, что для начала введят два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5
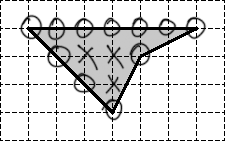
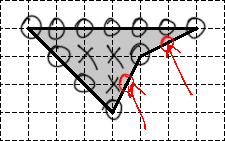
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Крестиками обозначены внутренние узлы. Очевидно, их количество Кружками обозначены граничные узлы. Их общее количество равно
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Теорема. Пусть дана фигура с внутренними узлами и граничными узлами. Тогда площадь этой фигуры считается по формуле:
S = n + 0,5 k − 1
Вот так все просто! Главное — запомните, это число внутренних узлов, число граничных узлов.
В нашем случае мы уже подсчитали, что Подставляем полученные числа в формулу и получаем:
Мы получили ответ: площадь четырехугольника
Ответ: 7,5
Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.
Узел (математика)
Содержание
Понятие математического узла
Узлы — предметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен, физик-теоретик, работающий в Принстоне.
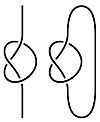
Чем отличается математический узел от узлов, которые завязывают на галстуках или на шнурках ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой — в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутая несамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, то есть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.
Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником, узел на рис. справа — восьмёркой. (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направление обхода кривой, это направление изображается стрелкой.)
Группа узлов
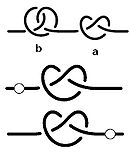
Если считать узлы кривыми, концы которых уходят в бесконечность, то умножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, на которой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а, b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая) является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла, завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a, затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения.
В этой системе есть единичный элемент, но нет обратных.
Компьютер развязывает узлы
Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к (более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер.
Имеет место
Лемма Рейдемейстера. Если узел можно развязать (превратить в окружность) в пространстве, то его плоскую диаграмму можно распутать на плоскости с помощью операций Рейдемейстера.
Что значит узлы сетки
В широком понимании слово «сети» означает различные по конструкции и назначению орудия лова рыбы. Их можно разделить на две большие группы:
Рассмотрим обычные, самые распространенные жаберные рыболовные сети для любительской рыбной ловли, которая проводится по лицензиям. Такие сети тоже делятся на несколько категорий:
• ставные сети (одностенки, двухстенки и трехстенки, рамные сети) – это легкие сети, которые применяются на слабом течении, на озерах, прудах и водохранилищах;
• сплавные сети с разным количеством стенок – более тяжелые сети, которые используются на течении, благодаря специальному поплавку-кресту (гагара) сети дрейфуют по течению вместе с лодкой.
Любой увлекающийся рыбной ловлей человек может оформить разрешение на лов рыбы сетями. Купить рыболовные сети проще всего в нашем интернет-магазине. Для изучения этой, кажущейся простой рыбалки, есть смысл купить самые простые, бюджетные сети в готовом, или как говорят «в посаженном» виде. Но гораздо интереснее, посадить сети самому.
Сейчас никто не вяжет сетное полотно своими руками, как это было полвека назад. Тогда существовали практически полностью самодельные авторские сети, которые передавались от отца к сыну, за ними ухаживали, их постоянно ремонтировали долгими зимами. Сейчас рынок заполнили антиподы старинных сетей – так называемые «китайки», доступные по цене низкокачественные сети из тонкой слабой лески, предназначенные не для рыбаков, а для браконьеров. Такие сети рвутся от вынимаемой рыбы, стоят они недорого их часто забывают извлечь из воды такие «рыболовы». Гибнет масса рыбы. Дискредитируется само понятие сетной рыбалки.
Как сделать посадку рыболовных сетей своими руками
Посадка рыболовных сетей своими руками — долгий процесс по сравнению с машинным способом. Но такая снасть более уловистая и мягкая в работе.
Как делается посадка рыболовной сети
Посадка — это крепление сетевого полотна к шнуру, которое можно сделать вручную, челноком или машинным способом.
Для того чтобы сделать из полотна орудие для лова, сетное полотно надо посадить на верхнюю и нижнюю подборку. Для верхней подборки применяется плавающий шнур, этим облегчается постановка сетей и их распутывание.
Длина верхнего и нижнего шнура
Нижний грузовой шнур на 20−30% длиннее, чем верхний. Эта разница длин делает сетевое полотно провисающим. Но для верши такое провисание нежелательно, т.к. рыба будет запутываться.
Если верхний плавающий шнур будет длиннее, чем нижний, тогда верхняя часть будет уловистей.
Такая посадка может применяться для лова сигов на дне или у поверхности речки; как правильно сделать посадку, можно определить, зная вес и плавучесть шнуров.
Из-за различных расстояний между узлами сети отличаются и длины верхнего и нижнего шнуров. Чем больше промежутки между узлами, тем длиннее посадка. Орудие для лова с разными ячейками имеет различный посадочный коэффициент (ПК).
Используемые узлы
На прочность узлов влияет метод их завязывания и используемые материалы. Узлы для посадки рыболовных сетей выполняются несколькими способами:
Леска затягивается в ту сторону, в которую она закручивается сама.
Способы посадки
Есть несколько способов посадки:
Существует несколько способов посадки сети — с помощью финского метода или прямоугольного. При финской длину верхней подборы уменьшают, а нижней увеличивают. При прямоугольной длина шнуров верхней и нижней подборы одинакова.
С использованием челнока
Челнок применяется для ручного плетения сетеполотна и для посадки его на подборы. Челнок пропускается через крайние ячейки, которые привязываются к подборному шнуру. Снова пропускается и фиксируется. Повторять надо до тех пор, пока все ячейки не закрепятся.
Не нужно для ускорения работы делать большие промежутки между узлами, т.к. это нарушит положение полотна в воде.
С использованием специальных машин
Производить орудия для лова можно с помощью машинной вязки. Весь процесс плетения выполняется в автоматическом режиме. На одном станке для вязания могут выпускаться изделия с различным размером ячеек. Размер ячейки зависит от установленных параметров и настраивается вручную. Станок может вязать любым типом ниток.
Посадка сети своими руками
Чтобы сделать орудие лова своими руками, нужны такие инструменты:
Плетение выполняется так:
Чтобы в будущем правильно поставить сеть, при посадке используют грузила и поплавки.
Для чего нужна веха
Веха — специальная линейка, с обеих сторон которой делаются зарубки. Потом отмечают значения интервалов между узлами, прикладывая веху к сетевому шнуру.
Требования к посадке в зависимости от предназначения сети
Орудия лова рыбы бывают такими:
До того как ставить сеть на реке, надо определить место концентрации рыб. Однозначных рекомендаций, как поставить рыболовную сеть, нет, но нужно учитывать, в каких реках рекомендуется использовать те или иные снасти.
Как сделать посадку рыболовных сетей своими руками Ссылка на основную публикацию
Устройство сети. Верхняя и нижняя подбора
Любая самая простая одностенная сеть состоит из нескольких элементов:
Сеть из нескольких стенок отличается от простой сети наличием дополнительного сетеполотна (одного или двух) с очень большой ячеей, в среднем, 150-200 мм. Такие полотна называются «ряж» и служат для образования мешков, из усаженного основного полотна с мелкой ячеей, которые сами образуются при попадании крупной рыбы.
Рамные сети – это обычные одностенные сети, которые дополнительно усаживаются по высоте на 20%. Это достигается с помощью вертикальных прожилин из более толстой нити или лески. Кроме того, рамные сети могут иметь и горизонтальные прожилины, которые тоже немного усаживают полотно. В результате, в сети образуется очень уловистая система прямоугольников-карманов, которые выполняют роль мешков в многостенной сети.
Выбор грузового и плавающего шнура зависит от материала и размера ячеи сетеполотна. Для поимки некоторые видов верховых рыб используются плавающие сети. Поэтому вес грузил или грузового шнура совместно с весом сетеполотна и самих шнуров должен быть меньше водоизмещения поплавков или плавающего шнура. Для большинства тонущих сетей ситуация обратная. Вес оснащенной сети должен быть больше грузоподъемности плавающего шнура или поплавков. Сеть должна тонуть медленно, поэтому разница в весе не должна быть более 20%.
Подбор поплавков и грузил для рыбалки в различных условиях также соответствует принципам, которые изложены для подбора грузовых и плавающих шнуров.
Сплавные сети широко используются на больших реках. Они имеют более прочные подборы, более тяжелые грузила и грузоподъемные поплавки. В низовьях сибирских рек основная ловля всех видов сиговых рыб осуществляется тонущими сплавными сетями. Прочность их такова, что при донном зацепе, сеть удерживает большую моторную лодку на сильном течении. Естественно, что верхняя подбора, которая идет к лодке, должна быть пропущена через носовой кнехт.
Способы посадки рыболовной сети
| Наботов Рустам (автор) |
Популярный способ посадки рыболовной сети
Простейший способ посадки рыболовной сети – насаживание на сетную подбору крайнего ряда ячей. Чтобы в процессе лова сохранить посадочный коэффициент, нужно вдоль подборы примерно через 0,5 м прикреплять к ней одну из ячей.
Данный способ посадки очень распространен в нашей стране и за рубежом. Но этот способ имеет недостаток: во время установки и выборки сетей рыбаку приходится захватывать руками и саму подбору, и часть сетеполотна, которая к ней прилегает. Из-за этого подбора быстро изнашивается.
Такой способ посадки лучше использовать только в недоступных ветру и волнению водоемах во время ловли с небольших лодок, при небольшом объеме улова. Когда сетевое полотно сильно натягивается, его тонкие нити врезаются в пальцы рук.
Эта посадка хороша при условии большого размера ячеи сетного полотна.
Вышеописанный способ посадки рыболовных сетей нравится рыбакам Архангельской области. Сети эти длиной 25 м, материалом для подборы служит капроновая веревка диаметром 3 мм.
Нить посадочную, нити для подвязывания грузил и поплавков и боковые прожилины изготавливают из нити 93,5 текс х 3.
Из пенопласта ПВХ делают 21 поплавок совокупной массой 0,14 кг, а из проволоки – грузила в количестве 21 штуки совокупной массой 1 кг. Размеры ячей составляют 34-45 мм.
Обычные одностенные рыболовные сети, как правило, сажают на огниво, его длина составляет 15-20 см. Нужную длину огнива и количество надеваемых на него ячей устанавливают, исходя из размера ячеи.
По возможности нужно не допускать использование длинных огнив с большим числом ячей между прилегающими посадочными узлами, иначе материал рыболовной сети быстро износится из-за неравномерного натяжения нити сетеполотна. В идеале на огниво должно приходиться всего 2 ячеи.
Тогда все нити сетеполотна натянутся равномерно. Также делают ставные рыболовные сети, предназначенные для ловли нерпы в Белом море. У этих сетей шаг ячеи 150 и 180 мм. Длина сети в посадке составляет 25 м при посадочном коэффициенте 0,5.
Капроновый сеточник в диаметре равен 6 мм, его применяют для подборы сети, а из нити 93,5 текс х 18 делают боковые прожилины. Для подвязки и посадки грузил применяют такую же нить; надевать поплавки следует именно на подбору.
Поплавков нужно 28 штук с шагом ячеи 150 мм, а грузил – 24 штуки с шагом ячеи 180 мм. Масса каждого поплавка – 25 г, каждого грузила – 100г.
В случае неравномерного распределения основных нагрузок между подборами, разумно брать для нижней и верхней подборы разную длину огнив. Например, на огниво верхней подборы нанизывать по 4 ячеи, на огниво нижней подборы – по 2. Кроме того, для подбор могут быть использованы разные способы посадки.
Посадка на бегу
Наиболее простой и выполнимой посадкой является посадка на бегу. Но есть случаи, когда ее применение нецелесообразно.
Так, например, ячея мелкоячеистого полотна, расположенная между двумя прилегающими огнивами, сильно деформируется и натянется, тогда в этом месте нить может быстро порваться. Поэтому для посадки мелкоячеистой сети существует 2 способа.
Первый – между огнив остается одна ячея свободная, а у рыболовных сетей для лова салаки и килек пропускаются 2 ячеи.
Посадка на бегу широко распространена и для посадки рыболовных сетей, и для всех других видов орудий лова. Связано это с легкостью ее осуществления, удобством работы с сетью, а также с тем, что в процессе лова при интенсивном волнении сетеполотно почти не наматывается на верхнюю подбору.
Посадка на огниво не используется по отношению к морским рыболовным сетям, так как при сильном волнении крайний ряд ячей стремительно перетирается о посадочную нить.
При посадке на огниво всегда нужно помнить, что при натянутой подборе вся вертикальная нагрузка достается ячеям, у которых нити расположены под посадочным узлом.
Поэтому, когда на сеть направлены большие вертикальные нагрузки, посадку на бегу лучше исключить.
Материал для посадки
Для посадочной нити нужно брать только высококачественный материал. Прочность нити должна в 2 раза превышать прочность нити крупноячеистой рыболовной сети, не имеющей опушки, либо быть прочнее в 2 раза крайней нити опушки обычной рыболовной сети. Посадочная нить должна быть не тоньше 450 текс.
При разумном подходе посадочная нить крепится к подборе посадочным или выбленочным узлом. Подборы и посадочная нить должны быть изготовлены из растительных материалов.
А вот капроновые нити и веревки из-за своей гладкости и эластичности будут вести себя хуже: даже самый тугой узел в процессе использования развязывается, при этом некоторые огнива удлиняются, а некоторые укорачиваются, следовательно, правильность посадки нарушается.
Самый распространенный тип узла – посадочный. Чтобы он не скользил по подборе, нужно удлинить конец иглицы и выпилить в нем углубление. Конец иглицы просовывается между прядями подборы, на него надевается ходовой конец нити посадочной, протаскивается сквозь веревку, и в образовавшуюся петлю продевается иглица, и затягивается петля.