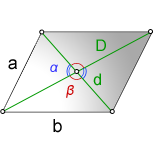
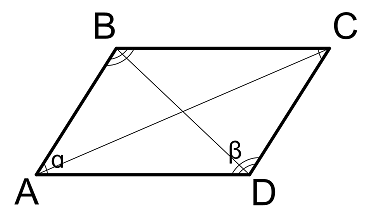
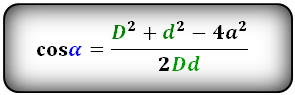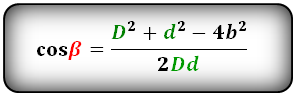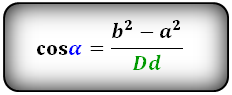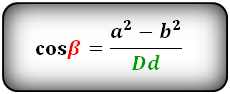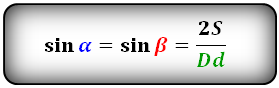Что значит угол между диагоналями параллелограмма
Найти угол между диагоналями параллелограмма
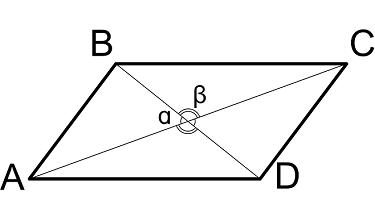
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β
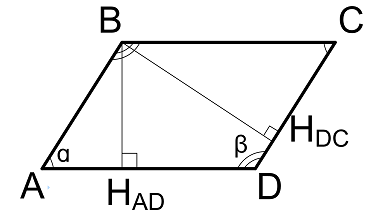
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и диагонали:
Формулы соотношения острого и тупого углов между диагоналями:
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы параллелограмма
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
Признаки и свойства параллелограмма
Формулы стороны параллелограмма
Длины сторон через диагонали и угол между ними
Длина стороны через диагонали и известную сторону
Длины сторон через высоты и угол между сторонами
Формулы диагоналей параллелограмма
Длина диагонали через стороны и углы между ними
Длина диагонали через стороны и известную диагональ
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями
Формулы углов параллелограмма
Косинус острого угла
Косинус тупого угла
Синус острого и тупого угла через площадь и стороны параллелограмма
Формулы углов между диагоналями параллелограмма
Косинус острого угла через стороны и диагонали
Косинус тупого угла через стороны и диагонали
Синус острого и тупого угла через площадь и диагонали
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Какой угол между диагоналями параллелограмма?
Тем не менее, под каким углом пересекаются диагонали ромба?
В любом ромбе диагонали (линии, соединяющие противоположные углы) делят друг друга пополам под прямым углом (90 °). То есть каждая диагональ разрезает другую на две равные части, и угол их пересечения равен всегда 90 градусов.
затем, как построить параллелограмм с двумя диагоналями и углами?
Ответ: Ниже приводится конструкция параллелограмма.
тогда какова мера каждого угла в параллелограмме?
Найдите угол в параллелограмме: пример вопроса №1
Пояснение: У параллелограммов сумма углов 360 градусов, но также имеют совпадающие пары углов на концах диагоналей.
Встречаются ли диагонали прямоугольника под прямым углом?
Как видно на фотографиях слева, диагонали прямоугольника не пересекаются под прямым углом (они не перпендикулярны). (Если прямоугольник не является квадратом.) И углы, образованные пересечением, не всегда имеют одинаковую меру (размер). Противоположные центральные углы имеют одинаковый размер (они совпадают).
У ромба 4 прямых угла?
Какая связь между диагоналями ромба?
Являются ли диагонали ромба биссектрисой?
Диагонали как биссектрисы угла
Как построить параллелограмм с двумя диагоналями?
Равны ли диагонали параллелограмма?
Диагонали параллелограмм равны. Противоположные стороны и противоположные углы параллелограмма равны. И эти противоположные стороны и углы составляют два конгруэнтных треугольника, причем две диагонали являются сторонами этих двух конгруэнтных треугольников. Значит, диагонали параллелограмма равны.
Что нам нужно, чтобы построить параллелограмм?
O Длина его параллельных сторон. Измерение внутренних углов. Две смежные стороны и один угол.
Как найти диагонали параллелограмма?
Рассекают ли диагонали параллелограмма пополам?
Теорема: диагонали параллелограмм каждый пополам Другие. … Верно и обратное: если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом. Стр. 3. Теорема: Противоположные углы параллелограмма конгруэнтны друг другу.
Диагонали параллелограмма?
Равны ли диагонали параллелограмма? Диагонали a параллелограмм равны. Противоположные стороны и противоположные углы параллелограмма равны. И эти противоположные стороны и углы составляют два конгруэнтных треугольника, причем две диагонали являются сторонами этих двух конгруэнтных треугольников.
Две диагонали прямоугольника равны Почему?
Да, диагонали прямоугольника равны. Это потому, что две диагонали гипотенуза двух прямоугольных треугольников, образованных диагоналями. Поскольку высота и основание двух треугольников равны, по теореме Пифагора гипотенузы треугольников также равны.
У прямоугольника четыре прямых угла?
Делают ли диагонали прямоугольника пополам под углом 90 градусов?
Каждый из внутренних углов прямоугольника составляет 90 °, в результате чего сумма внутренних углов равна 360 °. Диагонали прямоугольника делят друг друга пополам..
У ромба все углы 90?
У всех параллелограммов 4 прямых угла?
В параллелограмме если один из углов является прямым, все четыре угла должны быть прямыми углами. Если четырехгранная фигура имеет один прямой угол и хотя бы один угол другой меры, это не параллелограмм; это трапеция.
Есть ли у параллелограмма два угла по 90 градусов?
Решение: Параллелограмм можно определить как четырехугольник, две стороны s которого параллельны друг другу, а все четыре угла в вершинах не равны 90 градусам или прямым углам, тогда четырехугольник называется параллелограммом.
Какая связь между диагоналями?
Другими словами, точка пересечения диагоналей (пересечения), делит каждую диагональ на две равные части. Каждая диагональ делит прямоугольник на два равных прямоугольных треугольника.. Поскольку треугольники совпадают, они имеют одинаковую площадь, и каждый треугольник имеет половину площади прямоугольника.
Каковы 4 свойства ромба?
Как узнать, пересекаются ли диагонали пополам?
Формируют ли диагонали ромба прямые углы?
Пересечение диагоналей ромб в форме 90 градусов (прямых) углов. Это означает, что они перпендикулярны. Диагонали ромба пересекают друг друга. Это означает, что они разрезают друг друга пополам.
Делают ли диагонали прямоугольника пополам под углом 90 градусов?
Диагонали прямоугольник делят пополам. … Это означает, что прямоугольник является параллелограммом, поэтому: его противоположные стороны равны и параллельны. Его диагонали пересекают друг друга. Диагонали ромба В любом ромбе диагонали (линии, соединяющие противоположные углы) делят друг друга пополам под прямым углом (90 °).
Параллелограмм. Формулы, признаки и свойства параллелограмма
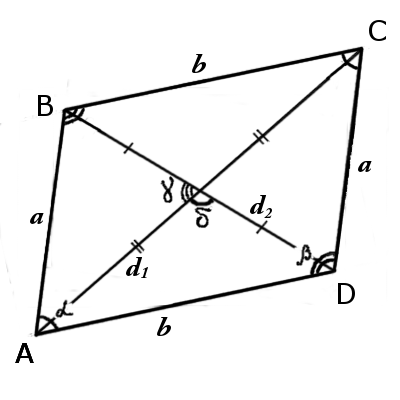 | 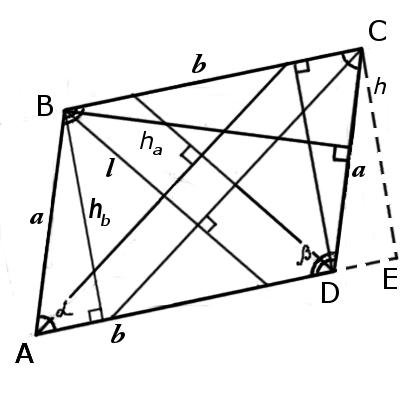 |
| Рис.1 | Рис.2 |
Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.