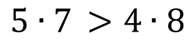Что значит сравни выражения

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений

Перечень вопросов, рассматриваемых в теме:

— Что такое числовые выражения?

— Как правильно читать и записывать числовые выражения?

— Как выполнять порядок действий, если есть скобки?

— Как сравнить два выражения?

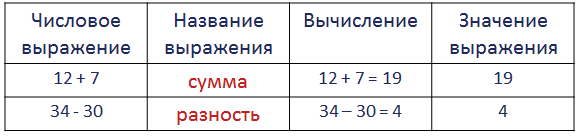
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.

Значение выражения – это результат выполненных действий.

Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.

Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.

Основная и дополнительная литература по теме:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40

2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27

3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16

Теоретический материал для самостоятельного изучения

Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.

Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.

Кто из них вычислил верно? Решил верно, Миша.

Запишем пример, который решали дети правильно:

Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.

Посмотрим на запись.

Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».

Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.

Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.

К числу 10 прибавить разность чисел 8 и 3.

Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.

Давайте сравним значения двух выражений:

Сначала найдем значение каждого из выражений и их сравним.

Источник

Сравнение значений выражений

Урок 3. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Сравнение значений выражений»

· разобрать, каким образом сравнивают выражения;

· показать что такое двойное неравенство;

· ввести понятия «строгое неравенство», «нестрогое неравенство».

Прежде, чем приступить к рассмотрению новой темы, вспомним, что:

Например, выражение 10(2 + 1,5) является числовым.

Выполнив действия этого числового выражения, соблюдая правильный порядок действий, получим число 35, которое называют значением данного числового выражения.

А теперь, чтобы разобраться, каким образом сравнивают значения выражений, решим следующую задачу.

Результат сравнения можно записать в виде следующего неравенства:

Таким образом, для любых двух числовых выражений можно установить, равны их значения или не равны. Если они не равны, то можем определить, какое из них больше и какое меньше.

Мы разобрались, как сравнить два числовых выражения. А как же быть с выражениями, содержащими переменные.

Давайте сравним значения выражений:

Видим, что для разных значений переменных результат сравнения выражений с переменными может оказаться различным.

Иногда перед нами может встать задача установить, между какими числами заключено значение выражения.

Источник

Числовые и буквенные выражения

Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Значение выражения — это результат выполненных действий.

Чтение числовых выражений

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Для этого найдем значения каждого из них:

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

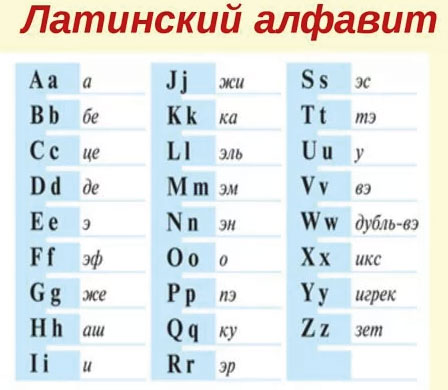
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Поделись с друзьями в социальных сетях:

Источник

Что такое сравнение? Примеры из художественной литературы

Сравнение — это сти­ли­сти­че­ский при­ём, осно­ван­ный на образ­ном сопоставлении
двух пред­ме­тов или состояний.

Сравнение — стилистическая фигура речи

Между неко­то­ры­ми пред­ме­та­ми и явле­ни­я­ми дей­стви­тель­но­сти мож­но уста­но­вить урав­ни­тель­ные отно­ше­ния, что явля­ет­ся слож­ной зада­чей для писа­те­ля. Но в этой необыч­но­сти и заклю­ча­ет­ся вся сила срав­не­ния как сти­ли­сти­че­ско­го при­е­ма в худо­же­ствен­ной речи. Сравнение сооб­ща­ет явле­нию или поня­тию то осве­ще­ние, такой отте­нок смыс­ла, какой наме­рен при­дать ему писатель.

Сравнение явля­ет­ся сти­ли­сти­че­ской фигу­рой речи, как и сле­ду­ю­щие образ­ные средства:

Использование срав­не­ния дела­ет вос­при­я­тие речи мно­го­пла­но­вым, вызы­ва­ет инте­рес у слу­ша­те­лей или чита­те­лей, помо­га­ет глуб­же про­ник­нуть в смысл выска­зы­ва­ния, рож­да­ет бога­тые образ­ные ассоциации.

Способы создания сравнения

Сравнения созда­ют­ся в худо­же­ствен­ной лите­ра­ту­ре несколь­ки­ми способами:

1. с помо­щью срав­ни­тель­ных сою­зов «как», «слов­но», «буд­то», «точ­но», «что» (чем):

2. фор­мой тво­ри­тель­но­го падежа:

Из пере­руб­лен­ной ста­рой берё­зы гра­дом лили­ся про­щаль­ные слё­зы. (Н.А. Некрасов)

Луга пре­вра­ти­лись в моря. Там пла­ва­ли не толь­ко дикие утки, но и пере­лет­ные лебе­ди. Последние ска­зоч­ным виде­ни­ем воз­ни­ка­ли на вод­ной гла­ди, и, зача­ро­ван­ный осле­пи­тель­ной кра­со­ты мира­жом, я сидел часа­ми, наблю­дая засле­зив­ши­ми­ся от вол­не­ния гла­за­ми, как эти явив­ши­е­ся как буд­то из сказ­ки суще­ства кру­жат вда­ли, а затем так же вне­зап­но, как и поло­же­но при­зра­кам, исче­за­ют (М. Алексеев).

3. фор­мой срав­ни­тель­ной сте­пе­ни при­ла­га­тель­но­го или наречия:

4. лек­си­че­ски — с помо­щью слов «подоб­ный», «похо­жий»:

Пирамидальные топо­ля похо­жи на тра­ур­ные кипа­ри­сы. (А.Серафимович).

Он был похож на вечер ясный… (М. Ю. Лермонтов).

Начинается гро­за с воз­душ­но­го стол­ба, обра­зу­ю­ще­го набу­ха­ю­щее белое обла­ко, похо­жее на кочан цвет­ной капу­сты (З. Ауст).

Родина подоб­на огром­но­му дере­ву, на кото­ром не сосчи­тать листьев. И все, что мы дела­ем доб­ро­го, при­бав­ля­ет ему сил (В. Песков).

Примеры сравнений из художественной литературы

С помо­щью срав­не­ния в лите­ра­ту­ре писа­тель рас­кры­ва­ет образ героя более ярко и пол­но. Читаем у клас­си­ка рус­ской лите­ра­ту­ры А.С. Пушкина:

Сравнения широ­ко при­ме­ня­ют­ся в опи­са­нии природы:

Посмотрим, как поэт Николай Заболоцкий мастер­ски постро­ил сти­хо­тво­ре­ние «Голос в теле­фоне» на срав­не­нии, что­бы ярко и образ­но создать настро­е­ние это­го про­из­ве­де­ния, более пол­но доне­сти до чита­те­ля свою поэ­ти­че­скую мысль.

Яркие, выра­зи­тель­ные срав­не­ния при­да­ют худо­же­ствен­ной речи осо­бую поэтичность.

Однако неко­то­рые срав­не­ния в резуль­та­те часто­го упо­треб­ле­ния при­об­ре­ли опре­де­лён­ную устой­чи­вость и вос­про­из­во­ди­мость, то есть пре­вра­ти­лись во фра­зео­ло­гиз­мы:

Видео «Тропы. Сравнение»

Источник

ГДЗ по математике, 2 класс, Моро М.И. Сравни выражения.

Сравни выражения.
1) Сумму чисел 8 и 9 и разность чисел 20 и 1.
2) Разность чисел 16 и 8 и разность чисел
16 и 10.

1) Запиши 3 любых двузначных числа. Умень-
ши каждое из них на 10.
2) Запиши 3 любых однозначных числа. Уве- ( Подробнее. )

Оля перепрыгнула через верёвочку 18 раз, а
Света — только 10 раз.
Поставь вопрос и реши задачу.

Кто сможет? Выполните деление:
( Подробнее. )

Троллейбус за время t прошел путь s. Какую скорость v приобрел он в конце пути и с каким ускорением а двигался, если начальная скорость ( Подробнее. )

Источник