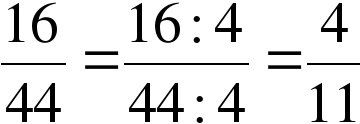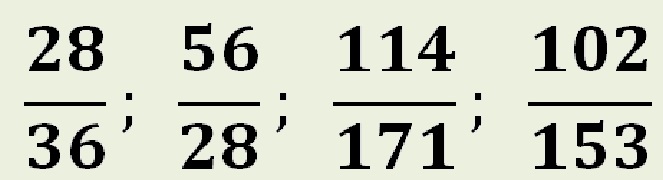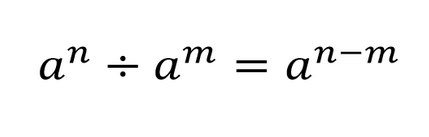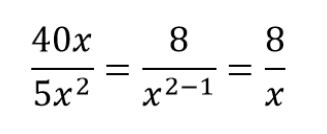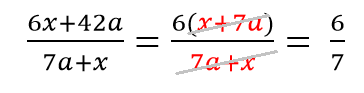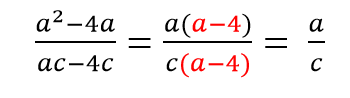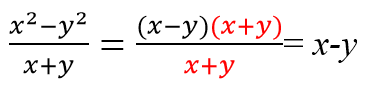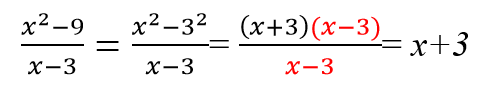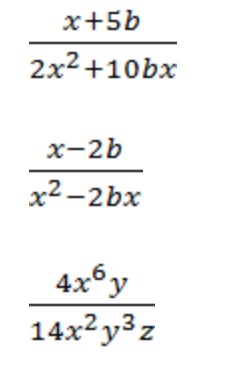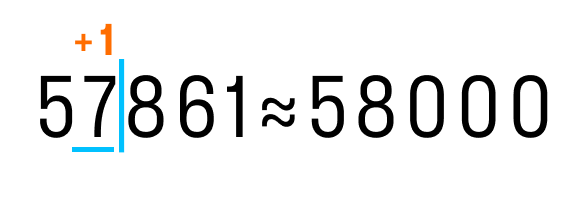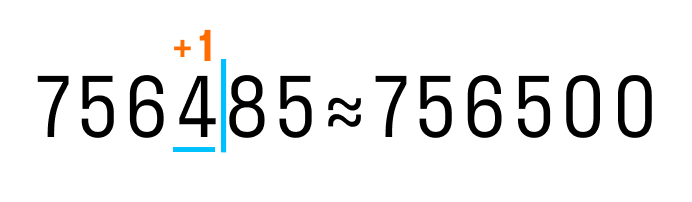Что значит сократить число

Сокращение дробей, правило и примеры сокращения дробей.

В этой статье мы подробно разберем, как проводится сокращение дробей. Сначала обговорим, что называют сокращением дроби. После этого поговорим о приведении сократимой дроби к несократимому виду. Дальше получим правило сокращения дробей и, наконец, рассмотрим примеры применения этого правила.

Навигация по странице.

Что значит сократить дробь?

Мы знаем, что обыкновенные дроби подразделяются на сократимые и несократимые дроби. По названиям можно догадаться, что сократимые дроби можно сократить, а несократимые – нельзя.

Что же значит сократить дробь? Сократить дробь – это значит разделить ее числитель и знаменатель на их положительный и отличный от единицы общий делитель. Понятно, что в результате сокращения дроби получается новая дробь с меньшим числителем и знаменателем, причем, в силу основного свойства дроби, полученная дробь равна исходной.

Приведение обыкновенных дробей к несократимому виду

Обычно конечной целью сокращения дроби является получение несократимой дроби, которая равна исходной сократимой дроби. Эта цель может быть достигнута, если провести сокращение исходной сократимой дроби на наибольший общий делитель ее числителя и знаменателя. В результате такого сокращения всегда получается несократимая дробь. Действительно, дробь является несократимой, так как из свойств НОД известно, что и — взаимно простые числа. Здесь же скажем, что наибольший общий делитель числителя и знаменателя дроби является наибольшим числом, на которое можно сократить эту дробь.

Итак, приведение обыкновенной дроби к несократимому виду заключается в делении числителя и знаменателя исходной сократимой дроби на их НОД.

Заметим, что под фразой «сократите дробь» часто подразумевают приведение исходной дроби именно к несократимому виду. Другими словами, сокращением дроби очень часто называют деление числителя и знаменателя на их наибольший общий делитель (а не на любой их общий делитель).

Как сократить дробь? Правило и примеры сокращения дробей

Осталось лишь разобрать правило сокращения дробей, которое и объясняет, как сократить данную дробь.

Правило сокращения дробей состоит из двух шагов:

Разберем пример сокращения дроби по озвученному правилу.

Источник

Сокращение дроби.

Мы уже познакомились с основным свойством дроби (см. статью здесь). И знаем, как получить дробь, равную данной. Но сегодня мы поговорим о ДЕЛЕНИИ дроби на одно и то же число.

Деление числителя и знаменателя на одно и то же натуральное число называется СОКРАЩЕНИЕМ ДРОБИ. Но при этом – дроби остаются РАВНЫМИ.

Как сокращать дроби? Будем разбираться.

Итак, сокращение дроби – это действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Сокращение дроби выполняют для того, чтобы ее упростить.

Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же натуральное число, которое будет называться общим делителем.

Например, дана дробь 2/6.

На какие числа можно разделить 2? 2 делится на 1, 2. На какие числа можно разделить 6? 6 делится на 1, 2, 3, 6.

Но, мы знаем, что если дробь разделить на 1, то будет та же самая дробь. Поэтому на 1 не сокращают!

Теперь посмотрим на делители чисел 2 и 6. Сравним их:

Найдем одинаковые делители – это только число 2. Значит, мы можем разделить числитель и знаменатель нашей дроби только на 2.

Дробь 1/3 сократить нельзя.

Посмотрим на дробь 16/44. 16 делится на 2, 4, 8, 16. 44 делится на 2, 4, 11, 44. Одинаковые делители – 2, 4.

Разделим дробь на 2 — 16:2/44:2 = 8/22. Эту дробь можно еще сократить на 2. 8/22 = 8:2/22:2 = 4/11. Это очень долго, поэтому будем сокращать сразу на 4.

Дробь 4/11 сократить нельзя.

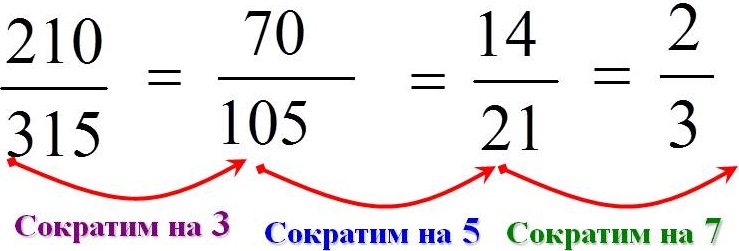
Рассмотрим дробь с большими числами: 210/315.

210 делится на 2, 3, 5, 7, 10, 30, 70, 105, 210.

315 делится на 3, 5, 7, 9, 15, 21, 63, 105, 315.

Общие делители: 3, 5, 7, 105. Будем сокращать дробь постепенно:

Мы видим, что если сокращать поочереди на все общие числители, начиная с меньшего, очень долго. Поэтому для удобства принято сокращать дробь сразу на больший числитель. Т.е. 210/315 = 210:105 / 315:105 = 2/3 Полученную дробь 2/3 сократить нельзя.

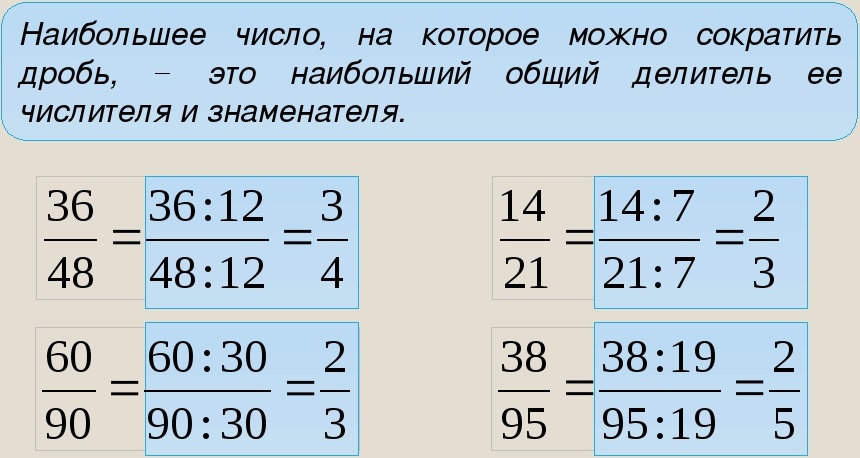
Наибольший общий делитель называют сокращенно — НОД.

Бывают случаи, когда общего делителя нет. Например, у дробей 3/59, 6/31, 11/23 и т.д. Тогда говорят о том, что эти дроби не подлежат сокращению.

Дроби, которые сократить НЕЛЬЗЯ называются НЕСОКРАТИМЫМИ, а числитель и знаменатель называют ВЗАИМНО-ПРОСТЫМИ.

Т.е. наша задача превратить любую дробь в несократимую. Итак, мы познакомились в двумя способами сокращения дробей:

Проверка: 28/36 – наибольший общий делитель (НОД) = 4, значит 28:4/36:4 = 7/9;

56/28 – НОД = 28, значит, 56:28/28:28 = 2/1 = 2;

114/171 – НОД = 57, значит, 114:57/171:57 = 2/3;

102/153 – НОД = 51, значит, 102:51/153:51 = 2/3.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 75

Источник

Как сокращать алгебраические дроби?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.

Сокращение дробей с буквами и степенями проходит в три этапа:

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

❌ Так нельзя	✅ Так можно

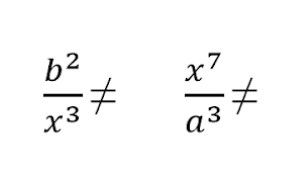Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Получаем сокращенную дробь.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Пример 1.

Пример 2.

Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Примеры сокращения дробей с помощью формул сокращенного умножения:

Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

Источник

Сокращение дробей: правила и примеры

Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Что такое «сокращение дробей»

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

Приведение дробей к несократимому виду

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

6 24 = 6 ÷ 6 24 ÷ 6 = 1 4

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

182 195 = 182 ÷ 13 195 ÷ 13 = 14 15

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Для этого представим исходную дробь в виде:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44

20 44 = 20 ÷ 2 44 ÷ 2 = 10 22

Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:

Источник

Правильное округление чисел

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Примерчики

Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

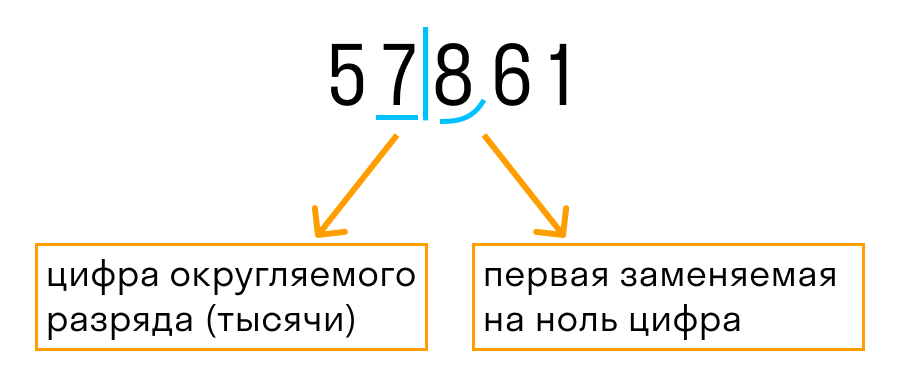
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

Округление десятичных дробей

Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

Разряды дробной части:

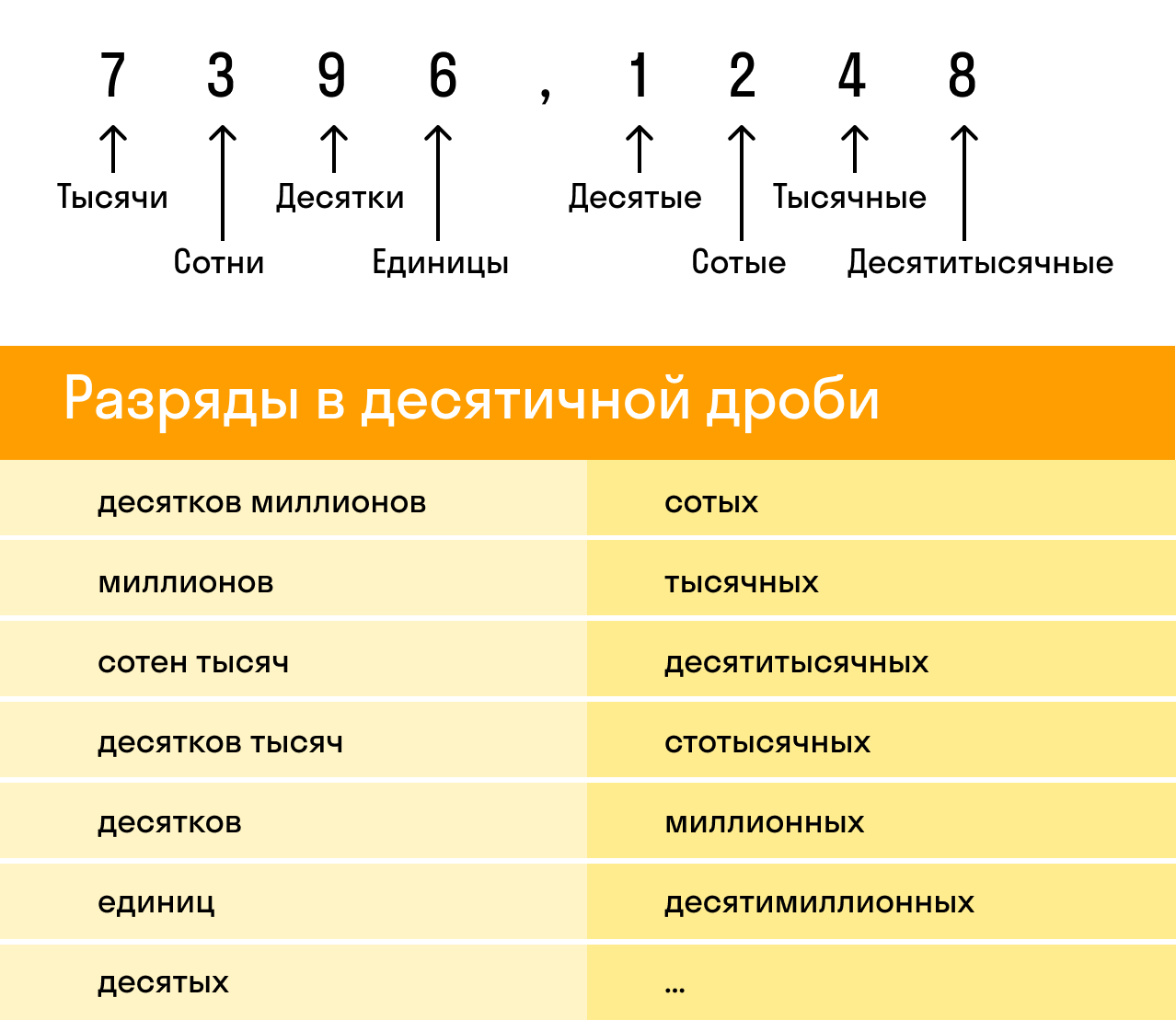
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.

Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Пример 1

256,43 ≈ 256,4 — округление до десятых;

4,578 ≈ 4,58 — округление до сотых;

17,935 ≈ 18 — округление до целых.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.

Пример 2

79,7 ≈ 80 — округление до десятков;

0,099 ≈ 0,10 — округление до сотых.

Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.

Источник