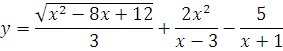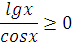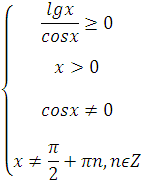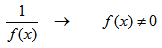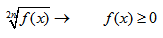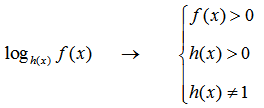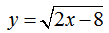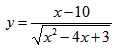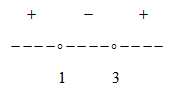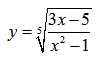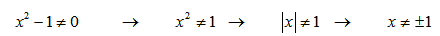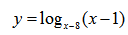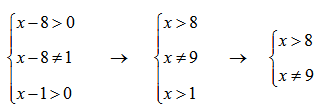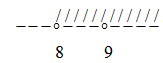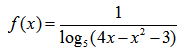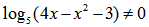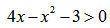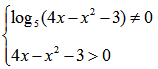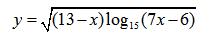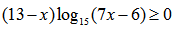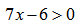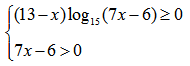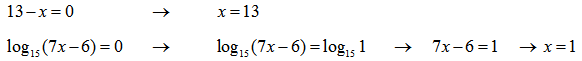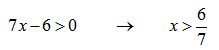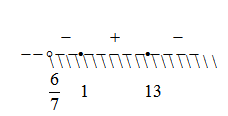Что значит область определения функции заданной формулой
В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).
Общие сведения
Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».
Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.
Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.
Основные понятия
Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.
Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.
Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.
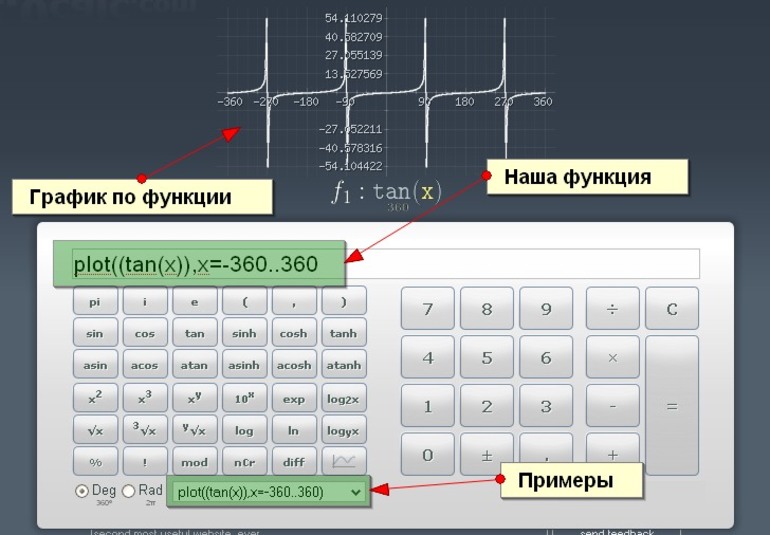
Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.
Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.
Типы функций
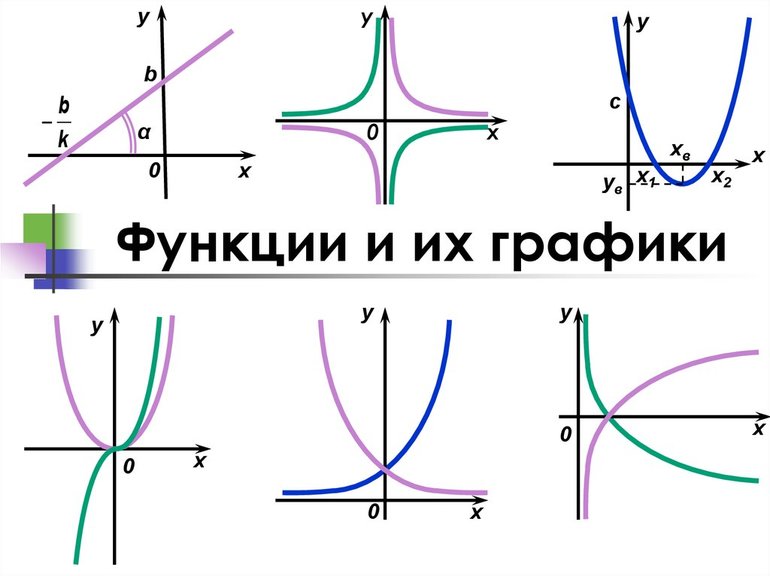
Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.
Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.
Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.
К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.
Правильное обозначение
Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.
Следует руководствоваться такими правилами:
Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.
Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].
Алгоритмы определения
Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.
Если функция является дробной, то следует использовать следующий алгоритм:
Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).
Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.
Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.
Другие методы
Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.
Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.
В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).
После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.
Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.
Примеры решения
Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.
С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.
Для линейного вида
Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:
В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.
Дробные и иррациональные
Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).
Решается задача таким способом:
В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения.
Для решения квадратного уравнения следует применить такой алгоритм:
Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).
Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.
Область определения функции. Примеры.
Что такое область определения функции? Как её находить? Эти вопросы частенько представляются сложными и непонятными. Хотя, на самом деле, всё чрезвычайно просто. В чём вы сможете убедиться лично, прочитав эту страничку. Поехали?)
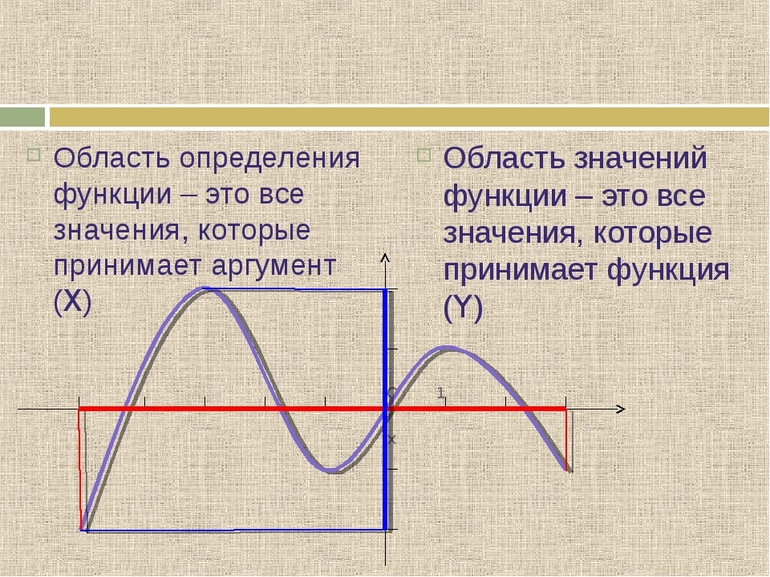
В элементарном понятии функции фигурируют две величины. Независимая переменная (аргумент) x и зависимая переменная (функция) y.
Все допустимые (разрешённые) значения аргумента x и есть область определения функции. И всё.
Достаточно разобраться в этой нехитрой фразе, как всё сразу становится на свои места.
Что такое «допустимые значения»? Говоря по-простому, это те значения икса, для которых можно посчитать игрек. В принципе. Например, дана функция:
Разумеется, функция может быть такой замороченной, что и не посчитаешь ничего, да. Это не страшно. Нам ведь не считать надо, а область определения найти). Чуть ниже мы научимся легко и элегантно расправляться с любыми функциями. Даже самыми злыми.)
Слова «можно посчитать в принципе«, «принципиальные запреты» я не зря употребил. Вот вам другой простенький пример. Дана функция:
Область определения любой функции устанавливают:
1. Математика. Это законы и правила, которые всегда должны выполняться. Эти правила не зависят от нашего желания и вида задания. Они работают всегда. Область определения по этим правилам иногда называют «естественной».
2. Люди. Это дополнительные ограничения на область определения функции, которые могут быть (а могут и не быть) в любом конкретном задании и зависят исключительно от составителя задания.
Самым важным является первый пункт. С него и начнём.
Как найти область определения функции?
На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.
На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.
Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет.
Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю:
До 9-го класса включительно:
1. Деление. Нельзя делить на ноль.
2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.
В выпускных классах и ВУЗах:
3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0.
4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.
Это, практически, весь набор потенциально опасных операций. Можно запомнить, правда?)
Вот и всё, что надо знать, чтобы найти область определения любой функции.
Теперь самое время применить эти знания в деле. Найдём область определения самой первой функции. Не перебором, а вполне научно):
D(f)=(-∞;+∞)
Как видите, в этом примере второй этап вовсе не понадобился. Бывает. Хорошая функция.)
Определяем иксы, которые не приводят к запретному действию, т.е. делению на ноль. Собственно, к делению на ноль приводит лишь одно значение икса: x=0. Следовательно, все остальные значения безопасны. Областью определения функции будут все действительные числа, кроме нуля. В краткой записи:
D(f)=(-∞;0) ∪ (0; +∞)
Это были совсем простые примеры. Для знакомства). Переходим к более солидным заданиям.
Найти область определения функции:
Что, внушает?) Ничего не боимся и работаем по схеме.
Выполняем первый этап: осматриваем функцию, на предмет потенциально опасных операций.
Внимание! Мы ничего не решаем! Не упрощаем, не складываем дроби, не раскладываем на множители, не извлекаем корни, ни-че-го! Мы именно осматриваем функцию. Любые преобразования могут изменить область определения функции и мы получим неверный ответ.
Сразу же выполняем и второй этап: то, что найдём в процессе осмотра, будем записывать, чтобы не забыть.)
Итак, в первом слагаемом видим квадратный корень из выражения с иксом. Это потенциально опасная операция. Под корнем, при каких-то иксах, может оказаться отрицательное число. Обезопасим себя вот такой записью (второй этап):
Уловили? Квадратный корень извлекается только из положительных чисел и нуля. Всё подкоренное выражение должно быть больше, либо равно нулю. Не икс, а всё подкоренное выражение, целиком. Прошу заметить: в этой записи уже нет знака корня! А то так и норовят его написать. Корень нам не нужен, нас интересует только подкоренное выражение. Так, с корнем разобрались, идём дальше.
Второе слагаемое. В нём есть деление на выражение с иксом. Знаменатель (весь знаменатель, целиком!) не может быть равен нулю. Записываем (второй этап):
х-3 ≠ 0
Так, соломки подстелили, идём дальше. В третьем слагаемом опять есть деление. Записываем:
х+1 ≠ 0
Ну, всё, функция кончилась.) Теперь сводим все наши записи в систему неравенств:
Система необходима, так как все наши условия должны выполняться одновременно.
Осталось решить эту систему. В ответе получится как раз область определения этой функции. Ответ будет такой:
Как видим, функция может быть каким угодно монстром. Но в процессе осмотра и соответствующих записей мы получаем системку неравенств, которая вполне решаема.
Так поступаем при нахождении области определения любой функции.
Не знаете, как решать системы!? Ну, это вопрос не к функциям. Имейте в виду: задание как найти область определения функции почти всегда заканчивается решением системы неравенств. Как решать квадратные неравенства можно посмотреть по ссылке. Там, кстати, решено с пояснениями именно наше квадратное неравенство. Чисто случайно. )
Последовательный осмотр и запись системы неравенств обычно особого труда не составляют. Хуже, когда потенциально опасные операции ещё и наслаиваются друг на друга. Здесь требуется пристальное внимание, чтобы чего не упустить. Например:
Найти область определения функции:
На первом этапе замечаем квадратный корень. Сразу пишем условие для всего подкоренного выражения:
Так, квадратный корень обезопасили. Но двигаться дальше ещё рано. Внутри корня есть ещё две потенциально опасные операции! Логарифм и деление. Для логарифма записываем:
Для деления записываем:
Вот теперь первое слагаемое разобрано по косточкам. Можно двигаться дальше. Для тангенса нужно записать:
Вот и всё. Сводим все наши записи в систему:
Повторю алгоритм ещё раз:
1. Работаем с исходной функцией! Ничего не упрощаем и не преобразовываем! Это всё делаем (если надо будет) после нахождения области определения.
2. Внимательно осматриваем функцию на предмет потенциально опасных операций.
3. В процессе осмотра записываем в систему неравенства, которые обеспечивают допустимость опасных операций.
4. Решаем систему неравенств и записываем ответ.
Самые внимательные, наверняка, почувствовали схожесть этого процесса с нахождением области допустимых значений (ОДЗ).
Ну, что тут сказать. Только респект.) Да! Естественная область определения функции (о которой здесь идёт речь) совпадает с ОДЗ выражений, входящих в функцию. Соответственно, и ищутся они по одним и тем же правилам.
А сейчас рассмотрим не совсем естественную область определения.)
Дополнительные ограничения на область определения функции.
Здесь речь пойдёт об ограничениях, которые накладываются заданием. Т.е. в задании присутствуют какие-то дополнительные условия, которые придумал составитель. Или ограничения выплывают из самого способа задания функции.
Например, такое задание:
Найти область определения функции:
на множестве положительных чисел.
Естественную область определения этой функции мы нашли выше. Эта область:
А теперь учитываем дополнительные ограничения. Слова «на множестве положительных чисел» означают, что иксы могут быть только положительные. Вместо этих слов может быть задано условие «где x>0″, или «где х ∈ (0; +∞)». Если наложить это ограничение на ответ, получим новую область определения:
D(f)=(0; 2] ∪ [6; +∞)
Всё предыдущее относилось к области определения аналитически заданных функций. Это самые популярные функции. Но существуют и другие способы задания функции. Они менее привычны и могут поставить в тупик. Во избежание таких фокусов, кратенько пробежимся по D(f) для функций, заданных НЕ аналитически.
В табличном способе областью определения функций будут только те значения икса, которые даны в таблице. Других иксов для такой функции просто не существует. Разумеется, если в задании будут дополнительные ограничения на D(f), их надо будет учесть. Но основным источником информации будет таблица.
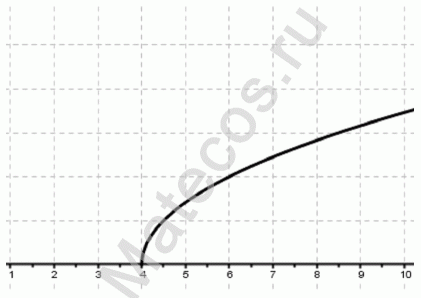
Найти область определения функции у=f(x):
При значении х=+6, на графике отмечена закрашенная точка. Это значит, что при х=+6 функция существует. Этот икс необходимо включить в D(f). Вот и всё. Ответ:
В словесном способе задания функции нужно внимательно читать условие и находить там ограничения на иксы. Иногда глаза ищут формулы, а слова свистят мимо сознания да. ) Пример из предыдущего урока:
Функция задана условием: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х.
Здесь надо заметить, что речь идёт только о натуральных значениях икса. Тогда и D(f) мгновенно записывается:
D(f): х ∈ N
Открою маленький секрет. Иногда функция, для которой надо найти область определения, выглядит просто устрашающе. Хочется побледнеть и заплакать.) Но стоит записать систему неравенств. И, вдруг, системка оказывается элементарной! Причём, частенько, чем ужаснее функция, тем проще система.
Как найти область определения функции?
 |
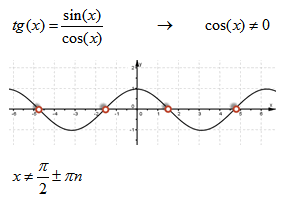 | на графике тангенса | 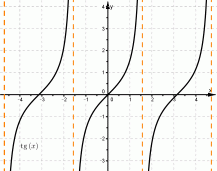 |
Для котангенса:
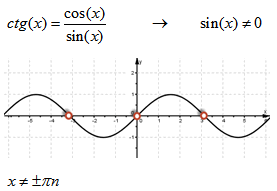 | на графике котангенса | 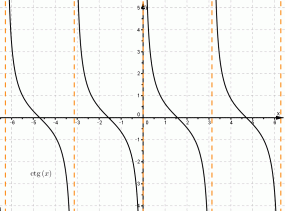 |
4. Обратные тригонометрические функции.
| Арксинус | Арккосинус | Арктангенс, Арккотангенс |
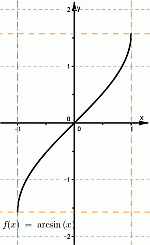 | 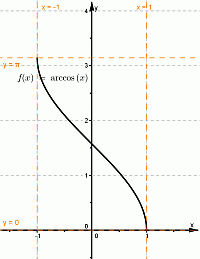 | 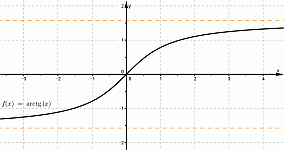 |
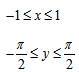
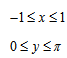
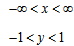
| Пример 1 | Пример 2 |
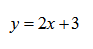 | 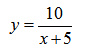 |
| Пример 3 | Пример 4 |
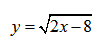 | 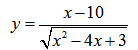 |
| Пример 5 | Пример 6 |
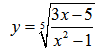 | 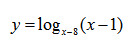 |
| Пример 7 | Пример 8 |
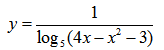 | 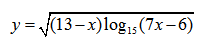 |
| Пример 9 | Пример 10 |
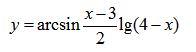 | 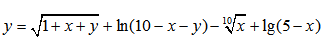 |
| Пример 11 | Пример 12 |
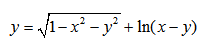 | 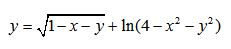 |
| Пример 13 | Пример 14 |
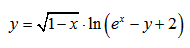 |
| Пример 15 | Пример 16 |
Пример нахождения области определения функции №1
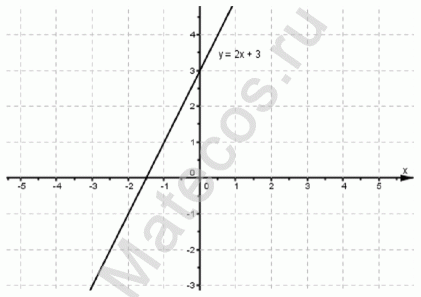
Нахождение области определения любой линейной функции, т.е. функции первой степени:
y = 2x + 3 — уравнение задает прямую на плоскости.
Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?
Попробуем подставить значение х=0
Попробуем подставить значение х=10
Попробуем подставить значение х=-10
Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.
Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.
Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R
Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)
Для любой функции вида y = ax + b областью определения является множество действительных чисел.
Пример нахождения области определения функции №2
Задана функция вида:
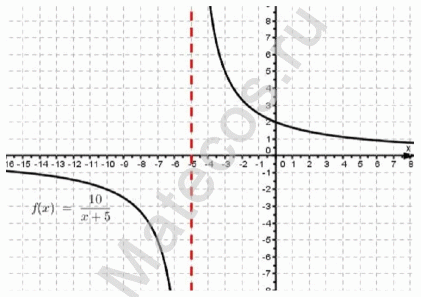
y = 10/(x + 5) — уравнение гиперболы
Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не
обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.
Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.
Для наглядности изобразим графически:
Формы записи ответа: D(f)=R\ <-5>или D(f)=(-∞;-5) ∪ (-5;+∞) или x ∈ R\ <-5>или x ∈ (-∞;-5) ∪ (-5;+∞)
Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.
Пример нахождения области определения функции №3
Рассмотрим пример нахождения области определения функции с корнем четной степени:
Решим простое неравенство:
При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.
Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.
Пример нахождения области определения функции №4
Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)
Решим строгое неравенство методом интервалов:
Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)
Пример нахождения области определения функции №5
Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.
Пример нахождения области определения функции №6
Рассмотрим пример нахождения области определения логарифма:
Простенький пример на область определения логарифмической функции.
Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:
Покажем на числовой прямой:
Пример нахождения области определения функции №7
Задана функция вида:
1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):
Второе ограничение — подлогарифмическое выражение положительно:
Т.е. для определения области определения заданной функции необходимо решить систему:
Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.
Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.
Пример нахождения области определения функции №8
Рассмотрим следующий пример:
Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:
Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:
Таким образом для определения области определения исходной функции необходимо решить систему неравенств:
Каждое из неравенств решим по отдельности.
Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.
Выносим на координатную прямую:
Объясню как расставлены знаки в каждом из интервалов:
Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.
Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с » — » на » + «.