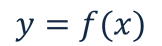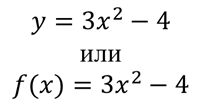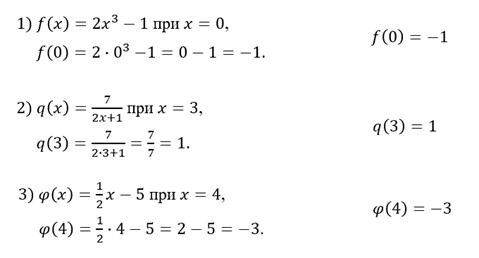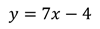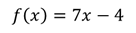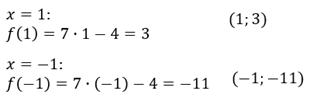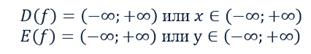Что значит область определения функции и область значения функции

Функция: область определения и область значений функций

Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.

Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).

2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)

Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).

2. у=х^2. (наз. парабола)

4. у= √ х. (наз. ветвь параболы)

Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.

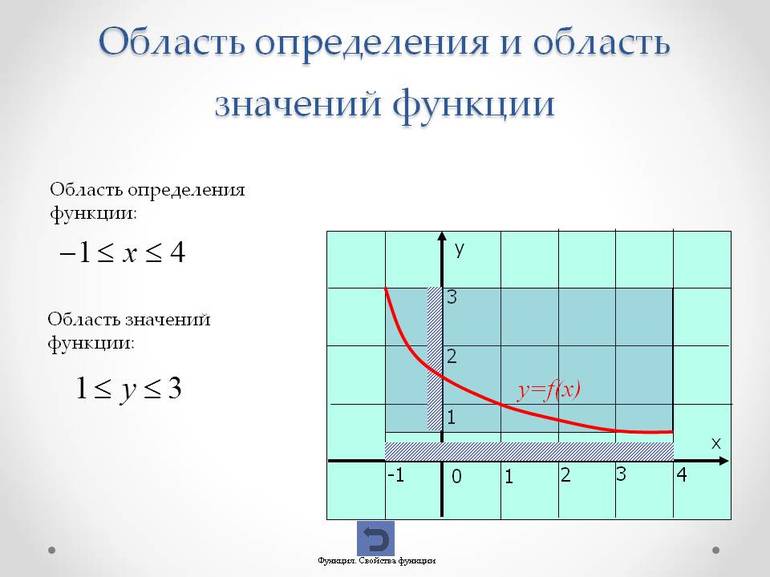
Область определения функции

Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).

Рассмотрим D (у) для 1.,2.,3.,4.

1. D (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.

2. D (у)= ( ∞; +∞)//всё мн-во действит.чисел

3. D (у)= ( ∞; +∞)//всё мн-во действит.чисел

4. D (у)= [0; +∞)// мн-во неотрицат.чисел

Зависимая переменная (кот. мы обозначаем у ) имеет название значение функции.

Область значения функции

Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).

Рассмотрим Е (у) для 1.,2.,3.,4.

1. Е (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.

2. Е (у)= [0; +∞)// мн-во неотрицат.чисел

3. Е (у)=( ∞; +∞)//всё мн-во действит.чисел

4. Е (у)= [0; +∞)// мн-во неотрицат.чисел

Рассмотрим примеры подробнее

1) Постановка задачи. Найти функции у= 4х/(3+х)

1. Найдем D (у)//т.е. какие значения может принимать х. для этого найдем ОДЗ(область допустимых значений дроби)

значит D (у) данной функции ( ∞; 3) и (3;+∞)// всё множество действительных чисел, кроме 3.

2. Найдем Е (у)//т.е. какие значения может принимать у, при всех возможных х

решаем уравнение вида 4х/(3+х)=А, где А є Е (у)

значит Е (у) данной функции ( ∞; 4) и (4;+∞)// всё множество действительных чисел, кроме 4.

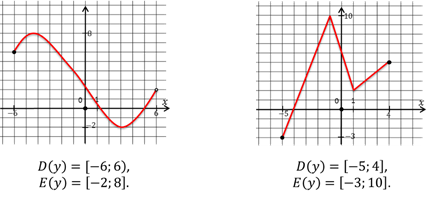
2) Постановка задачи. Найти D (у)и Е (у) функции, изображенной на графике

Область определения(значения х) смотрим по оси х- это промежуток [ 4; 7],

Областью значения(значения у) смотрим по оси у- это промежуток [ 4; 4].

Источник

Функция. Область определения и область значений функции

Урок 1. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Функция. Область определения и область значений функции»

Зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение y, называют функцией.

В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции.

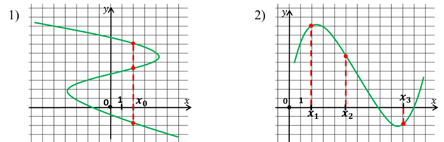
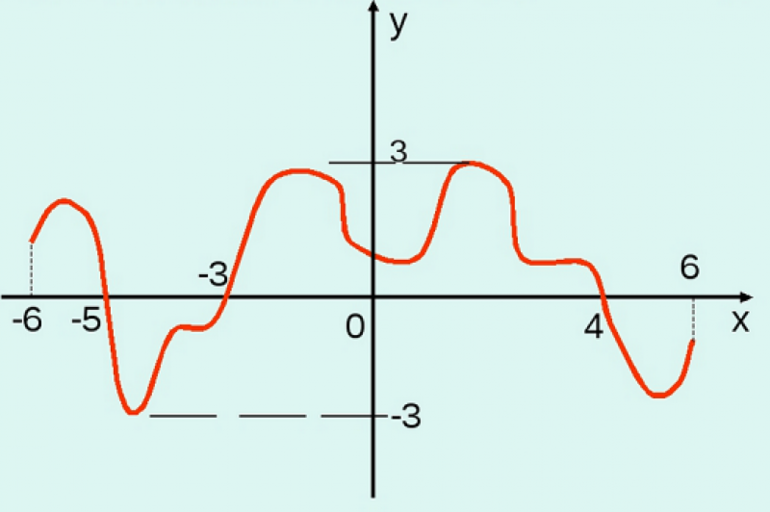
Рассмотрим первый график. Видим, что одному значению x может соответствовать несколько значений y. Значит, данная зависимость не является функцией.

Обратимся ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них соответствует только одно значение функции. Можно сказать, что эта зависимость является функцией.

В общем виде любую функцию можно записать так:

Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.

Вы заметили, что в этом задании функции названы разными буквами. Действительно, функцию можно называть любой буквой латинского алфавита.

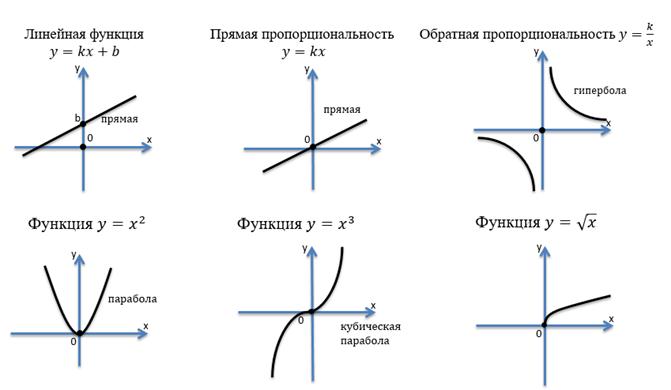
Ранее вами были изучены несколько важных функций. Вспомним их.

Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.

Можно записать её в таком виде:

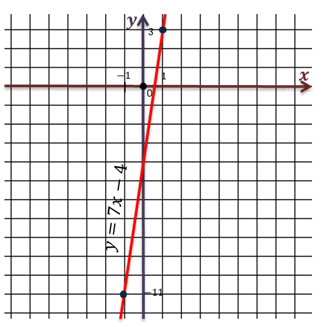
Это линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.

Получаем точки с координатами (1;3) и (-1;-11).

Проведём прямую через полученные точки.

Мы изобразили график функции.

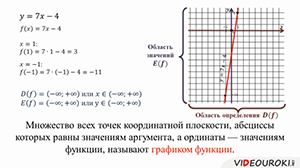
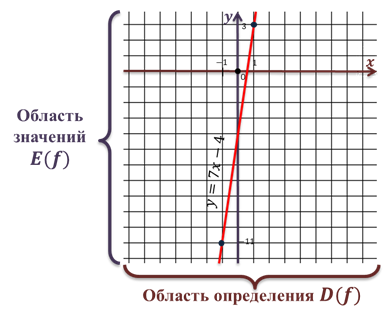
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.

Все значения аргумента, т.е. переменной x образуют область определения функции, а все значения зависимой переменной, т.е. y, — область значений функции.

В данном случае x и y могут быть любыми числами, т.е. областью определения и областью значений является множество всех действительных чисел.

Потренируемся находить область определения и область значений функции по её графику.

Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.

Источник

Определение числовой функции. Область определения функции. Область значения функции.

Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.

Определение функции.

Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.

х — называется независимой переменной или аргументом.

y – называется зависимой переменной или значением функции.

Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.

Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.

Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.

В тех диапазонах в которых существует переменная х называется областью определения функции.

В тех диапазонах в которых существует переменная y называется областью значения функции.

Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.

Разберём пример №1:

Найдите область определения и область значения числовой функции y=x 2

Вместо переменной x мы можем брать любые числа и просчитать переменную y.

По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).

Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).

Разберём пример №2:

Найдите область определения и область значения числовой функции y=x+1?

Вместо переменной x мы можем брать любые числа и просчитать переменную y.

По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).

Источник

Область определения функции

Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.

В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.

Понятие и обозначение области определения функции

Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.

По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:

Используя это определение, охарактеризуем нужное нам понятие более четко:

Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.

Как найти области определения для основных элементарных функций

Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y = x 2 и т.д., а их области определения указываются в качестве основных свойств.

В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.

Область определения постоянной функции

Область определения функции с корнем

Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.

Область определения степенной функции

Перечислим возможные варианты.

Поясним нашу мысль несколькими примерами.

Область определения показательной функции

Область определения логарифмической функции

Область определения тригонометрических функций

Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.

Область определения тригонометрических функций

К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.

Области определения основных функций в табличном виде

Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.

y = sin x y = cos x y = t g x y = c t g x

y = a r c sin x y = a r c cos x y = a r c t g x y = a r c c t g x

Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания. Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.

Источник

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Источник

• ← Что значит область определения функции заданной формулой
• Что значит область определения функции симметрична относительно нуля →