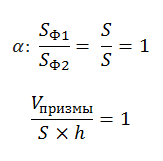Что значит найти объем

Как найти объём геометрических фигур

Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м 3 ).

Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.

Содержание:

Как найти объем трехмерных объектов

Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.

Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м 3 /1000000 = 0,004256 м 3

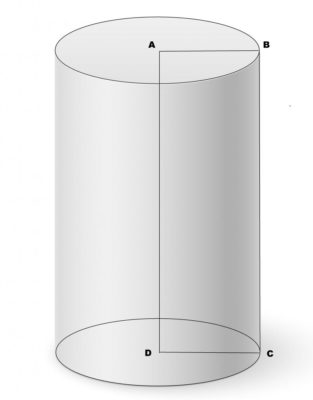
Как найти объем для фигур цилиндрической формы

Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.

Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.

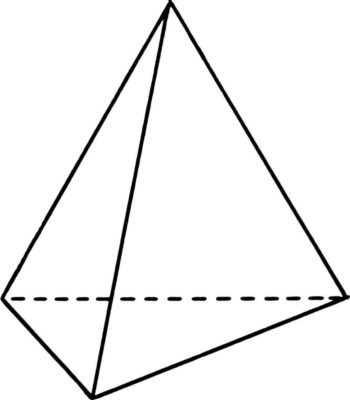
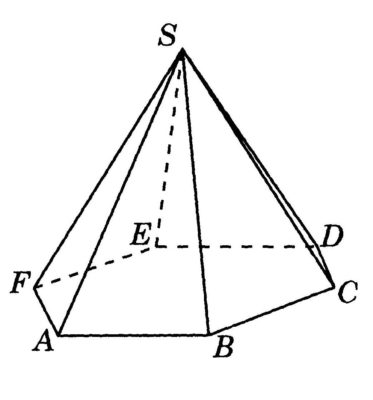
Как рассчитать объем треугольной пирамиды

Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.

Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.

В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.

Как посчитать объем куба

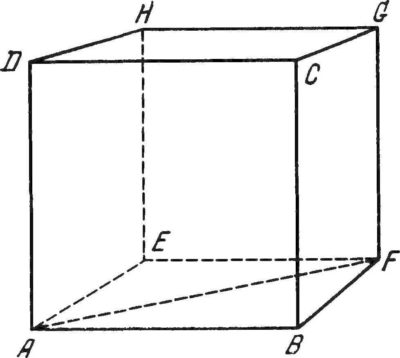
Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.

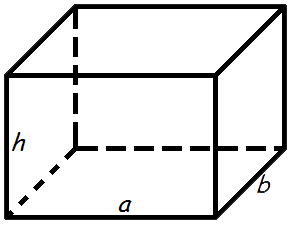
Как найти объем прямоугольного параллелепипеда

Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:

Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см 3

Советы по измерению:

Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.

Как найти объем цилиндра

Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:

Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:

3,14 * 2 см 2 * 5 см = 62.831853071796 = 63см 3

Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.

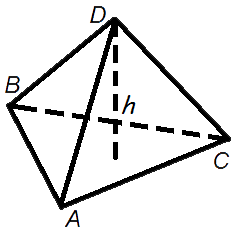
Как найти объем пирамиды

фото 6 — посчитать объём

Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:

Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:

V = 3 * 2 = 2 см 3 ‒ это и будет являться объемом искомой геометрической фигуры.

Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.

Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.

Источник

Объемы геометрических тел

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

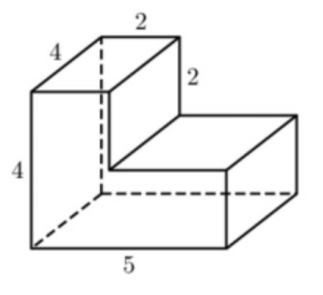
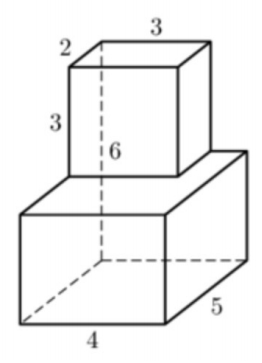
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

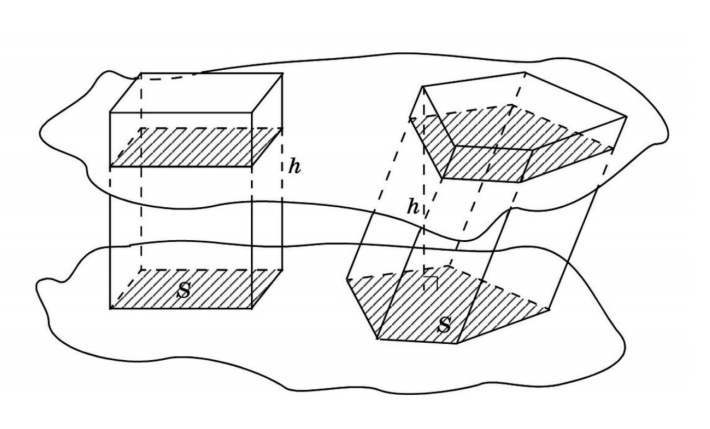
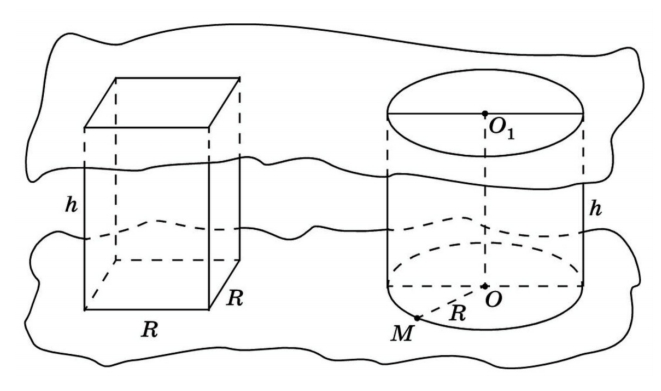
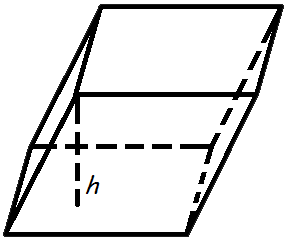
Объем призмы

В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

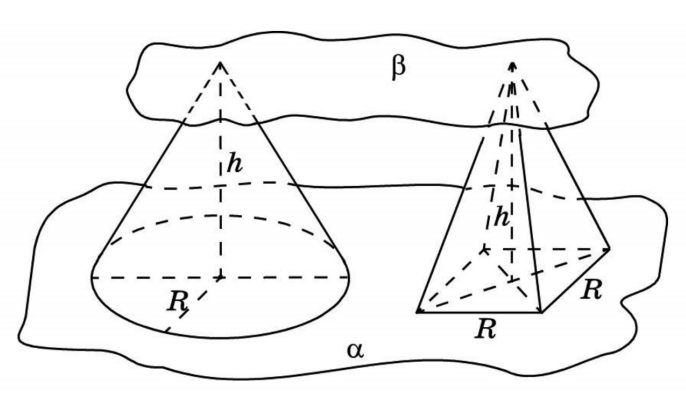
Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

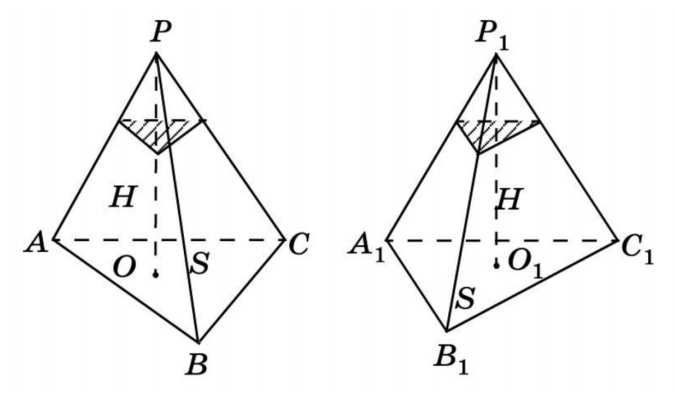
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

Объем цилиндра

Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Объем конуса

Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Источник

Формулы объема геометрических фигур

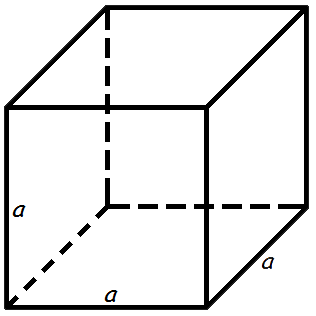
Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

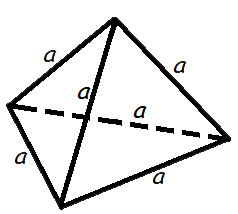
Объем правильного тетраэдра

Формула объема правильного тетраэдра:

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Перечень вопросов, рассматриваемых на уроке:

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

— равные тела имеют равные объёмы;

— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см 3 ). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n 3

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см 3 ). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём прямоугольного параллелепипеда

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

По доказанному в первом случае, левая часть неравенства представляет собой объём V_n прямоугольного параллелепипеда P_n с измерениями a_n, b_n, c_n, а правая часть – это объём V_n’ прямоугольного параллелепипеда P_n’ с измерениями a_n’, b_n’, c_n’. Так как параллелепипед P содержит в себе параллелепипед P_n, а сам содержится в параллелепипеде P_n’, то объём V параллелепипеда P заключён между V_n, = a_nb_nc_n и V_n’= a_n’b_n’c_n’. Будем неограниченно увеличивать n. Тогда 1/10 n будет становиться сколь угодно малым, и поэтому произведение a_n’b_n’c_n’ будет сколь угодно мало отличаться от числа, выраженного произведением a_nb_nc_n. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением a_nb_nc_n, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см 3

№2.

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Источник

Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.

Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …

Формула расчёта объёма прямоугольной ёмкости

V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).

Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.

Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →

Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …

Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →

Формулы расчёта объёма цилиндра:

Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.

Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).

Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.

Единицы измерения объёма

Вначале кратко ознакомимся с единицами измерения объёма как таковыми.

Официальной единицей измерения объема в системе СИ является м 3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм 3 — кубические дециметры, см 3 — кубические сантиметры, литры …

Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.

Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C

Соотношение единиц объёма

1 м3 = 1000 дм 3 = 1 000 000 см 3 = 1 000 000 000 мм 3 = 1000 литров
1 литр = 0,001 м 3 = 1 дм 3 = 1 000 см 3 = 1 000 000 мм 3

Конвертер единиц объёма

Конвертация кубических метров ( м 3 ) в кубические сантиметры ( см 3 ) и литры

Конвертация литров в метры кубические ( м 3 ) и кубические сантиметры ( см 3 )

Конвертация кубических сантиметров ( см 3 ) в кубические метры ( м 3 ) и литры

Заключение

Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта. Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.

Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

1 комментарий к “Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …”

Быстро и удобно если много объёмов

Оставьте комментарий Отменить ответ

Поделись с друзьями 🙂

Рубрики сайта

Публикации

Публикации

Поиск по сайту

Все материалы сайта защищены Законом «Об авторском праве и смежных правах». Сайт – vodamama.com является общедоступным и работает в рамках и в соответствии с действующим законодательством Украины.

Администрация ресурса может не разделять мнение автора. При подготовке материалов информация берётся из общедоступных источников и специальной проверки на достоверность не проходит.

Администрация сайта радикально негативно относится к нарушениям авторских или каких либо других имущественных прав. Поэтому, если Вы вдруг обнаружили, что на страницах нашего сайта нарушены, какие либо авторские или имущественные права, просим вас незамедлительно, воспользовавшись формой обратной связи, сообщить нам про это. После получения подтверждения нарушения мы незамедлительно устраним его.

Источник