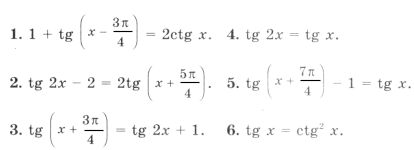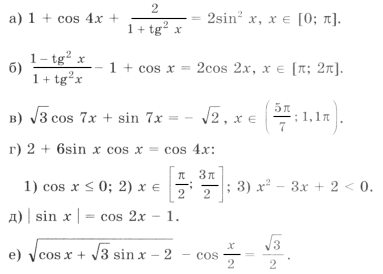Что значит найти объединение в тригонометрии
Отбор корней в тригонометрическом уравнении из ЕГЭ по математике
Одно из заданий второй части ЕГЭ по математике — решение тригонометрических уравнений с корнем. Основная его сложность в том, что нужно уметь не только упрощать выражения и находить ответ, но и проводить отбор корней. Как это сделать, мы разберем в статье.
Что такое тригонометрическое уравнение
Тригонометрическое уравнение содержит в себе функцию синуса, косинуса, тангенса или котангенса. Решение без отбора корней происходит по следующим формулам:
sinx = a при |a| ≤ 1 → x = (-1) n arcsina + πn;
cosx = a при |a| ≤ 1 → x = ± arccosa + 2πn;
tgx = b при b — любое число → x = arctgb + πn;
сtgx = b при b — любое число → x = arcсtgb + πn.
Отбор
Прежде чем изучить методы отбора корней, решим один несложный пример.
Первое слагаемое распишем по формуле косинуса двойного угла:
Приведем однородные слагаемые:
Пусть cosx = t, где |t| ≤ 1
x 1 = 3+ 1 2 2 = 4 4 =1
x 2 = 3- 1 2 2 = 2 4 = 1 2
Возвращаемся к исходной переменной и получаем:
cosx = 1 → x = 2πn, n ∈ Z
cosx = ½ → x = ± π/3 + 2πk, k ∈ Z
Области допустимых значений нет, поэтому оба значения используем при решении пункта «б».
Теперь проведем отбор корней разными способами.
Арифметический
Для решения нужно перебирать все значения целочисленного параметра и считать корни. Разберем на примере cosx = 1.
Далее то же самое нужно сделать с остальными корнями. Тогда вы получите ответ.
Алгебраический
Чтобы отобрать корни, нужно решить неравенства относительно известного целочисленного параметра. Рассмотрим на примере первого значения.
Делим все части неравенства на «2π»:
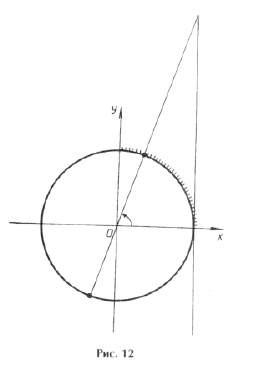
Геометрический
Рисуем единичную окружность, наносим на нее числа из области и корни. После определяем, попадают ли они в промежуток. Отсчет промежутка происходит против часовой стрелки!
Функционально-графический
Как видно по рисунку, у нас получаются те же корни, что и в предыдущем методе.
Теперь вы знаете основные способы отбора корней в тригонометрических уравнениях. Это поможет вам правильно решать задания из второй части. Дома вам сложно практиковаться, не хватает помощи учителя? Тогда записывайтесь на курсы подготовки к ЕГЭ в центре «Уникум» при Российском университете дружбы народов. Центр предлагает не только полезные уроки с экспертами ЕГЭ, но и доступ к учебному порталу. На нем вы сможете делать домашние задания, решать пробные варианты экзамена и изучать полезные материалы. Форматы курсов разные — очный и дистанционный.
Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях
Практика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
2sin x sin 2x – 2sin 2 x = 0,
Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1( · ).
Ответ:
Пример 2. tg x + tg 2x – tg 3x = 0.
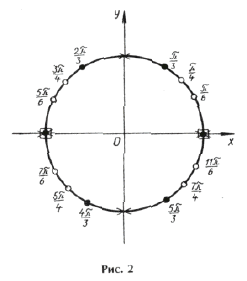
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1( o ) входит в серию x3( · ), поэтому ответ можно записать одной формулой:
Пример 3.
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
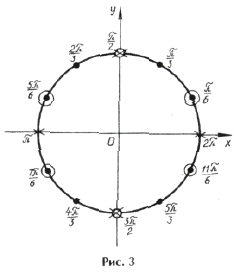
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin 2 x + sin 2 2x = sin 2 3x.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2 p ) = 0.
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
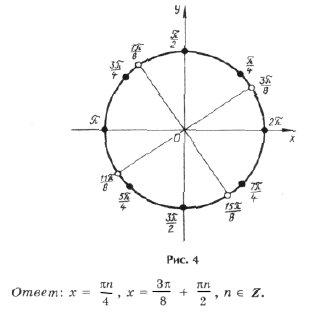
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1( · ) и x3(О), которые не совпадают.
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
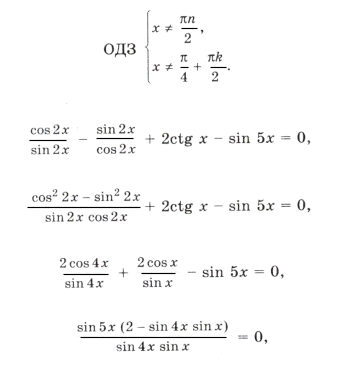
Учитывая ОДЗ, получим
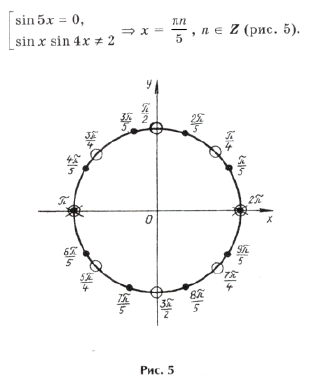
Пример 7.
Иногда случается, что часть серии входит в ответ, а часть нет.
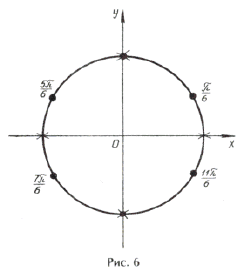
Нанесем на тригонометрический круг (рис. 6) все числа серии 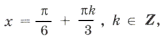
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Пример 8. sin 2 2x + sin 2 3x + sin 2 4x + sin 2 5x = 2.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p ]. Это будут:
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2 p k имеет посторонние корни, удовлетворяющие условию x № 3 p n, n О Z. Пусть p + 2 p k = 3 p n; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2 p k будет при k = 3m + 1, m О Z.
Пример 10. cos 7x (sin 5x – 1) = 0.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Ответ можно записать в виде
Пример 11.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Пример 12.
Решением уравнения является пересечение серий x1 и x2;
где
– целое число;
Пример 13.
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку
,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2 p l, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство
,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2 p ].
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как
то
Пример 16. Найти все решения уравнения
принадлежащие отрезку
.
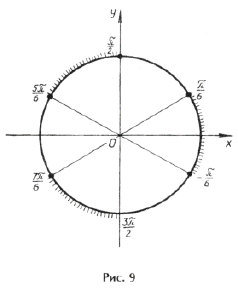
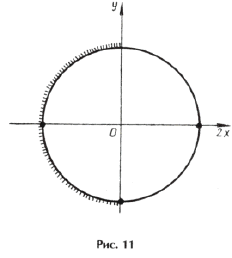
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку
принадлежит только один промежуток из ОДЗ, а именно
.
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos 2 3x Ю sin 2x = cos 6x,
Из серии
при n = 2 имеем
Из серии
при n = 5 имеем
Пример 17.
Ответ:
Пример 18. Найти все корни уравнения
которые удовлетворяют условию
.
10sin 2 x = – cos 2x + 3 Ю 10sin 2 x = 2sin 2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при
.
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут
.
Пример 19.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Ответ:
Пример 21.
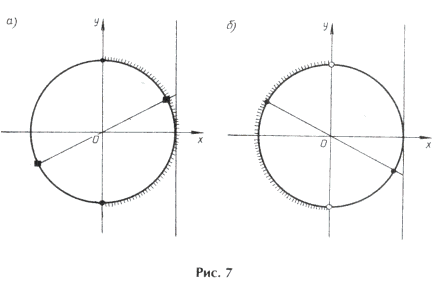
а)
Но ctg x 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:

Л. Максименко,
Р. Зинченко,
г. АнгарскМетоды решения тригонометрических уравнений
Разделы: Математика
Составной частью ЕГЭ являются тригонометрические уравнения.
К сожалению, не существует общего единого метода, следуя которому можно было бы решить любое уравнение, в котором участвуют тригонометрические функции. Успех здесь могут обеспечить лишь хорошие знания формул и умение видеть те или иные полезные комбинации, что вырабатывается лишь практикой.
Общая цель обычно состоит в преобразовании входящего в уравнение тригонометрического выражения к такому виду, чтобы корни находились из так называемых простейших уравнений:
сos px = a; sin gx = b; tg kx = c; ctg tx = d. Для этого необходимо уметь применять тригонометрические формулы. Полезно знать и называть их “именами”:
1. Формулы двойного аргумента, тройного аргумента:
сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;
sin 2x = 2 sin x cos x;
tg 2x = 2 tg x/1 – tg x;
ctg 2x = (ctg 2 x – 1)/2 ctg x;
sin 3x = 3 sin x – 4 sin 3 x;
cos 3x = 4 cos 3 x – 3 cos x;
tg 3x = (2 tg x – tg 3 x)/(1 – 3 tg 2 x);
ctg 3x = (ctg 3 x – 3ctg x)/(3ctg 2 x – 1);
2. Формулы половинного аргумента или понижения степени:
sin 2 x/2 = (1 – cos x)/2; сos 2 x/2 = (1 + cos x)/2;
tg 2 x = (1 – cos x)/(1 + cos x);
ctg 2 x = (1 + cos x)/(1 – cos x);
3. Введение вспомогательного аргумента:
рассмотрим на примере уравнения a sin x + b cos x = c а именно, определяя угол х из условий sin y = b/v(a 2 + b 2 ), cos y = a/v(a 2 + b 2 ), мы можем привести рассматриваемое уравнение к простейшему sin (x + y) = c/v(a 2 + b 2 ) решения которого выписываются без труда; тем самым определяются и решения исходного уравнения.
4. Формулы сложения и вычитания:
sin (a + b) = sin a cos b + cos a sin b;
sin (a – b) = sin a cos b – cos a sin b;
cos (a + b) = cos a cos b – sin a sin b;
cos (a – b) = cos a cos b + sin a sin b;
tg (a + b) = ( tg a + tg b)/(1 – tg a tg b);
tg (a – b) = ( tg a – tg b)/(1 + tg a tg b);
5. Универсальная тригонометрическая подстановка:
cos a = (1 – tg 2 (a/2))/(1 + (tg 2 (a/2));
tg a = 2 tg a/2/(1 – tg 2 (a/2));
6. Некоторые важные соотношения:
cos x + cos 2x + cos 3x +…+ cos mx = (sin (2m+ 1)x/2 – sin (x/2))/(2 sin (x/2));
7. Формулы преобразования суммы тригонометрических функций в произведение:
sin a + sin b = 2 sin(a + b)/2 cos (a – b)/2;
sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;
tg a + tg b = sin (a + b)/(cos a cos b);
tg a – tg b = sin (a – b)/(cos a cos b).
А также формулы приведения.
В процессе решения надо особенно внимательно следить за эквивалентностью уравнений, чтобы не допустить потери корней (например, при сокращении левой и правой частей уравнения на общий множитель), или приобретения лишних корней (например, при возведении обеих частей уравнения в квадрат). Кроме того, необходимо контролировать принадлежат ли получающие корни к ОДЗ рассматриваемого уравнения.
Во всех необходимых случаях (т.е. когда допускались неэквивалентные преобразования), нужно обязательно делать проверку. При решении уравнении необходимо научить учащихся сводить их к определенным видам, обычно начиная с легких уравнении.
Ознакомимся с методами решения уравнений:
1. Сведение к виду аx 2 + bx + c = 0
2. Однородность уравнений.
3. Разложение на множители.
4. Сведение к виду a 2 + b 2 + c 2 = 0
5. Замена переменных.
6. Сведение уравнения к уравнению с одной переменной.
7. Оценка левой и правой части.
8. Метод пристального взгляда.
9. Введение вспомогательного угла.
10. Метод “ Разделяй и властвуй ”.
1. Решить уравнение: sin x + cos 2 х = 1/4.
Решение: Решим методом сведения к квадратному уравнению. Выразим cos 2 х через sin 2 x
4 sin 2 x – 4 sin x – 3 = 0
т.е. х = (-1) к+1 arcsin 1/2 + 
Ответ: (-1) к+1 

2. Решить уравнение: 2 tg x cos x +1 = 2 cos x + tg x,
решим способом разложения на множители
2 tg x cos x – 2 cos x + 1 – tg x = 0,где х
/2 +
k, k€z,
2 cos x (tg x – 1) – (tg x – 1) = 0
(2 cos x – 1) (tg x – 1) = 0
2 cos x – 1 = 0 или tg x – 1 = 0
т.е х = ± 



Ответ: ± 



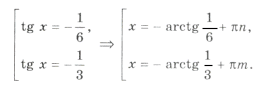
3. Решить уравнение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0.
Решение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0 однородное уравнение 2 степени. Поскольку cos x = 0 не является корнем данного уравнения, разделим левую и правую часть на cos 2 х. В результате приходим к квадратному уравнению относительно tg x
откуда х = 

х = arctg 2 + 
Ответ: 


4. Решить уравнение: cos (10x + 12) + 4
Решение: Метод введения новой переменной
Пусть 5х + 6 = у, тогда cos 2у + 4
1 – 2 sin 2 у + 4
2 sin у – 4 = 0
2t 2 – 4
t = 

sin (5x + 6) = 
5x + 6 = (-1) к 

х = (-1) к 

5. Решить уравнение: (sin х – cos у) 2 + 40х 2 = 0
Решение: Используем а 2 +в 2 +с 2 = 0, верно, если а = 0, в = 0, с = 0. Равенство возможно, если sin х – cos у = 0, и 40х = 0 отсюда:
х = 0, и sin 0 – cos у = 0, следовательно, х = 0, и cos у = 0, отсюда: х = 0, и у = 



Ответ: (0; 

6. Решить уравнение: sin 2 х + cos 4 х – 2 sin х + 1 = 0
Решение: Преобразуем уравнение и применим метод “разделяй и властвуй”
(sin 2 х – 2 sin х +1) + cos 4 х = 0;
(sin х – 1) 2 + cos 4 х = 0; это возможно если
(sin х – 1) 2 = 0, и cos 4 х = 0, отсюда:
sin х – 1 = 0, и cos х = 0,
sin х = 1, и cos х = 0, следовательно
х = 

Ответ: 

7. Решить уравнение: sin 5х + sin х = 2 + cos 2 х.
Решение: применим метод оценки левой и правой части и ограниченность функций cos и sin.
0 

0 + 2 

2 

sin 5х + sin х 

-2 

sin 5х + sin х 
имеем левая часть 

равенство возможно если, они оба равны 2.
cos 2 х = 0, и sin 5х + sin х = 2, следовательно
х = 

Ответ: 

8. Решить уравнение: cos х + cos 2х + cos 3х+ cos 4х = 0.
Решение: Решим методом разложения на множители. Группируем слагаемые, расположенные в левой части, в пары.
(В данном случае любой способ группировки приводит к цели.) Используем формулу cos a+cos b=2 cos (a + b)/2 cos (a – b)/2.
2 cos 3/2х cos х/2 + 2 cos 7/2х cos х/2 = 0,
cos х/2 (cos 3/2х + cos 7/2х) = 0,
2 cos 5/2х cos х/2 cos х = 0,
Ответ: 





Обратим внимание на то, что второй случай включает в себя первый. (Если во втором случае взять к = 4 + 5






Рассмотренное уравнение иллюстрирует весьма типичную схему решения – разложение уравнения на множители за счёт попарной группировки и использования формул:
sin a + sin b = 2 sin (a + b)/2 cos (a – b)/2;
sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведём решения уравнений, иллюстрирующие типичные случаи появления лишних (посторонних) корней и методы “борьбы” с ними.
Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнений. Приведём примеры.
Решение: Приравняем нулю числитель (при этом происходит расширение области определения уравнения – добавляются значения х, обращающие в нуль знаменатель) и постараемся разложить его на множители. Имеем:
2 cos 3х sin х – cos 3х + 2sin х – 1 = 0,
(cos 3х + 1) (2 sin х – 1) = 0.
Получаем два уравнения:
cos 3х + 1 = 0, х =
/3 + 2/3
k.
Посмотрим, какие k нам подходят. Прежде всего, заметим, что левая часть нашего уравнения представляет собой периодическую функцию с периодом 2

Решение этого уравнения основывается на следующем простом соображении: если 0 t убывает с ростом t.
Значит, sin 8 х 

Сложив почленно эти неравенства, будем иметь:
sin 8 х – cos 5 х 
Следовательно, левая часть данного уравнения равна единице тогда и только тогда, когда выполняются два равенства:
sin 8 х = sin 2 х, cos 5 х = cos 2 х,
Ответ: 



Для полноты картины рассмотрим ещё пример.
12. Решить уравнение: 4 cos 2 х – 4 cos 2 3х cos х + cos 2 3х = 0.
Решение: Будем рассматривать левую часть данного уравнения как квадратный трёхчлен относительно cos х.
Пусть D – дискриминант этого трёхчлена:
1/4 D = 4 (cos 4 3х – cos 2 3х).
Из неравенства D 


Значит, возникают две возможности: cos 3х = 0 и cos 3х = ± 1.
Если cos 3х = 0, то из уравнения следует, что и cos х = 0, откуда х = 

Эти значения х удовлетворяют уравнению.
Если 



Ответ: 



13. Решить уравнение: sin 4 x + cos 4 x = 7/2 sin x cos x.
Решение: Преобразуем выражение sin 4 x + cos 4 x,выделив полный квадрат: sin 4 x + cos 4 x = sin 4 x + 2 sin 2 х cos 2 х + cos 4 x – 2 sin 2 х cos 2 х = (sin 2 х + cos 2 х) 2 – 2 sin 2 х cos 2 х, откуда sin 4 x + cos 4 x = 1 – 1/2 sin 2 2х. Пользуясь полученной формулой, запишем уравнение в виде
1-1/2 sin 2 2х = 7/4 sin 2х.
получим квадратное уравнение 2t 2 + 7t – 4 = 0,
решая которое, находим t1 = 1/2, t2 = – 4
уравнение sin 2х = 1/2
уравнение sin 2х = – 4 решений не имеет.
14. Решить уравнение: sin 9х + sin х = 2.
Решение: Решим уравнение методом оценки. Поскольку при всех значениях а выполнено неравенство sin а




Решением будут те значения х, при которых выполнено и первое, и второе уравнение. Поэтому из полученных ответов следует отобрать только х = 

Ответ: 

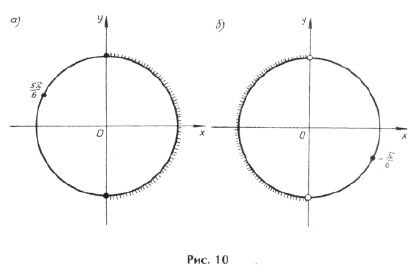
15. Решить уравнение: 2 cos x = 1 – 2 cos 2 x – v3 sin 2х.
Решение: воспользуемся формулой:
сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;
и перепишем уравнение в виде
2 cos x = – cos 2х – 
Применим к правой части процедуру введения дополнительного аргумента. Получим уравнение:
2 cos x = – 2 (1/2 cos 2х + 
которое можно записать в виде
2 cos x = – 2 (cos а cos 2х + sin а sin 2х),
где очевидно, а = 
cos (a – b) = cos a cos b + sin a sin b;
приходим к уравнению
2 cos x = – 2 cos (2х – 
cos x + cos (2х – 
Последнее уравнение легко решить, преобразовав сумму косинусов в произведение по формуле:
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2,
cos x + cos (2х – 


Это уравнение расщепляется на два уравнения
cos (3х/2 –
/6) = 0, и
cos (
решение которых уже не представляет сколь нибудь значительных трудностей.
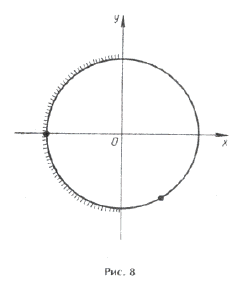
Ответ: 2

16. При каких значениях параметра а, уравнение а sin x – 4 cos x = 5, имеет решения?
Решение: преобразуем левую часть уравнения, используя формулу введения дополнительного аргумента:
а sin x – 4 cos x = 


Но значение y нас не интересует. Поэтому данное уравнение перепишем в виде

sin (x – y) = 5/




Решим это неравенство:
5/
(а 2 + 16)
1, обе части умножим на
(а 2 + 16):
5 


а 2 + 16 
а 2 



а € (-

Ответ: (-

17. При каких значениях параметра а, уравнение 2 sin 2 x + 3 cos (x +2 а) = 5, имеет решения?
Это означает, что исходное уравнение равносильно системе уравнений sin 2 x = 1, и cos (x +2 а) = 1.
sin x = – 1, sin x = 1, cos (x +2 а) = 1;
х = 


х = 





2 а = 2 


а = 


а = – 

а = – 

Ответ: – 

Рассмотренные выше примеры лишь иллюстрируют несколько общих рекомендаций, которые полезно учитывать при решении тригонометрических уравнений. Из приведённых примеров видно, что дать общий рецепт в каждом конкретном случае невозможно.
Ежегодно варианты экзаменационных материалов ЕГЭ содержат от 4-х до 6-ти различных задач по тригонометрии. Поэтому параллельно с повторением теоретического материала значительное время должно быть отведено решению конкретных задач, в том числе и тригонометрических уравнений. А умение можно выработать, только получив практические навыки в решении достаточного числа тригонометрических уравнений.
 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях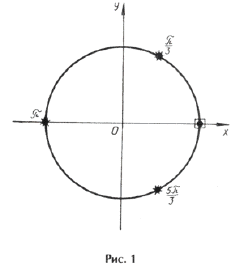
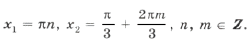
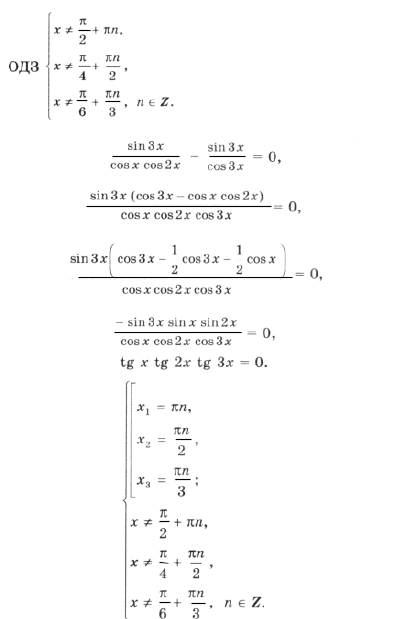
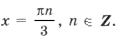
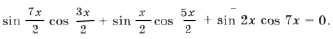
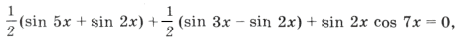
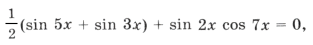
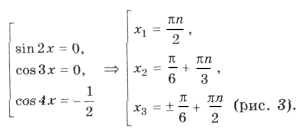
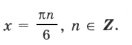
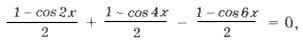
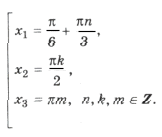
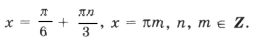
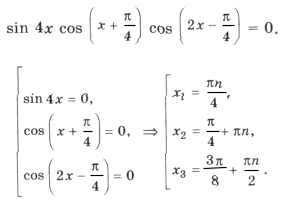
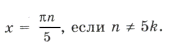
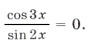
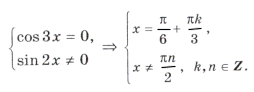
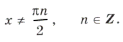
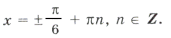
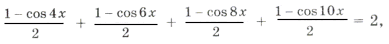
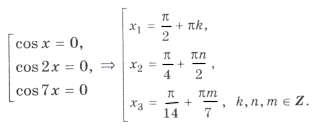
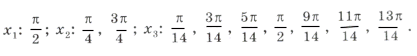
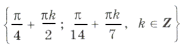
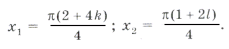
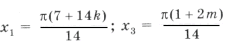
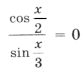
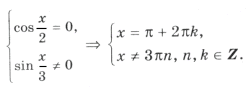
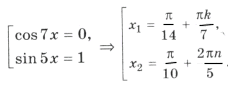
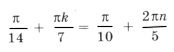
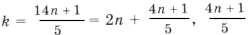 – целое число.
– целое число.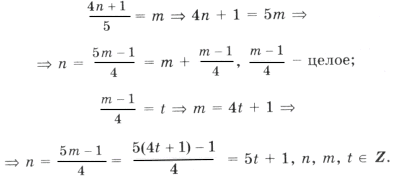
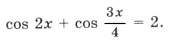
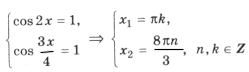
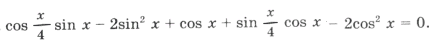
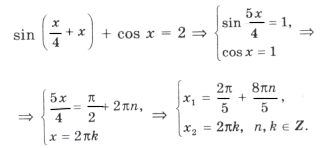
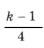 – целое число;
– целое число;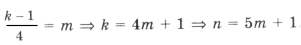
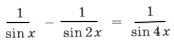
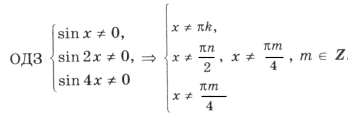
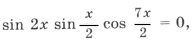
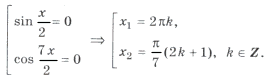
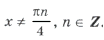
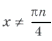 ,
,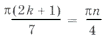 ,
,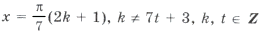
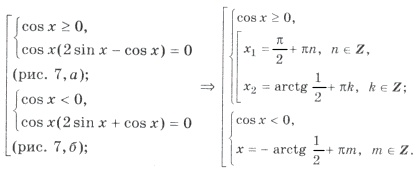

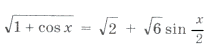
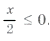
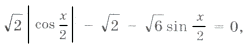
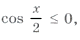 то
то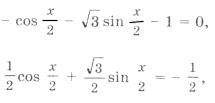
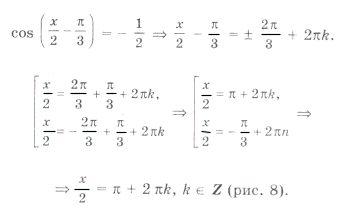
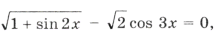
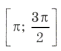 .
.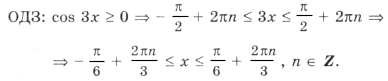
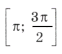 принадлежит только один промежуток из ОДЗ, а именно
принадлежит только один промежуток из ОДЗ, а именно 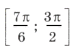 .
.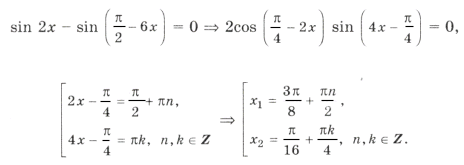
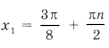 при n = 2 имеем
при n = 2 имеем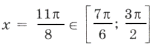
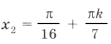 при n = 5 имеем
при n = 5 имеем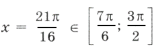
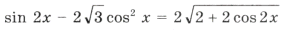
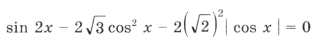
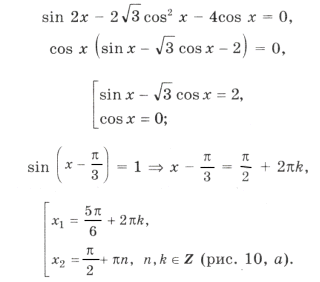
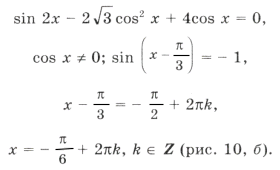
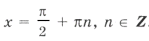
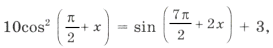
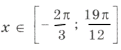 .
.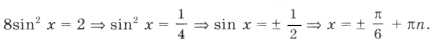
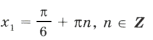
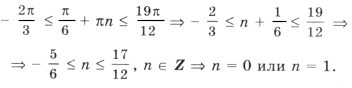
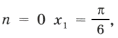
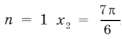 .
.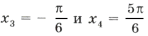 .
.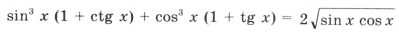
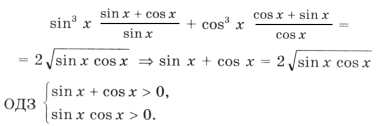
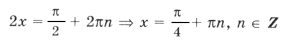
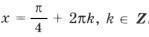
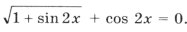
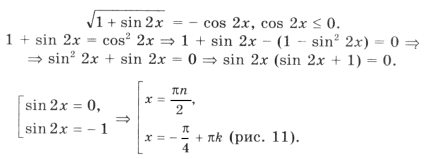
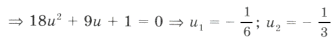
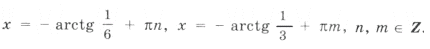
 .
.