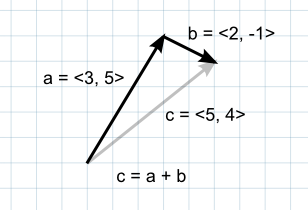Что такое vector в unity
Математика в Gamedev по-простому. Векторы и интегралы
Всем привет! Сегодня хотелось бы поговорить о математике. Математика очень интересная наука и она может сильно пригодиться при разработке игр, да и в целом при работе с компьютерной графикой. Многие (особенно новички) просто не знают о том, как она применяется при разработке. Существует множество задач, не требующих глубокого понимания таких понятий как: интегралы, комплексные числа, группы, кольца и др, но благодаря математике вы можете решать многие интересные задачи. В этой статье мы рассмотрим векторы и интегралы. Если интересно, добро пожаловать под кат. Иллюстрирующий Unity проект, как всегда, прилагается.
Векторная математика.
Векторы и векторная математика являются необходимыми инструментами для разработки игр. Многие операции и действия завязаны на ней целиком. Забавно, что для реализации класса, который отображает стрелочку вектора в Unity, уже потребовалось большинство типовых операций. Если вы хорошо разбираетесь в векторной математике данный блок вам будет неинтересен.
Векторная арифметика и полезные функции
Аналитические формулы и прочие детали легко нагуглить, так что не будем тратить на это время. Сами операции будут проиллюстрированы гиф-анимациями ниже.
Важно понимать, что любая точка в сущности является вектором с началом в нулевой точке.
Гифки делались с помощью Unity, так что нужно было бы реализовывать класс, отвечающий за отрисовку стрелочек. Стрелка вектора состоит из трех основных компонент – линии, наконечника и текста с именем вектора. Для отрисовки линии и наконечника я воспользовался LineRenderer. Посмотрим на класс самого вектора:
Так как мы хотим, чтобы вектор был определённой длинны и точно соответствовал точкам, которые мы задаём, то длинна линии рассчитывается по формуле:
В данной формуле (_VectorEnd — _VectorStart).normalized – это направление вектора. Это можно понять из анимации с разницей векторов, приняв что _VectorEnd и _VectorStart – это вектора с началом в (0,0,0).
Дальше разберём две оставшиеся базовые операции:
Нахождение нормали (перпендикуляра) и середины вектора – это очень часто встречающиеся задачи при разработке игр. Разберём их на примере размещения подписи над вектором.
Для того, чтобы разместить текст перпендикулярно вектору нам понадобится нормаль. В 2D графике нормаль находится достаточно просто.
Вот мы и получили нормаль к отрезку.
Дальше остаётся поместить его в середину вектора и поднять по нормали на расстояние, которое будет смотреться красиво.
В коде использованы локальные позиции, чтобы можно была возможность двигать получившуюся стрелочку.
Но это было про 2D, а что же с 3D?
В 3D плюс-минус всё тоже самое. Отличается только формула нормали, так как нормаль уже берётся не к отрезку, а к плоскости.
В данном примере контролла нормаль к плоскости используется, чтобы сместить конечную точку траектории право, чтобы планету не загораживал интерфейс. Нормаль в 3д графике – это нормализованное векторное произведение двух векторов. Что удобно, в Юнити есть обе эти операции и мы получаем красивую компактную запись:
Думаю, многим, кто думает, что математика не нужна и зачем вообще это знать, стало чуть понятнее какие задачи с помощью неё можно решать просто и элегантно. Но это был простой вариант, который должен знать каждый разработчик игр не стажёр. Поднимем планку — поговорим об интегралах.
Вообще у интегралов очень много применений, таких как: физические симуляции, VFX, аналитика и многое другое. Я не готов сейчас детально описывать все. Хочется описать простой и визуально понятный. Поговорим про физику.
Допустим есть задача – двигать объект в определённую точку. К примеру, чтобы при вхождении в определённый триггер, должны вылетать книги с полок. Если вы хотите двигать равномерно и без физики, то задача тривиальна и не требует интегралов, но когда книги выталкивает с полки призрак, такое распределение скорости будет смотреться совсем не так.
Что такое интеграл?
По сути это площадь под кривой. Но что это означает в контексте физики? Допустим у вас есть распределение скорости по времени. В данном случае площадь под кривой – это путь который пройдёт объект, а это как раз то, что нам и нужно.
Если перейти от теории к практике, то в Unity есть замечательный инструмент под названием AnimationCurve. С помощью него можно задать распределение скорости с течением времени. Создадим вот такой класс.
Метод GetApproxSquareAnimCurve – это и есть наше интегрирование. Мы делаем его простейшим численным методом, просто идём по значениям фукнции и суммируем их определённое число раз. Я выставил 1000 для верности, в целом можно подобрать оптимальнее.
Благодаря этой площади мы дальше уже знаем, какое относительное расстояние. А дальше сравнив два пройденных пути мы получаем коэффициент скорости speedK, который отвечает за то, чтобы мы прошли заданное расстояние.
Как работают векторы. Баскетбол на Unity 3D
Учебные материалы для школы программирования. Часть 16
В этой статье, мы обратим свой взор в прошлое, и вспомним, с чего начиналась детская школа программирования Step to Science. Первоначальная идея проекта состояла в том, чтобы быть не просто кружком технического творчества, а стать для детей ответом на вопрос, «зачем учиться в школе?»
К чему нам физика, алгебра и геометрия, если мы не планируем проектировать космические корабли, если для счета у нас есть калькулятор в телефоне, расплачиваемся мы чаще картой, так что даже сдачу в уме считать не надо.
Я тоже в детстве вела такие рассуждения, и у родителей не было иных способов донести до меня истину, кроме фразы «нет слова не хочу, есть слово надо» и ремня, который без лишней полемики мотивировал садиться за уроки.
Порядок выполнения
На примере создания 2D игры «баскетбол», рассмотрим векторы (скорости, сил, локальной и глобальной систем координат). Разберем принципы представления систем координат и представления векторов. Также будет затронута работа с LineRenderer и многокамерность.
Создадим новый проект и импортируем в него приложенный ассет.
Ассет содержит в себе все ресурсы, необходимые для создания полноценного 2D приложения.
Для начала создадим небольшую сцену, в качестве фона выберем спрайт «спортзал» и установим на него сетку. Обратите внимание, что необходимо выставить коллайдеры для щита и корзины.
Конечно, необходимо выставить правильный Order in layer у спрайтов. Добавим мяч, применим к нему Circle collider и Rigidbody.

Внутри мяча должен находиться пустой объект с Audio Source, настроенным на воспроизведение звука удара.

Чтобы воспроизводить этот звук, напишем простой скрипт, закинем его на мяч и сконфигурируем.
В скрипте нет автопоиска Rigidbody, так что придётся закинуть его руками. Если нажать на Play, наш мяч упадёт, издавая звуки. Чтобы мяч отскакивал, создадим физический материал и закинем его на коллайдер мяча.
Теперь подумаем о том, чтобы мяч показывал своё направление. Для этого создадим скрипт, который рисует стрелки: нам понадобятся два пустых объекта с LineRenderer, один в другом.
Создадим материал для стрелки:
И добавим скрипт, который будет выставлять вершины LineRenderer’ов, делая из них стрелки:
Закинем скрипт на объект-родитель стрелки и настроим его.

Теперь надо написать скрипт, который будет вектор скорости передавать в наш скрипт «показывания» стрелки. Он очень простой:
Закинем его на мяч, в скрипте укажем риджибади мяча и объект со скриптом стрелки.
Теперь сделаем так, чтобы мяч можно было кидать. Для этого необходимо выставить ему тип Rigidbody как Kinematic и написать небольшой скрипт.

Скрипт выкладываем на пустой объект в мире и устанавливаем ему наш мяч в качестве риджитбади и его трейл.

Внутри панели должен лежать спрайт со следующими параметрами (обратите внимание на привязку):

Для того, чтобы при компиляции не возникало ошибок из-за отсутствия класса спавнера, данный скрипт приложен отдельным ассетом, и импортировать его можно только после создания спавнера.
Для того, чтобы сделать включение/выключение стрелок, используется скрипт Toggle, который реализован через эвент-систему юнити. Его необходимо закинуть на кнопку и сконфигурировать следующим образом.
Vectors are a fundamental mathematical concept which allow you to describe a direction and magnitude. In games and apps, vectors are often used to describe some of the fundamental properties such as the position of a character, the speed something is moving, or the distance between two objects.
Vector arithmetic is fundamental to many aspects of computer programming such as graphics, physics and animation, and it is useful to understand it in depth to get the most out of Unity.
Vectors can be expressed in multiple dimensions, and Unity provides the Vector2, Vector3 and Vector4 classes for working with 2D, 3D, and 4D vectors. These three types of Vector classes all share many of the same functions, such as magnitude, so most of the information on this page applies to all three types of Vector unless otherwise specified.
This page provides an overview of the Vector classes and their common uses when scripting with them. For an exhaustive reference of every member of the vector classes, see the script reference pages for Vector2, Vector3 and Vector4.
Understanding Vector Arithmetic
Addition
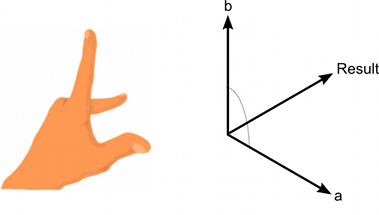
When two vectors are added together, the result is equivalent to taking the original vectors as “steps”, one after the other. Note that the order of the two parameters doesn’t matter, since the result is the same either way.
If the first vector is taken as a point in space then the second can be interpreted as an offset or “jump” from that position. For example, to find a point 5 units above a location on the ground, you could use the following calculation:-
If the vectors represent forces then it is more intuitive to think of them in terms of their direction and magnitude (the magnitude indicates the size of the force). Adding two force vectors results in a new vector equivalent to the combination of the forces. This concept is often useful when applying forces with several separate components acting at once (eg, a rocket being propelled forward may also be affected by a crosswind).
Although the examples here show 2D vectors, the same concept applies to 3D and 4D vectors.
Subtraction
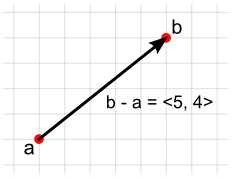
Vector subtraction is most often used to get the direction and distance from one object to another. Note that the order of the two parameters does matter with subtraction:-
As with numbers, adding the negative of a vector is the same as subtracting the positive.
The negative of a vector has the same magnitude as the original and points along the same line but in the exact opposite direction.
Direction and Distance from One Object to Another
If one point in space is subtracted from another, then the result is a vector that “points” from one object to the other:
As well as pointing in the direction of the target object, this vector’s magnitude is equal to the distance between the two positions. You may need a “normalized” vector giving the direction to the target, but with a fixed distance (say for directing a projectile). You can normalize a vector by dividing it by its own magnitude:
This approach is preferable to using both the magnitude and normalized properties separately, since they are both quite CPU-hungry (they both involve calculating a square root).
If you only need to use the distance for comparison (for a proximity check, say) then you can avoid the magnitude calculation altogether. The sqrMagnitude property gives the square of the magnitude value, and is calculated like the magnitude but without the time-consuming square root operation. Rather than compare the magnitude against a known distance, you can compare the squared magnitude against the squared distance:-
This is much more efficient than using the true magnitude in the comparison.
Sometimes, when working in 3D, you might need an “overground heading” to a target. For example, imagine a player standing on the ground who needs to approach a target floating in the air. If you subtract the player’s position from the target’s then the resulting vector will point upwards towards the target. This is not suitable for orienting the player’s transform since they will also point upwards; what is really needed is a vector from the player’s position to the position on the ground directly below the target. You can obtain this by taking the result of the subtraction and setting the Y coordinate to zero:-
Scalar Multiplication and Division
When discussing vectors, it is common to refer to an ordinary number (eg, a float value) as a scalar. The meaning of this is that a scalar only has “scale” or magnitude whereas a vector has both magnitude and direction.
Multiplying a vector by a scalar results in a vector that points in the same direction as the original. However, the new vector’s magnitude is equal to the original magnitude multiplied by the scalar value.
Likewise, scalar division divides the original vector’s magnitude by the scalar.
These operations are useful when the vector represents a movement offset or a force. They allow you to change the magnitude of the vector without affecting its direction.
When any vector is divided by its own magnitude, the result is a vector with a magnitude of 1, which is known as a normalized vector. If a normalized vector is multiplied by a scalar then the magnitude of the result will be equal to that scalar value. This is useful when the direction of a force is constant but the strength is controllable (eg, the force from a car’s wheel always pushes forwards but the power is controlled by the driver).
Dot Product
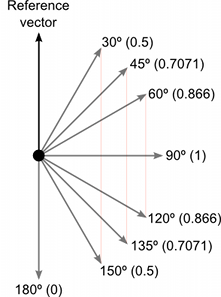
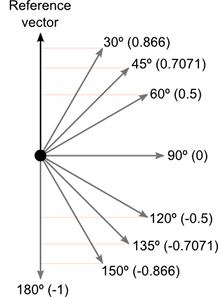
Below you can see a comparison of how vectors of varying angles compared with a reference vector return a dot product value between 1 and –1 :
The dot product is a mathematically simpler operation than calculating the cosine, so it can be used in place of the Mathf.Cos function or the vector magnitude operation in some circumstances (it doesn’t do exactly the same thing but sometimes the effect is equivalent). However, calculating the dot product function takes much less CPU time and so it can be a valuable optimization.
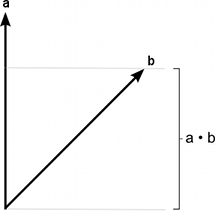
The dot product is useful if you want to calculate the amount of one vector’s magnitude that lies in the direction of another vector.
Naturally, the direction can be anything you like but the direction vector must always be normalized for this calculation. Not only is the result more correct than the magnitude of the velocity, it also avoids the slow square root operation involved in finding the magnitude.
Cross Product
The cross product is only meaningful for 3D vectors. It takes two 3D vectors as input and returns another 3D vector as its result.
The result vector is perpendicular to the two input vectors. You can use the “right hand screw rule” to remember the direction of the output vector from the ordering of the input vectors. If you can curl your fingers in the order of the input vectors, your thumb points in the direction of the output vector. If the order of the parameters is reversed then the resulting vector will point in the exact opposite direction but will have the same magnitude.
The magnitude of the result is equal to the magnitudes of the input vectors multiplied together and then that value multiplied by the sine of the angle between them. Some useful values of the sine function are shown below:-
The cross product can seem complicated since it combines several useful pieces of information in its return value. However, like the dot product, it is very efficient mathematically and can be used to optimize code that would otherwise depend on slower transcendental functions such as sine and cosine.
Computing a Normal/Perpendicular vector

The “left hand rule” can be used to decide the order in which the two vectors should be passed to the cross product function. As you look down at the top side of the surface (from which the normal will point outwards) the first vector should sweep around clockwise to the second:
The result will point in exactly the opposite direction if the order of the input vectors is reversed.
For meshes, the normal vector must also be normalized. This can be done with the normalized property, but there is another trick which is occasionally useful. You can also normalize the perpendicular vector by dividing it by its magnitude:-
Another useful note is that the area of the triangle is equal to perpLength / 2. This is useful if you need to find the surface area of the whole mesh or want to choose triangles randomly with probability based on their relative areas.
Понимание векторной арифметики
Сложение
При сложении 2 векторов результат эквивалентен тому, что получится если исходные векторы принять за следующие друг за другом “шаги”. Заметьте, что порядок двух слагаемых не важен, т.к. в любом случае результат будет одинаковый.
Если первый вектор принять за точку в пространстве, то второй вектор можно интерпретировать как сдвиг или “прыжок” из этой точки. Например, чтобы для поиска точки 5-тью единицами выше точки на земле, вы могли бы использовать следующий расчёт:-
Вычитание
Вычитание векторов чаще всего используется, чтобы узнать расстояние и направление одного объекта относительно другого. Заметьте, что при вычитании порядок параметров имеет значение:-
Отрицательный вектор имеет ту же величину, что и исходный вектор, и лежит на той же прямой, только в обратном направлении.
Скалярные умножение и деление
Говоря о векторах, в порядке вещей обращаться к обычным числам (например, значениям типа float) как к скалярам. Это значит, что у них есть только “размер” или величина, в то время как у векторов есть и величина и направление.
Умножение вектора на скаляр даёт в результате вектор, с тем же направлением, что и исходный вектор. Тем не менее, величина нового вектора равна исходной величине умноженной на скалярное значение.
Аналогично, скалярное деление делит исходную величину вектора на скаляр.
Эти операции полезны, когда вектор представляет из себя смещение движения или силу. Они позволяют вам изменить величину вектора без влияния на его направление.
Скалярное произведение (Dot Product)
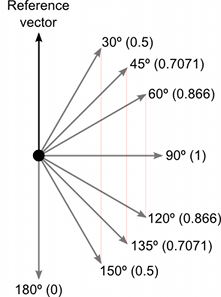
Если работать с точки зрения углов, то можно достаточно просто найти соответствующие косинусы используя калькулятор. Тем не менее, полезно иметь интуитивное понимание основных значений косинуса, как показано на диаграмме ниже:-
Векторное произведение (Cross Product)
Другие операции предназначены для 2D или 3D векторов и для действительных векторов с любым числом измерений. Векторное произведение же, напротив, имеет смысл применять только для 3D векторов. Оно использует 2 вектора как входную информацию и возвращает ещё один вектор в качестве результата.
Итоговый вектор перпендикулярен двум исходным векторам. Можно использовать “правило левой руки”, чтобы запомнить направление выходного вектора относительно исходных векторов. Если первый параметр совпадает с большим пальцем руки, а второй параметр с указательным пальцем, то результат будет указывать в направлении среднего пальца. Если использовать обратный порядок параметров, то тогда итоговый вектор будет указывать в противоположном направлении, но его величина не изменится.
Величина результата равна произведению величин исходных векторов, умноженному на синус угла между ними. Некоторые полезные значения функции синуса указаны ниже:-
Векторное произведение может выглядеть сложным, т.к. оно включает в себя сразу несколько полезных частей информации в возвращённой величине. Тем не менее, как и скалярное произведение, оно очень эффективно с математической точки зрения и может быть использовано для оптимизации кода, который иначе будет зависеть от медленных и сложных функций. Если векторы представляют собой силы, то более естественно будет думать о них с точки зрения их направления и величины (величина определяет мощность силы). Сложение двух векторов силы в результате даёт новый вектор, эквивалентный комбинации этих сил. Этот концепт зачастую очень полезен при применении сил с различными раздельными компонентами, которые работают одновременно (например, на летящую вперёд ракету может влиять встречный или боковой ветер).
Unity vs Vector. Как и почему стоит использовать вектор в мобайле?
Отличная новость — Unity теперь поддерживает SVG
Добавить и ознакомится с ним можно запустив Unity, а далее:
Window — Package Manager — All Packages — Vector Graphics
Какие есть плюсы и минусы
В общем
Работает “вектор” через Sprite Renderer, но он не идентичен стандартному Sprite Renderer. В нём нету возможности ни окраски, ни прозрачности(не можно изменять прозрачность).
Как вы понимаете, раз он является плодом MeshRenderer, то соответственно нету еще двух ключевых особенностей: Tiling и Slicing. Кроме этого, как Image его тоже не можно использовать.
Для иконок подойдет
Это идеальное решение для всяческих иконок.
Естественно для одноцветных и более-менее простых (какими и должны они быть).
Производительность
При 2160 * 1080 и “625 снепе” 200 тысяч вершин: 53 — 55 фпс
При 2560 * 1440 и “820 снепе” 200 тысяч вершин: 58 — 60 фпс
При таком количестве вершин — отличный результат, наверное остается вопрос сколько drawcalls было? — Ровно 37.
Как обстоят дела с отрисовкой
Как известно меши до 900 вершин объединяются by batching в один drawcall, при условии что материал одинаковый. Именно так и происходит с SVG файлами, они тоже имеют данное свойство, обратная сторона медали — отсутствие добавления “спрайтов” в атлас, хоть это и абсурдно.
Что даст замена растра на вектор
Выводы
Можно ли заменить UI — нет.
Можно ли заменить игровых персонажей, локации … — неоднозначное да.