Что такое exp в паскале
exp в паскале что это
Функция Exp в Паскале (и многих других языках программирования) вычисляет экспоненту. Синтаксис:
function Exp(X : ValReal) : ValReal;
О типе ValReal я рассказывал здесь.
Функция Exp X вычисляет и возвращает экспоненту числа X.
Вычисление экспоненты — это вычисление числа е в степени X. То есть
Подробности см. в видео и читайте в статье далее.
Обратная функция Ln
Если вы помните функцию Ln, то вы также помните, что она вычисляет натуральный логарифм.
Так вот, обратной функцией Exp является функция Ln. Иными словами, обратная функция экспоненциальной функции (экспоненты) — это натуральный логарифм. То есть:
e X = Exp(X) = Exp(Ln(Y)) = Y
Есть ещё вот такая полезная формула:
x Y = e Y ln(x) = Exp(Y * Ln(X))
Из этого следует, что используя функции Ln и Exp, мы можем возвести любое число в любую степень. Сделать это можно, например, так:
Если описать это математическим языком, то приведённое выше выражение будет эквивалентно следующей записи:
Правда, надо сказать, что здесь есть нюансы. Есть частные случаи, когда приведённое выше выражение выдаст неправильный результат. Например, когда Y или X отрицательные числа, или когда они равны нулю. Такие ситуации надо обрабатывать дополнительно. Однако эта статья не о возведении в степень, поэтому мы будем рассматривать эти частные случаи в другой статье.
Пример исходного кода, где используется функция Exp:
Функция Exp Pascal-Паскаль
Описание
Exp: функция — Возвращает экспоненту параметра.
| Объявление: | Function Exp(X: Real): Real; |
|---|---|
| Режим: | Windows, Real, Protected |
Замечания:
Возвращаемое значение:
Значение e возведенное в степень X, где e — основание натуральных логарифмов.
Пример программы для функции Exp
Программирование
Исходники Pascal (127)
Справочник
Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту
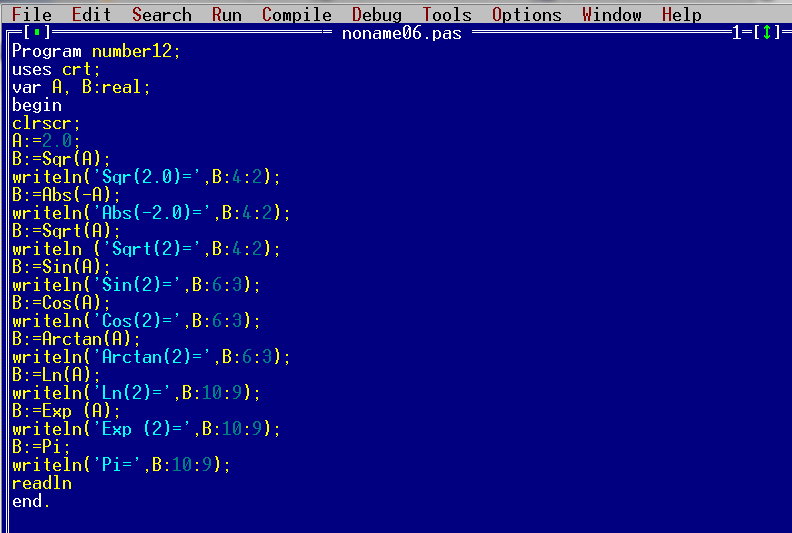
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.
В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.
В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».
В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.
Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.
Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.
Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.
Строка №21. Функция Exp возводит число «e» (экспонента — 2.72. ) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».
Строка №23. Переменной «B» будет присвоено значение числа «?».
Дополнение к материалу.
Exp в информатике это
Функция Exp в Паскале (и многих других языках программирования) вычисляет экспоненту. Синтаксис:
function Exp(X : ValReal) : ValReal;
О типе ValReal я рассказывал здесь.
Функция Exp X вычисляет и возвращает экспоненту числа X.
Вычисление экспоненты – это вычисление числа е в степени X. То есть
Подробности см. в видео и читайте в статье далее.
Обратная функция Ln
Если вы помните функцию Ln, то вы также помните, что она вычисляет натуральный логарифм.
Так вот, обратной функцией Exp является функция Ln. Иными словами, обратная функция экспоненциальной функции (экспоненты) – это натуральный логарифм. То есть:
e X = Exp(X) = Exp(Ln(Y)) = Y
Есть ещё вот такая полезная формула:
x Y = e Y ln(x) = Exp(Y * Ln(X))
Из этого следует, что используя функции Ln и Exp, мы можем возвести любое число в любую степень. Сделать это можно, например, так:
Если описать это математическим языком, то приведённое выше выражение будет эквивалентно следующей записи:
Правда, надо сказать, что здесь есть нюансы. Есть частные случаи, когда приведённое выше выражение выдаст неправильный результат. Например, когда Y или X отрицательные числа, или когда они равны нулю. Такие ситуации надо обрабатывать дополнительно. Однако эта статья не о возведении в степень, поэтому мы будем рассматривать эти частные случаи в другой статье.
Пример исходного кода, где используется функция Exp:
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr – квадрат числа, Abs – модуль числа, Sqrt – корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.
В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.
В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».
В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.
Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.
Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.
Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.
Строка №21. Функция Exp возводит число «e» (экспонента – 2.72. ) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».
Строка №23. Переменной «B» будет присвоено значение числа «?».
Дополнение к материалу.
В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.
Описание
Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.
Синтаксис
Аргументы функции EXP описаны ниже.
Число — обязательный аргумент. Показатель степени, в которую возводится основание e.
Замечания
Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).
Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Приблизительное значение e
Основание натурального логарифма e, возведенное в квадрат
Pascal-Паскаль
Программирование. Стандартные функции Pascal-Паскаль
Программирование. Стандартные функции Pascal-Паскаль
Стандартные функции Pascal-Паскаль
| Стандартные математические функции Турбо Паскаля | |||
|---|---|---|---|
| Обращение | Тип аргумента | Тип результата | Примечание |
| Abs(x) | Real, integer | Тип аргумента | Модуль аргумента |
| ArcTan(x) | Real, integer | Real | Арктангенс (значение в радианах) |
| Cos(x) | Real, integer | Real | Косинус, угол в радианах |
| Exp(x) | Real, integer | Real | Экспонента |
| Frac(x) | Real | Real | Дробная часть числа |
| Int(x) | Real, integer | Real | Целая часть числа |
| Ln(x) | Real, integer | Real | Логарифм натуральный |
| Pi | Нет | Real | 3,141592653 |
| Sin(x) | Real, integer | Real | Синус, угол в радианах |
| Sqr(x) | Real, integer | Тип аргумента | Квадрат аргумента |
| Sqrt(x) | Real, integer | Real | Корень квадратный |
| Random | Нет | Real | Псевдослучайное число в интервале [0, 1] |
| Random(I) | Integer | Integer | Псевдослучайное число в интервале [0, I] |
| Round(x) | Real | Integer | Округление до ближайшего целого |
| Trunc(x) | Real | Integer | Отбрасывание дробной части числа |
Порядок вычислений в выражениях следующий:
Хотя нет ограничений на сложность выражений, однако выражения, содержащие более 7 операндов, трудны для чтения и понимания и поэтому такие выражения не рекомендуется использовать.
Выражение на Паскале: exp(3*ln(x)/2)-7*x+sin(x+2)/cos(x+2)
Операторы действия
Пример оператора присваивания
Оператор присваивания, несмотря на кажущуюся простоту, имеет очень важное алгоритмическое значение.
Удобно считать, что выполнение присваивания переменной некоторого значения означает помещение этого значения в выделенный для переменной ящик. При этом каждый запоминающий ящик обладает следующими свойствами.
Ввод и вывод данных
Пример ввода данных с клавиатуры
read(a,b,c);
readln(a,b,c);
Вывод данных на экран производится с помощью стандартной процедуры write( ) или ее разновидности writeln( ).
Список вывода может содержать константы, переменные, выражения, формат вывода. Выражения в списке вывода разделяются запятыми.
Пример вывода данных на экран
write(a,b,c);
writeln(a,b,c);
Окончание ln в имени процедуры означает, что курсор автоматически будет переведен в начало следующей строки экрана.
Программирование
Исходники Pascal (127)
Справочник
Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту
Стандартные функции языка Pascal
В программировании, как и в любой науке (хотя это и искусство также), с течением исторического времени накапливается опыт, методы решения различных задач. Решение многих задач является достаточно универсальным. Незачем каждый раз писать алгоритм для ее решения, если он уже был написан много лет назад и одобрен сообществом программистов. Такие алгоритмы оформляются в виде функций и модулей, а затем используются в программах, которые пишутся здесь и сейчас.
Функция или процедура может быть уже включена в сам язык программирования, а может входить в модуль, который требуется «подключить» к программе.
Ниже описаны стандартные (включенные в язык) функции языка программирования Паскаль.
Арифметические функции
Арифметические функции можно использовать только с величинами целого и вещественного типа.
| Функция | Назначение | Тип результата |
| abs (x) | абсолютное значение аргумента | совпадает с типом аргумента |
| sqr (x) | квадрат аргумента | совпадает с типом аргумента |
| sqrt (x) | квадратный корень аргумента | вещественный |
| cos (x) | косинус аргумента | вещественный |
| sin (x) | синус аргумента | вещественный |
| arctan (x) | арктангенс аргумента | вещественный |
| exp (x) | e x | вещественный |
| ln (x) | натуральный логарифм | вещественный |
| int (x) | целая часть числа | вещественный |
| frac (x) | дробная часть числа | вещественный |
Функции преобразования типов
Эти функции предназначены для преобразования типов величин, например, символа в целое число, вещественного числа в целое и т.д.
Pascal. Стандартные функции и выражения
Стандартные функции.
В программировании, довольно часто приходиться выполнять однотипные действия, причем в задачах разного уровня и класса. И для ускорения процесса написания кода эти действия выносят в специальные подпрограммы – стандартные функции. Обращение к такой подпрограмме происходит по ее имени, а в скобках указывается значение аргумента. В следующей таблице указаны те стандартные функции, которые используются в языке программирования Pascal.
| Функция | Назначение |
| ABS(x) | Вычисление абсолютного значения x: |х| |
| SQR(x) | Вычисление квадрата x: x*x |
| SIN(x) | Вычисление синуса x: sin x |
| COS(x) | Вычисление косинуса x: cos x |
| ARCTAN(x) | Вычисление арктангенса x: arctg x |
| EXP(x) | Вычисление экспоненты (числа Е) в степени x |
| EXP10(x) | Вычисление 10 в степени x |
| LN(x) | Вычисление натурального логарифма x |
| LOG(x) | Вычисление десятичного логарифма x |
| SQRT(x) | Вычисление квадратного корня из x |
| A DIV B | Вычисление частного при делении А на В с отбрасыванием остатка |
| A MOD B | Нахождение остатка от делении А на В |
| TRUNC(x) | Нахождение целой части x |
| RANDOM(x) | Псевдослучайное число в интервале [0, x] |
| ROUND(x) | Округление значения x в сторону ближайшего целого |
| ODD(x) | Проверяет аргумент на нечетность. Результат TRUE, если аргумент нечетный, FALSE – если четный. |
| ORD(x) | Возвращает порядковый номер аргумента и, как следствие, преобразует величину порядкового типа в величину целого типа. |
| CHR(x) | Определение символа языка Паскаль по его порядковому номеру |
| SUCC(x) | Нахождение элемента, идущего после данного в перечне допустимых элементов |
| PRED(x) | Нахождение элемента, идущего перед данным в перечне допустимых элементов |
| FRAC(X) | Возвращает дробную часть x |
| INT(X) | Возвращает целую часть x |
| Pi | Значение математической постоянной π |
| EOF(x) | Возвращает TRUE, если файл находится в стоянии “конец файла”, иначе FALSE, если нет конца файла |
Выражения
Выражение состоит из переменных, констант, полей в записях, указателей функций, круглых скобок и знаков операций. Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров.
1) 12+3*3=21 (12+3)*3=45
2) ( a >1) and ( a 3) (a+3>0) and (a+3 1) and (b
Логическая операция OR (или) суть дизъюнкция в логики и поэтому имеет следующую таблицу истинности:
Ложь имеет место только когда X и Y ложны (нули). В том случае, чтобы истина возвращалась только тогда, когда одно из условий верно следует применить оператор XOR (исключающее или):
(a+3>0) and (a+3 1) and (b
4) x ^( a ) = exp( a *ln( x ))
В Pascal нет функции возведения числа в степень (кроме степени 2), поэтому существует два пути:
1 — умножать число само на себя, какое то количество раз;
2 — воспользоваться функциями экспоненты и натурального логарифма.
В этом примере использованы оба варианта, но если степень, в которую необходимо возвести число, достаточно велика, то предпочтение следует отдать второму способу.