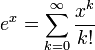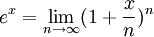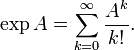Что такое exp в физике
Что такое Экспонента
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
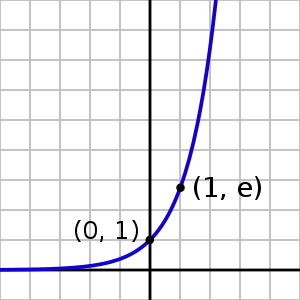
График экспоненты выглядит следующим образом:
Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
И эти вычисления дали нам следующий результат:
Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):
Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Экспоненциальная функция
Содержание
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:
Свойства
Экспонента от комплексного аргумента
От комплексного аргумента z = x + iy экспонента определяется следующим образом:
Вариации и обобщения
Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: 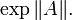
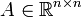
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 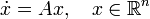
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :
См. также
Полезное
Смотреть что такое «Экспоненциальная функция» в других словарях:
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь
экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика
экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь
экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas
Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь
экспоненциальная — функция [ Словарь иностранных слов русского языка
Мировые константы «пи» и «e» в основных законах физики и физиологии
Доктор геолого-минералогических наук, кандидат физико-математических наук Б. ГОРОБЕЦ.
(напоминаем, что факториал n! =1 x 2 x 3 x … x n);
(последним дан ряд Ньютона, есть и другие ряды).
Все это так, но, как известно, числа 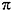
Число 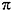
Сначала сформулируем первый основной тезис, а затем поясним его смысл и следствия.
1. Число 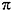
Отсюда вытекают общеизвестные следствия, которые изучают в средней школе.
Разберем еще одну нетривиальную ситуацию, встречающуюся в теории вероятностей. Она касается важной формулы вероятности появления случайной ошибки (или нормального закона распределения вероятностей), в которую входит число 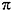
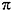
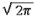
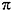
«Замешано» ли число 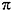
Попробуем разобраться в явлениях, причины которых далеко не ясны, но которые тоже, возможно, не обошлись без числа 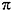
В основе указанных явлений, возможно, лежит так называемый закон распределения максимумов случайных рядов, или «закон троек», сформулированный еще в 1927 году Е. Е. Слуцким.
Число е и однородность времени и пространства
Ясно, что незатухающая волна демонстрирует соблюдение закона сохранения энергии для электромагнитной волны в вакууме. Такая ситуация имеет место при «упругом» взаимодействии волны со средой без потерь ее энергии. Формально это можно выразить так: если перенести начало отсчета по оси времени, энергия волны сохранится, так как у гармонической волны останутся те же амплитуда и частота, то есть энергетические единицы, а изменится лишь ее фаза, часть периода, отстоящая от нового начала отсчета. Но фаза на энергию не влияет именно по причине однородности времени при смещении начала отсчета. Итак, параллельный перенос системы координат (он называется трансляцией) законен в силу однородности времени t. Теперь, наверно, в принципе понятно, почему однородность по времени приводит к закону сохранения энергии.
Далее, представим себе волну не во времени, а в пространстве. Наглядным примером ее может служить стоячая волна (колебания струны, неподвижной в нескольких точках-узлах) или прибрежная песчаная рябь. Математически эта волна вдоль оси О х запишется как e iх =cos х + isin х. Ясно, что и в этом случае трансляция вдоль х не изменит ни косинусоиды, ни синусоиды, если пространство однородно вдоль этой оси. Опять-таки изменится лишь их фаза. Из теоретической физики известно, что однородность пространства приводит к закону сохранения количества движения (импульса), то есть массы, умноженной на скорость. Пусть теперь пространство однородно по времени (и закон сохранения энергии выполняется), но неоднородно по координате. Тогда в различных точках неоднородного пространства оказалась бы неодинаковой и скорость, так как на единицу однородного времени приходились бы различные значения длины отрезков, пробегаемых за секунду частицей с данной массой (или волной с данным импульсом).
Итак, можно сформулировать второй основной тезис:
И все-таки, почему именно число е, а не какое-то другое вошло в формулу Эйлера и оказалось в основании волновой функции? Оставаясь в рамках школьных курсов математики и физики, ответить на этот вопрос непросто. Эту проблему автор обсуждал с теоретиком, доктором физико-математических наук В. Д. Эфросом, и мы попытались пояснить ситуацию следующим образом.
А теперь запишем решение дифференциального уравнения с постоянными коэффициентами, описывающее распространение гармонической волны в среде с учетом неупругого взаимодействия с ней, приводящего к рассеянию энергии или же к приобретению энергии от внешних источников:
f(t) = e (α+ib)t = e αt (cos βt + isin βt).
Сформулированный принцип математически выглядит так: ∆I
Этому закону подчиняются зрение, слух, обоняние, осязание, вкус, эмоции, память (естествен но, пока физиологические процессы не переходят скачком в патологические, когда рецепторы подверглись видоизменению или разрушению). Согласно закону: 1) малому приросту сигнала раздражения в любом его интервале отвечает линейный прирост (с плюсом или минусом) силы ощущения; 2) в области слабых сигналов раздражения прирост силы ощущения гораздо круче, чем в области сильных сигналов. Возьмем для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками. Динамический диапазон биологических рецепторов колоссален: принимаемые глазом сигналы могут различаться по силе в
Следствие 2. Наличие только мнимой части функции при α = 0, β 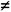
Это следствие возвращает нас к уже рассмотренной выше модели.
Положение о связи законов сохранения с однородностью времени и пространства, бесспорно, правильно для евклидова пространства в классической физике и для псевдоевклидова пространства Минковского в Общей теории относительности (ОТО, где четвертой координатой служит время). Но в рамках ОТО возникает естественный вопрос: а как обстоит дело в областях огромных гравитационных полей, вблизи сингулярностей, в частности, у черных дыр? Мнения физиков здесь расходятся: большинство считают, что указанные фундаментальные положения сохраняются и в этих экстремальных условиях. Однако есть и иные точки зрения авторитетных исследователей. И те и другие работают над созданием новой теории квантовой гравитации.
Фундаментальные константы нашего мира, о природе которых мы говорили, известны не только физикам, но и лирикам. Так, иррациональное число 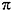
Новое в блогах
Мировые константы π и е в Природе
Всем, кто хотя бы соприкоснулся с математикой, известно, что π – число, равное отношению длины окружности к ее диаметру, а е – основание натуральных логарифмов. Указанные числа входят во множество формул математики, физики, химии, биологии, а также экономики. Это свидетельствует о том, что они отражают некоторые самые общие законы природы. Предлагается популярный анализ мировых констант π и е, основанный на рассмотрении основных свойств пространства и времени.
Число π и сферическая симметрия пространства
Название числа π произошло от греческого π εριφερεια – окружность. Последняя представляет собой множество точек, лежащих на периферии по отношению к центральной точке, а вернее – находящихся от нее на одинаковом расстоянии, называемом радиусом. В то же время сухая формула из математического анализа, позволяющая вычислить число π с любой точностью так определяет это число:
Здесь представлен знаменитый ряд Лейбница (есть и другие ряды). Однако уловить физический смысл π и связь его с окружностью по этой формуле довольно трудно. Между тем особая роль окружности в пространстве нашей Вселенной вытекает из одинаковости свойств пустого эвклидова пространства по любому направлению, то есть изотропности пространства. Это можно пояснить так: для наблюдателя в идеальном изотропном пространстве линия горизонта – окружность. А окружности с данными центром и радиусом составляют сферу. В теоретической физике именно с этим свойством связан закон сохранения вращательного момента. Отсюда же вытекают общеизвестные следствия.
Первое. Длина дуги окружности, в которой умещается ее радиус, составляет естественную дуговую и угловую единицу – радиан (рад). Эта единица безразмерная. Чтобы найти число радианов в дуге окружности, надо измерить ее длину и разделить на длину радиуса (допустим, в метрах, которые при делении сокращаются).
Величина вероятности попадания в круглую мишень (R – радиус) при прицеливании в центр (0) круга отложена вверх по оси z. Она может быть вычислена для любого отклонения (х) от центра с помощью
формулы Гаусса φ(x) =
Число π отражает равноправность случайных отклонений по всем направлениям в сферически симметричном пространстве.
Вдоль любой полной окружности ее радиус укладывается приблизительно 6,28 раза. Точнее, полная дуга содержит 2 π радианов.
Второе. Предназначение тригонометрических функций – выражать соотношения между дуговыми и линейными размерами объектов, а также между пространственными параметрами процессов, происходящих в сферически симметричном пространстве. Из сказанного ясно, почему аргументы тригонометрических функций (синуса, косинуса, тангенса) в принципе безразмерны, как и у других типов функций, то есть эти действительные числа – точки на числовой оси. Градус же на ней – доля единичного безразмерного отрезка, равного радиану, и потому он не имеет размерности.
Далеко не каждый сможет, не пользуясь калькулятором, правильно ответить на вопрос, чему равен cos 1 (это приблизительно 0,5), или на несколько более сложный – чему равен arctg ( π /3). Последний пример особенно сбивает с толку. Часто говорят, что это бессмыслица: «Чему равна дуга, арктангенс которой равен 60°?» Если сформулировать вопрос именно так, то ошибка заключается в применении градусной меры к аргументу арктангенса. Правильный ответ получится, если аргумент выражать в радианах: arctg (3.14/3) ≈ arctg 1 = π /4 ≈ 3/4. Еще одно замечание. К сожалению, сплошь и рядом абитуриенты и студенты считают, что π = 180°. Приходится их поправлять: π = 3,14. Но, конечно, можно сказать и так; π радианов равно 180°.
Нетривиальная ситуация встречается и в теории вероятностей. Она касается нормального (гауссовского) закона распределения вероятностей и важной формулы вероятности случайной ошибки (или случайного отклонения), в которую входит число π . Откуда оно тут появилось? Как вероятность связана с окружностями? Наглядной иллюстрацией ответа на этот вопрос служит пример со стрельбой по мишени в неизменных условиях. Дырочки на мишени рассеяны по кругу (!), так как стрельба происходит в сферически симметричном пространстве, в котором равновероятны случайные отклонения по любым направлениям. Теперь понятно, почему вероятность попадания в круг с центром в центральной точке мишени и любым заданным радиусом вычисляется по формуле, содержащей число л.
По первой букве фамилии Эйлер
Формула для вычисления другой мировой константы, е, выглядит так:
Обратимся к распространению электромагнитных волн в вакууме. Причем вакуум мы будем понимать как классическое пустое пространство, не касаясь сложнейшей природы физического вакуума.
Леонард Эйлер (1707-1783), один из величайших математиков. Родился в Швейцарии. В 1727-41 гг. жил и работал в России, член Петербургской академии наук. В его честь по первой букве фамилии Euler названо число е – основание натуральных логарифмов.
Сначала Эйлер нашел формулу еiπ = – 1. В ней впервые число возводилось в мнимую степень (!), что явилось, кстати, следствием соединения чисел π и е. Результат, казавшийся поначалу крайне непривычным, не имеющим отношения к реальности (почему числа и были названы мнимыми), оказался очень удобным для математического моделирования циклов движения по окружности, а следовательно, и для гармонических колебаний. Действительно, что будет, если колебательному движению маятника сообщить толчком второе колебательное движение в перпендикулярном направлении? Окончание маятника будет описывать окружности, если амплитуды обоих колебаний одинаковы. Но круговое движение станет возможным, только если второе колебание сдвинуто по фазе относительно первого колебания на полпериода, как сдвинута синусоида относительно косинусоиды. Ведь в момент наибольшего отклонения маятника по одной координате он имеет нулевое отклонение по перпендикулярной координате. И если на первой координатной оси отсчитывать действительные числа, то на второй координатной оси можно одновременно отсчитывать числа в том же масштабе, но это будет уже новое числовое множество. Оно-то и было названо множеством мнимых чисел, за единицу которых принята мнимая единица, обозначенная буквой i (imaginaire, франц. – мнимый, воображаемый).
Формулу Эйлера нужно пояснить, ибо в наше время из обычных школьных программ исключены комплексные числа. Комплексное число z = х + iy состоит из двух слагаемых – действительного и мнимого чисел. Последнее представляет собой действительное число у, умноженное на мнимую единицу i = √( – 1). Действительные числа откладывают вдоль действительной оси Ох, а мнимые – в том же масштабе вдоль мнимой оси Оу, единицей на которой служит i. Длина единичного отрезка есть модуль | i | = 1. Комплексному числу соответствует точка на плоскости с координатами (х, у). Физический смысл необычного вида числа е с показателем, содержащим только мнимые единицы i, означает движение точки по окружности цикл за циклом. Это равносильно колебаниям, описываемым сложением косинусоиды и синусоиды с постоянными и равными амплитудами, то есть незатухающим колебаниям.
Ясно, что в любой незатухающей волне соблюдаются законы сохранения энергии и импульса (количества движения), например, при прохождении звуковой волны в идеально упругой среде или электромагнитной волны в вакууме. Ситуацию можно строго сформулировать так. Если сместить начало отсчета по оси времени (момент наблюдения), то энергия волны не изменится, так как гармоническая волна сохранит ту же амплитуду и частоту (это энергетические единицы), изменится лишь фаза волны, то есть часть периода, отстоящая от нового начала отсчета (фаза не связана с энергией). Значит, параллельный перенос системы координат (он называется трансляцией) вдоль оси времени инвариантен для незатухающей волны в силу однородности времени t. Это и поясняет связь однородности времени с законом сохранения энергии.
Аналогично можно переносить систему вдоль оси пространственной координаты: для незатухающей волны не изменится ничего, кроме фазы. Сохранится и количество движения – импульс, который несет волна. Из теоретической физики известно, что однородность пространства приводит к закону сохранения импульса. Что такое импульс частицы? Это масса, умноженная на скорость. Представим себе, что пространство однородно по времени (и закон сохранения энергии выполняется), но неоднородно по какой-либо координате. Тогда в различных точках неоднородного пространства оказалась бы неоднородной и скорость, так как на единицу однородного времени приходились бы различные значения длины отрезков, пробегаемых за секунду частицей с данной массой (или волной с данным импульсом).
Итак, число е как основание функции комплексного переменного связано с законом сохранения энергии в замкнутой системе, который обусловлен однородностью времени, и с законом сохранения импульса, который обусловлен однородностью пространства.
И все-таки, почему именно число е, а не какое-то другое, вошло в формулу Эйлера и оказалось в основании волновой функции? Оставаясь в рамках школьных курсов математики и физики, ответить на этот вопрос непросто. Линейные и линеаризованные процессы сохраняют свою линейность именно благодаря однородности пространства и времени. Математически линейный процесс описывается функцией, которая является решением дифференциального уравнения с постоянными коэффициентами (ДУПК). Ядро такой функции – приведенная выше формула Эйлера, то есть функция комплексного переменного с основанием е, или уравнение волны.
Почему именно е, а не другое число находится в основании функции, которую ищут как решение данного уравнения волны в виде ДУПК? Да потому, что только функция еt не изменяется при любом числе дифференцирований и интегрирований. А это нужно, чтобы после подстановки в уравнение его решения оно превратилось в тождество. Действительно, в исходное ДУПК подставляют функцию еt и все ее производные. С математической точки зрения, постоянные коэффициенты при экспоненте «не мешают» при дифференцировании, оставаясь теми же, а все еt сокращаются, приводя к алгебраическому уравнению. Корни последнего входят как постоянные коэффициенты в экспоненту и приводят ДУПК к требуемому тождеству. С физической же точки зрения, коэффициенты в волновом уравнении (и ему подобных) в форме ДУПК постоянны, потому что постоянны законы протекания процессов в однородном времени – пространстве. Для наблюдателя, находящегося в системе отсчёта, сдвинутой по времени или по координате относительно исходной системы отсчета, физический процесс должен описываться уравнениями того же вида, что и исходные уравнения, если время и пространство однородны. Но вместе с тем (после сдвига наблюдателя) в исходных уравнениях появятся сдвиги аргументов по времени (t + t0) и координатам (х + х0) Будет ли начальное уравнение равносильно уравнению со сдвинутыми аргументами? Да, будет при условии постоянства коэффициентов при функции и ее производных, входящих в ДУПК, описывающее процесс. Ведь именно они, состоя при экспоненциальной функции, дают верное решение, превращая уравнение в тождество. Вот почему число е играет столь важную роль в гармонических волновых процессах, описываемых законами естествознания!
Коснемся случая затухающей волны. Решение ДУПК, описывающее распространение гармонической волны в среде, если в ней происходит рассеяние энергии, будет, естественно, несколько сложнее, чем для волны без затухания. В показателе степени экспоненты вместо мнимого числа iβ, отражающего чисто волновой процесс, появляется комплексное число α +iβ, где действительное число α отрицательно и отражает затухание волны:
f(t) = e ( α +i β )t = e α t (cos α t + i sin β t). Здесь формула Эйлера умножена на действительную переменную величину eαt, которая играет роль убывающей амплитуды волны.
А теперь положим β = 0, то есть уничтожим колебательный множитель. От колебаний останется только затухающая по экспоненте интенсивность – «бывшая амплитуда». Для иллюстрации обоих случаев представим себе маятник. В пустом пространстве он колеблется без затухания. В пространстве с сопротивляющейся средой колебания происходят с амплитудой, убывающей по экспоненте. Если отклонить маятник в достаточно вязкой среде, то он будет плавно, без колебаний двигаться к положению равновесия, все более замедляясь. То же произойдет с грузом, прикрепленным к стенке достаточно слабой пружиной в весьма вязкой среде. После отклонения груз будет плавно двигаться к положению равновесия.
а) Незатухающая гармоническая волна с амплитудой А, частотой β и фазой φ0, иллюстрирующая закон сохранения энергии, связанный с однородностью времени. Перенос системы координат вдоль оси t, не изменяющий энергетических характеристик волны (ее амплитуды и частоты), возможен в силу однородности времени. При переносе изменяется только фаза (неэнергетическая характеристика). Закон сохранения импульса, связанный с однородностью пространства, иллюстрируется такой же волной, если в ней временную координату (t) заменить на пространственную (х).
б) Затухающая волна в среде, в которой энергия волны рассеивается. Амплитуда волны убывает по экспоненте. В очень вязкой среде колебания прекращаются, остается только плавно убывающая амплитуда α (
Рассмотренный предельный частный случай «волны» с нулевой частотой, но с плавно изменяющейся (убывающей или возрастающей) по экспоненте «амплитудой», характеризует множество процессов в самых различных сферах неживой и живой природы: рост снежного кома, моллюска, финансовой пирамиды, остывание чайника, убывание памяти со временем, увеличение числа бактерий в организме, физиологическая зависимость ощущения от силы раздражения и т.д. Всеми этими разнородными явлениями «управляет» экспонента, или, иначе говоря число е, стоящее в основании показательной функции. Ибо все эти процессы подчиняются одному и тому же фундаментальному принципу: прирост величины пропорционален самой величине.
Универсальный психофизический закон
Остановимся подробнее на универсальном психофизическом законе Вебера-Фехнера, чрезвычайно важном для всего живого на Земле. (Густав Теодор Фехнер (1801-1887), немецкий физик; Эрнст Генрих Вебер (1795-1878), немецкий физиолог.) Закон гласит: «Сила ощущения пропорциональна логарифму силы раздражения». Этому закону подчиняются зрение, слух, обоняние, осязание, вкус, эмоции, память (естественно, пока физиологические процессы не переходят резко в патологические, то есть пока рецепторы не подверглись видоизменению или разрушению). Из закона Вебера-Фехнера следует, что, во-первых, малому приросту сигнала раздражения в любом его интервале отвечает почти линейный прирост (с плюсом или минусом) силы ощущения и, во-вторых, в области слабых сигналов раздражения прирост силы ощущения гораздо круче, чем в области сильных сигналов.
Логарифмическая зависимость силы ощущения от силы раздражения (универсальный психофизический закон Вебера-Фехнера). За порог обнаружения сигнала принято давление звука р0, едва ощущаемое человеком. На пороге слышимости (р = р0) натуральный логарифм единицы
Приведем такой пример. Чай с двумя кусками сахара воспринимается как в два раза более сладкий, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с десятью. Динамический диапазон биологических рецепторов колоссален: принимаемые глазом сигналы могут различаться в
1010, а ухом – даже в 1011 раз. Живая природа вынуждена была приспособиться к таким диапазонам. В процессе эволюции она защищалась, учась логарифмировать поступающие раздражители. Это делалось путем различных биологических способов демпфирования и диафрагмирования сигналов, иначе рецепторы сразу погибли бы.
Раковина моллюска растет по закону натуральной логарифмической спирали, который оптимален для организма. Она описывается уравнением r = аеφ. В основании степени стоит число е. Здесь r есть радиус-вектор? φ – угол между ним и горизонтальным направлением вправо. Спираль пересекает радиусы-векторы под одним и тем же углом μ, почему и называется равноугольной. По аналогичной спирали расположены семечки в подсолнухе и чешуйки в шишках.
На законе Вебера-Фехнера основана широко применяемая логарифмическая шкала силы звука в децибелах (дБ), в соответствии с которой изготовляют регуляторы громкости аудиоаппаратуры: в них смещение рычага пропорционально ощущаемой громкости, но не силе звука! Ощущение пропорционально lg p/p0. За порог слышимости принято давление звука р0 = 10-12 Дж/м2с. На пороге имеем lg1= 0. Увеличение силы (давления) звука в 10 раз соответствует примерно ощущению шепота, которое выше порога на 1 бел (Б) по логарифмической шкале. Усиление звука в миллион раз (от шепота до крика), до
10-5 Дж/м2с, по логарифмической шкале есть увеличение на 6 порядков, то есть на 6 Б.
Барабанная перепонка легко переносит подобный перепад давления именно благодаря тому, что ощущение реагирует на него гораздо слабее, чем при прямой пропорциональной зависимости. Логарифмическая зависимость быстро ослабевает и потому менее опасна для рецепторов. Их разрушает лишь усиление звука в 10 млрд. раз.
Другой, не менее яркий пример. Шкала звездных величин определена так, что блеск звезды Е связан со звездной величиной m формулой
m = – 2.5 lg E + const.
Эта формула – прямое следствие закона Вебера-Фехнера. Ощущение (звездная величина) пропорционально логарифму раздражения (в данном случае, лучевой энергии звезды). Поэтому разность в пять звездных величин соответствует различию в блеске звезды ровно в 100 раз. Экспоненциальный (по прямой функции) и логарифмический (по обратной функции) законы прироста величин оптимальны для развития многих организмов. Их действие можно наглядно проследить по образованию логарифмических спиралей в раковинах моллюсков, рядах семечек в подсолнухе, чешуек в шишках.
Фундаментальные константы нашего мира, о природе которых мы говорили, известны не только физикам, но и лирикам. Так, иррациональное число π , равное 3,14159265358979323846. вдохновило выдающегося польского поэта XX в. лауреата Нобелевской премии 1996 г. Виславу Шимборскую на создание стихотворения «Число Пи», начальными строками которого мы закончим эти заметки.
π – число, достойное восхищения:
Три запятая один четыре один.
Каждая цифра дает ощущение
начала – пять девять два, ведь до конца не дойти никогда.
Взглядом всех цифр не объять – шесть пять три пять.
Арифметических действий – восемь девять –
уже не хватает, и трудно поверить – семь девять –
что не отделаться – три два три восемь –
ни уравнением, которого нет,
ни шутливым сравнением – оных не счесть.
Двинемся дальше: четыре шесть.
(Пер. с польского Б. Горобца)
Существуют ли стихи о числе е, нам не известно.