Что такое exp в формуле

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Что такое экспонента в математике для чайников

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Узнайте также, что такое Число Пи и Логарифм.

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Понятие экспоненциального роста

Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:

И выглядит это примерно так:

Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.

Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:

Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:

Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

Приглядимся поближе

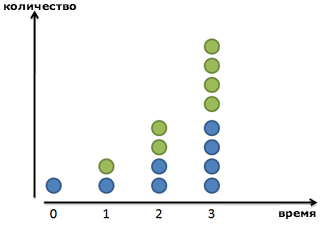
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

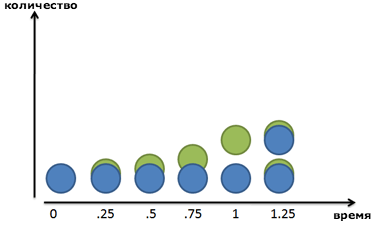
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Источник

Число Эйлера (e)

Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.

Способы определения числа e (формула):

1. Через предел:

Второй замечательный предел:

Альтернативный вариант (следует из формулы Муавра – Стирлинга):

2. Как сумма ряда:

Свойства числа e

1. Предел обратного числа e

2. Производные

Производной экспоненциальной функции является экспоненциальная функция:

Производной натуральной логарифмической функции является обратная функция:

3. Интегралы

Неопределенный интеграл натуральной логарифмической функции log_e x:

Определенный интеграл от 1 до e обратной функции 1/x равен 1:

Логарифмы с основанием e

Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:

Экспоненциальная функция

Это показательная функция, которая определяется следующим образом:

Формула Эйлера

Комплексное число e iθ равняется:

Источник

Экспоненциальный график в excel

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

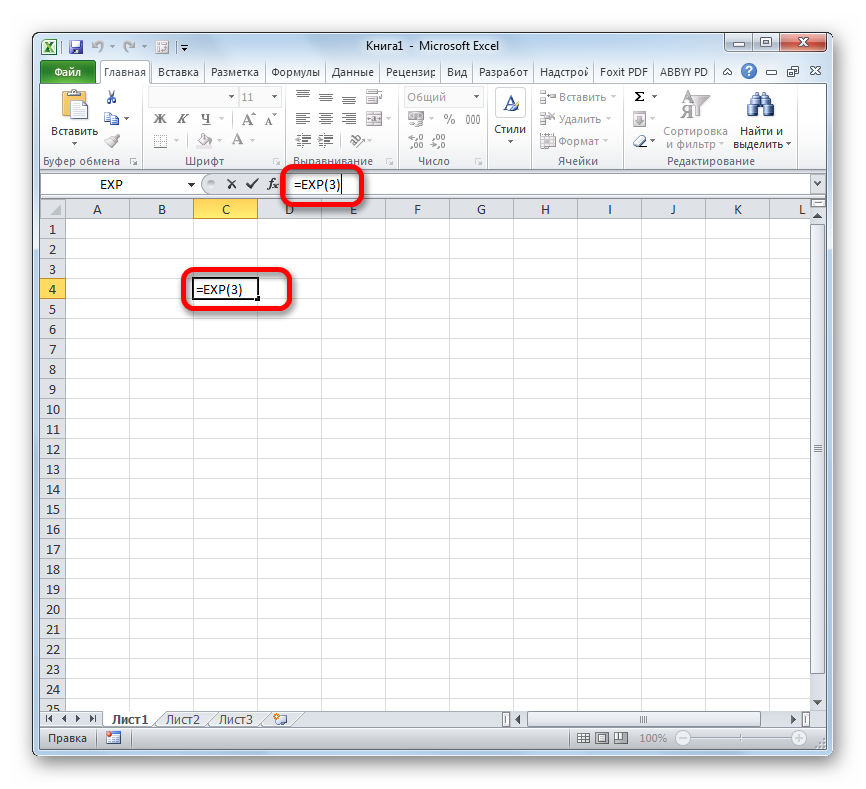
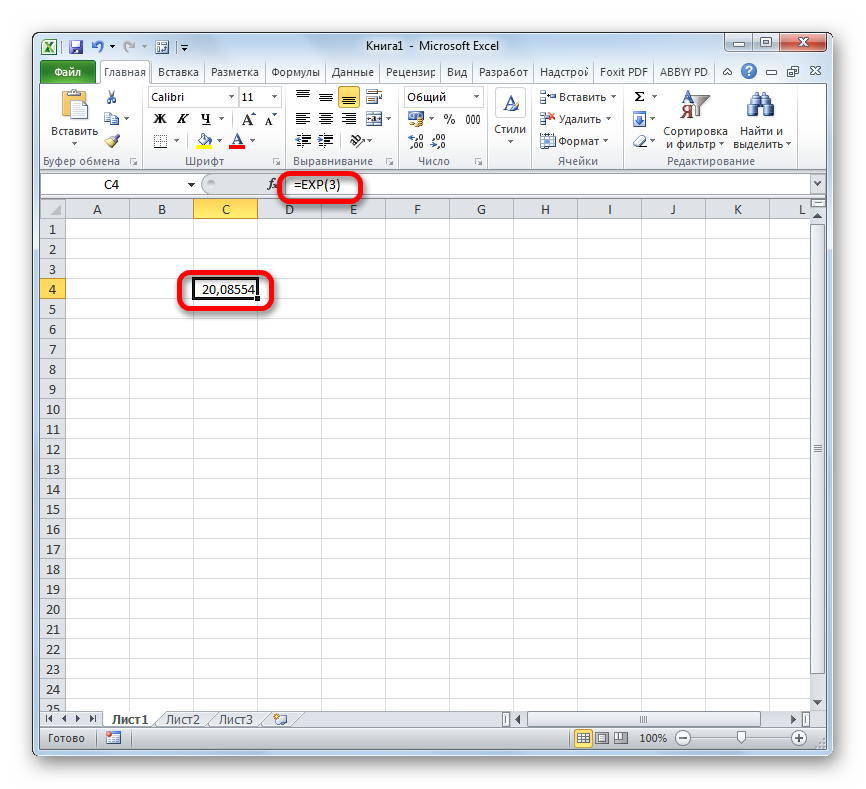
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.

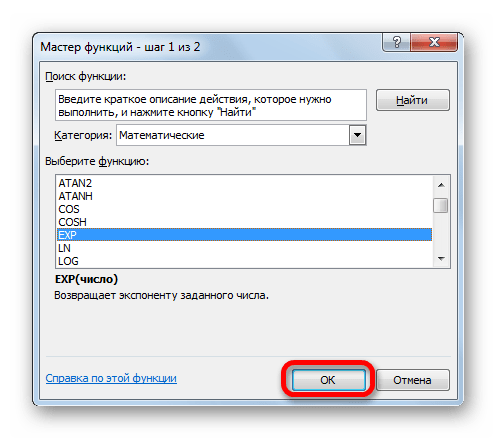
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».

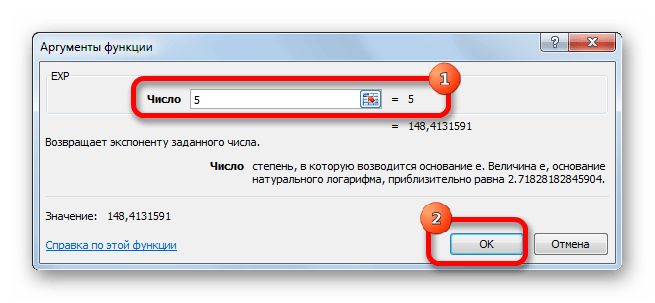
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».

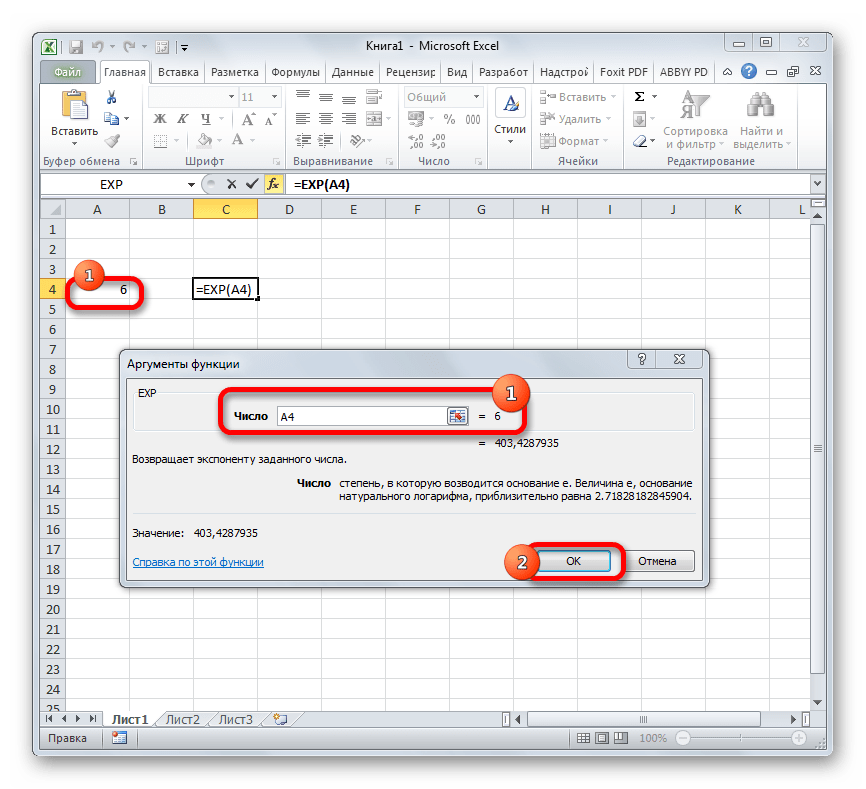
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

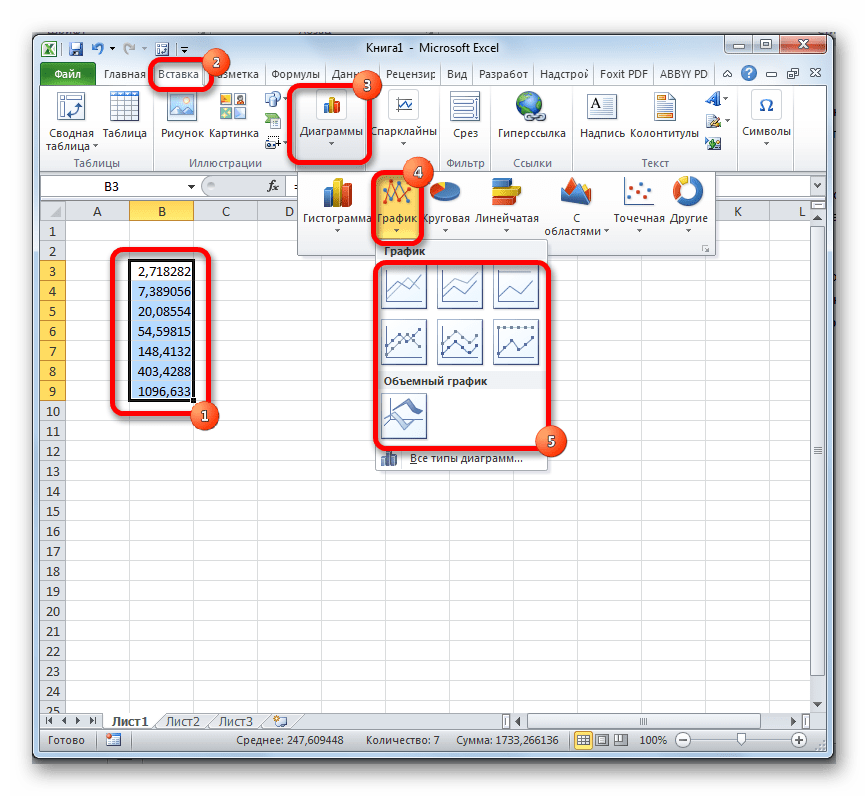
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Excel работает за вас

Excel works!

Thanks for Visiting

Экспонента в Excel. Что такое экспонента и как применять?

Экспонента. Что это такое?

Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:

Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).

Что это вообще такое, и что для нас означает?

Лучше всего, действие экспоненты показывают графики ниже:

Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:

Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.

Кстати население на планете Земля тоже растет по экспоненте;)

Принцип Парето и экспонента

Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:

20% любителей пива употребляют 80% всего пива

На принципе Парето построен и ABC анализ запасов, например.

Этот принцип Парето — еще один пример экспоненты.

Кстати очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.

При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:

Экспонента в Excel

Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.

В Эксель все посчитать несложно:

или можно число возвести в степень

Дополнение. Как запомнить 15 знаков числа е?

В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков

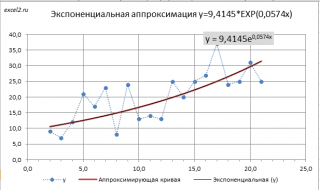
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.

Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК – МНК: Метод Наименьших Квадратов в MS EXCEL.

В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:

В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).

Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.

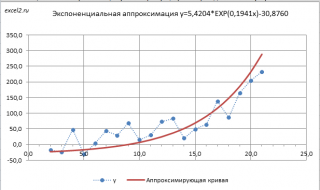
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.

Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).

Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).

Функция РОСТ()

Синтаксис функции следующий:

РОСТ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])

Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y) и на массив значений переменной Х (аргумент известные_значения_x). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).

Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.

Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.

Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y=a*EXP(b*x).

Чтобы вычислить коэффициент b используйте формулу:

= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))

Функция ЛГРФПРИБЛ()

Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y=a*m^x.

Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).

Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:

= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) – коэффициент b

= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) – коэффициент a

Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).

Источник