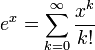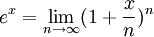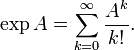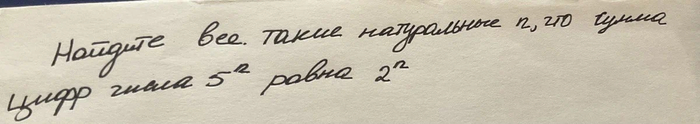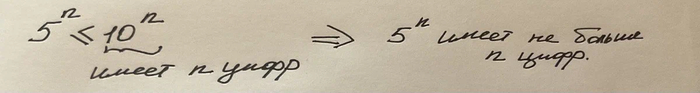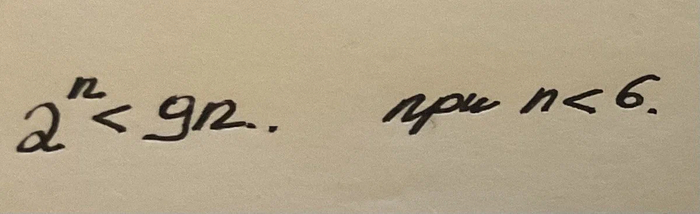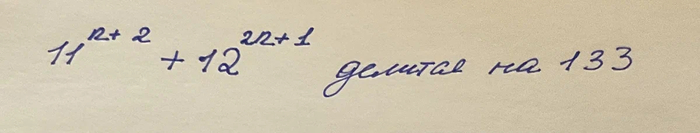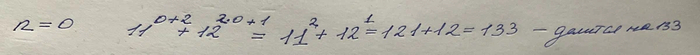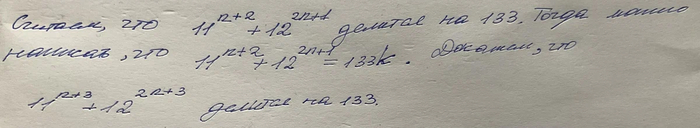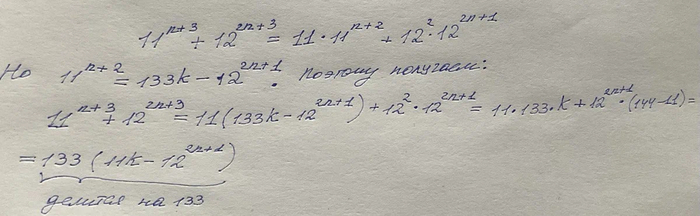Что такое exp в математике

Экспоненциальная функция

Содержание

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

Свойства

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

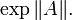
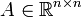
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 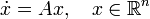с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :

См. также

Полезное

Смотреть что такое «Экспоненциальная функция» в других словарях:

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь

экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика

экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь

экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas

Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь

экспоненциальная — функция [ Словарь иностранных слов русского языка

Источник

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

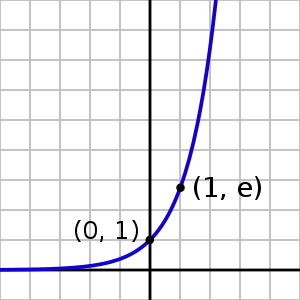
График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Что такое экспонента в математике для чайников

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Узнайте также, что такое Число Пи и Логарифм.

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Понятие экспоненциального роста

Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:

И выглядит это примерно так:

Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.

Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:

Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:

Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

Приглядимся поближе

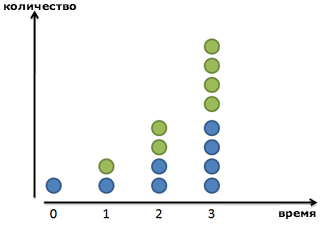
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

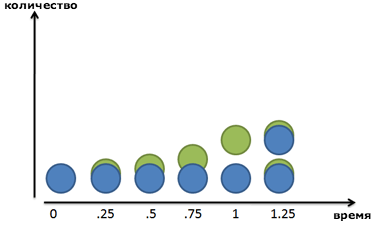
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Источник

Экспонента в жизни- 2. Зачем это нужно?

В прошлом посте мы говорили о том, как пролетели австралийцы с экспонентой.

В этом – постараюсь ответить на главный вопрос жизни Вселенной и все такое.

Где математика экспонента может пригодиться в реальной жизни?

Можно, конечно, скорчить серьезную физиономию и сказать, что,мол:

По экспоненте высыхает земля после дождя, по экспоненте падает давление, когда вы поднимаетесь в горы…. но звучит это как-то по-ботански!

Мало, кто считает диаграммы, придя домой.

Открою страшную тайну:

Вряд ли в жизни придется услышать такое:

— Дайте мне (7! – 6^2+3e^0)^1/4 помидоров и (ln (e^3) ) картофеля, пожалуйста.

— Молодой человек, я не понимаю.

— Мне плевать, я учился не напрасно.

Да, сами по себе занятия математикой неплохо качают мозги (об этом в следующих постах)

То экспонента вам в жизни не понадобится…

Вообще-то, есть одна тема, где понимание экспоненты может помочь. Тема, с которой сталкиваются все.

Она может помочь в мегаважном вопросе –

Положили вы в банк 1000 рублей под 10 процентов годовых.

То есть, за год вклад увеличится в 1,1 раза.

Через год будет 1000*1,1 =1100. Небольшая прибыль за то, чтобы отдать кому-то свои кровные.

А если надолго? Тоже мелочь какая-то, вложить лет на 30 и получить что, 3000 сверху? Да нафига?

Вот здесь останавливается большая часть людей которые задумались над тем чтобы как-то преумножать доходы. Но проблема то в том что считается все по-другому!

Но вот тут-то фишка работает по-другому. Ведь в следующий раз проценты начисляются от нового вклада, от 1100

1000*1,1^2 =1221 а не 1200. Вообще, кажется, мелочь, но это не так.

За 30 лет вклад увеличится в 17 раз, а за 40 – в 45!

А если вкладывать под 20 процентов то вклад увеличится в 40 раз уже за 20 лет

Вроде разница не очень велика, но чем дольше вкладываете, тем круче рост.

Не какая-то там примитивная линейная функция или тормознутая парабола, график растет Экспоненциально. Даша, напомни, пожалуйста.

Это ярче всего описывает история, как индейцы продали остров Манхеттен буквально за бусы.

Но, все не так однозначно.

Если бы индейцы положили в банк 30 баксов под 6 процентов годовых, то за 400 лет получили бы почти 400 млрд долларов!

30*1,06^400 = 397 619 212 307

И могли бы скупить весь Манхеттен на корню вместе со всем содержимым.

Есть ощущение, что к этому моменту народ постарше начинает кипеть

Тут есть важный нюанс – все это работает, если экономика и государство находятся в худо-бедно стабильном и рыночном состоянии.

Например, в США частенько были проблемы с финансами и гиперинфляцией. Так в 1865 г., после Гражданской войны, сбережения многих вкладчиков банков резко обесценились и стали мизерными. 150 лет назад.

Ну и по мелочи – 1998, 2014

Но страна-то сменилась. И теперь можно делать стандартные для инвестиций штуки, чтобы минимизировать риски: диверсификация активов, инвестирование в разных валютах и в компании разных стран.

Чтоб, если и профукать все деньги, то только, если вся Земля разом обанкротится.

А вместе оно веселей.

Да,много сложностей- и учиться инвестициям,и опасности- пирамиды, санация банков, падение рынка. Поэтому, кстати и не говорю про проценты более 20 в год- там са-а-а-авсем другие уровни рисков. Но если серьезно сесть и посчитать- 20 процентов в год,если планировать на сколько-нибудь долгий период,очень даже неплохо!

Фонд Уоррена Баффета на протяжении около 50 лет давал среднюю доходность в 20 процентов годовых,. и вот он один из трех самых богатых людей мира, в 2008 и вовсе потеснивший с первого места Билла Гейтса.

Вообще, в европейских странах, не так запуганных этим «Вжух»,

С первой зарплаты народ начинает вкладывать на свадьбу-рождение-обучение детей.

Ну, а что делать, если денег нет? И получить хочется быстрее, чем через 30 лет?

Можно заработать, запустить свое дело.

Но чтобы заработать денег – надо деньги. Стартовый капитал, так его.

Взять его можно у тех, у кого деньги уже есть

Есть более безопасный способ.

Прийти к инвесторам и сказать, дайте денег.

И когда вы пойдете просить денег, вдруг окажется, что права была Марь Петровна, приговаривая

« Учи Сидоров, экспоненту! В жизни пригодится»

Ибо люди, которые дают другим деньги на бизнес, редко когда оказываются совсем уж дебилами.

У дебилов просто не будет много денег. Ну… в теории.

И инвесторов нужно убедить, доказать, что ваш проект – хорошая инвестиция.

И вот тут-то и нужна, оказывается, математика, в том числе, экспонента.

По экспоненте, при хорошей конъюнктуре растут продажи и доход.

Для того, чтобы захватить мир, Макдональдсу оказалось достаточно расти на 15 процентов в год на протяжении 45 лет с 1950 до 1985.

И если бизнес сможет расти по экспоненте хотя бы несколько лет – это уже очень круто.

(то не какая-то абстрактная теория, это вопросы одного из моих взрослых учеников, который запускал новый бизнес. Готовил бизнес-план для представления инвесторам. Математикой занимался «для себя»)

Не всегда это работает, но без четкого плана, как и сколько зарабатывать, денег обычно не дают.

Рост акций Эппл. Похоже?

В общем, экспонента – это классная тема)

Следующий пост – про падающую экспоненту и о том, почему мы не пользуемся искусственным золотом (почти).

*Строго говоря, экспонента – это график e^x, где е

Очень интересно,когда будет про падающую экспоненту?

А какая самая быстрая функция?

МатОлимп №2

Итак, рассмотрим следующую задачу. Формулировка у нее очень простая:

Эта задача была предложена на заключительном этапе олимпиады школьников (Всероссийская олимпиада 1993 года). Задача на 5 из 10.

Для решения заметим следующий факт:

Так как максимальная цифра у нас 9, значит сумма всех цифр нашего числа не превышает 9n. Но вообще-то:

Попробуйте доказать это утверждение самостоятельно.

К сожалению, при n>=6 это неравенство нарушается. Поэтому мы понимаем, что условие задачи невозможно при n>=6, иначе мы придем к противоречию с самым первым фактом в нашем решении.

Итак, мы пришли к тому, что нам достаточно рассмотреть в качестве n одно из чисел <1,2,3,4,5>.

1) n = 1. Число 5 имеет сумму всех чисел 5 и это не равно 2.

2) n = 2. Число 25 имеет сумму чисел 7 и это не равно 4.

3) n = 3. Число 125 имеет сумму чисел 8 и совпадает с 2*2*2. Бинго! Одно из чисел найдено!

4) n = 4. Число 625 имеет сумму чисел 13 и не совпадает с 16.

5) n = 5. Число 3125 имеет сумму 11 и не совпадает с 32.

На этом перебор заканчивается, так как мы отбросили все числа после 5. Единственное такое натуральное число это 3.

Очередная задача решена, город будет спать спокойно)

Давайте рассмотрим задачу, которая предлагалась на Московской олимпиаде 1955 года

Добрый день! Сегодня мы с вами разберем задачу, которая предлагалась на Московской олимпиаде 1955 года. Само задание не очень сложное, по ощущениям на 4 из 10.

Для доказательства этого утверждения нам понадобится принцип математической индукции.

Итак, покажем, что наше утверждение верно для n=0.

Теперь предположим, что наше утверждение верно для произвольного номера и покажем, что оно верно для следующего номера. В математической формулировке это утверждение имеет вид:

Итак, мы на финишной прямой. Доказав делимость выражения выше на 133, наше доказательство по индукции будет окончено.

Задача решена! Теперь можно идти и со спокойным сердцем пить чай)

Вероятность

Как Пифагор «придумал» музыку и музыку ли он придумал? 😉 Как возникла современная музыкальная система и как в её звуки связаны между собой? Почему нот семь, а на фортепиано семь белых и пять черных клавиш? Где об этом можно прочитать подробнее?

Сколько книг влезет в килограмм флешек?

На флешку можно записать 500 часов непрерывного листания этих книг. (1 ТБ microSD-карта)

Пусть будет 4 байта. В 1 Тб будет:

1 024 Гб = 1 048 576 Мб = 1 099 511 627 776 байт. 1 трлн байт.

Или от 0,25 до 1 трлн символов.

Самая большая в мире библиотека расположена в Вашингтоне. И это библиотека конгресса США. На ее счету более 155 миллионов экземпляров книг на 470 языках!

В Библии 3 172 512 буквы.

Если в книге 1 млн символов, включая знаки препинания и пробелы, тогда на флешку поместится 250 млрд символов или 250 тыс книг.

Вес флешки microSD около 1 грамма.

Кило флешек позволит таскать 250 млн книг, в каждой по 1 млн символов и с учетом самого худших случаев кодирования (4 байта/символ). Для однобайтовой кириллицы 1 млрд книг.

Получается, что даже ребенок может поднять знания, которые хранятся в библиотеке конгресса США.

Средняя скорость чтения взрослого человека около 1500 символов в минуту (200-250 слов в минуту). Данные из сети.

В 1 кг терабайтовых флешек содержится 250-1000 трлн символов или 0,25-1 трлн символов/флешка. Далее считаю для 250-1000 трлн символов:

Взрослый человек потратит на чтение 166-666 млрд минут. 525 960 минут в году.

При 8 часов в день 40 часов в неделю, 50 недель в год (остальное на отпуск), 25 лет стажа будет времени:

40*50*25*60 = 3 000 000 минут.

Понадобится нанять на чтение от 55 556 до 222 222 человек. Чтобы они каждую рабочую минуту просто читали текст с одного кг флешек по одому ТБ каждая.

Или от 56 до 222 человек на чтение одной флешки в один ТБ.

Или просто поставить девять копий Red Dead Redemption 2 — 112 ГБ.

спасибо всем за дополнительную информацию.

К примеру архив библиотеки Либрусек по состоянию на 18 июля 2021 составляет 384.675 книг и весит 250 гб.

250 млрд байт / 384 675 книг = примерно 650 кб занимает средняя книга Либрусека.

Я брал значение от 1 до 4 Мб. Т.е. заранее учел замечание @Drnikeriwera

А если учесть спецсимволы (математику вспомним) и непечатные символы необходимые для редактирования? Не будем же мы читать сплошной текст.

Но автор не учел сжатия, даже простой зип даст огромное сжатие на обычном тексте.

Это информационный пост про моего дедушку, прошу вашей помощи в распространении, комментарии для минусов как всегда прилагаю.

Благодаря силе Пикабу у дедушки не только набралось достаточное количество учеников, но и даже переполнилась группа! Здесь я хочу поблагодарить всех, кто лайкнул, кто прокомментировал тот пост и кто пришел на занятия. Спасибо вам!

(В августе, кстати, новый набор, если кому интересно и нужно. Но сейчас не об этом.)

В комментариях к тому посту многие советовали завести канал и обучать онлайн. Тогда дедушка всячески отнекивался, не до того, не умеет, нет времени и т.д.

А в том году вскоре после начала пандемии я неожиданно узнал, что дедушка резво осваивает ютуб, проходит (зачем-то) курс по фотошопу, читает про продвижение на ютубе и все прочее, на что мой папа ворчит не переставая… 🙂

И вот теперь у него есть свой ютуб-канал. Вот ссылка

Он его ведет сам, жена только немного помогала с обложками для видео.

Все ролики он долго и мучительно монтирует сам, подбирая фото и музыку (на что папа ворчит еще больше). Поэтому не судите строго. Но ему очень важно сделать все самому, самому во всем разобраться и сделать так, как сам видит. И постепенно улучшает качество видео.

В каждом видео дедушка соединяет поэзию и математику, решая математическую задачу с различными персонажами.

«В наше жестокое время, в эпоху резкого расслоения общества автор пытается

рассказать нам не только о математике – отсюда такая, несколько необычная

форма подачи материала и соединение, казалось бы, несоединимого –

математики и поэзии.» (Описание от дедушки)

Как он сам мне писал: «Это не математика, хотя название такое.

Всего лишь Истории, где есть и о математике…»

(А еще недавно деда даже сделал курсовую по межпредметной интеграции математики и поэзии.)

Что касается канала, то он создан для школьников всех возрастов и взрослых. В основном, для 5-7 классов. Поскольку это основная, по мнению автора, беда.

Дедушка очень переживает, поймут ли правильно его и его видео, но хочет вести канал именно в таком формате. Так лежит его душа.

И в заключение привожу его прямую цитату:

«Надо прямо сказать о моём отношении к тому, что случилось с системой образования в целом. Автор считает, что за последние 30 лет, традиционная советская система образования безжалостно уничтожена. Не вдаваясь в детали, и понимая беспомощность одного любого человека в целом, он хочет помочь ТЕМ родителям, бабушкам и дедушкам, которые в буквальном смысле должны не заменить собой существующую школу, но всячески помочь ей. Нужно последовательно, очень медленно и методично помогать ребенку в получении знаний. Сегодня же, в школе приветствуются только, так называемые проектные работы, интегрированное обучения начинается едва ли не с 1 класса. едва ли не с этого же времени начинается подготовка к абсолютно обанкротившейся системе ОГЭ и ЕГЭ.

Дважды в неделю в течение учебного года автор проводит вечерние дистанционные занятия с родителями своих учеников. Занятия бесплатные. На канале НЕСТРАШНАЯ МАТЕМАТИКА и ПЕСНЯ.

Источник