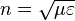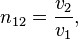Что такое абсолютный и относительный показатели преломления
Абсолютный и относительный показатели преломления в физике
Абсолютный и относительный показатели преломления
Показатель преломления (коэффициент преломления) — это оптическая характеристика среды, связанная с преломлением света на границе раздела двух прозрачных, оптически однородных и изотропных сред при переходе из одной среды в другую и связанная с различием скоростей распространения света 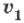
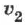
Величина показателя преломления, равная соотношению этих скоростей 
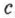
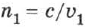
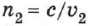
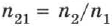
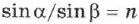
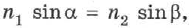
где 
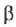
Среда, в которой скорость света больше, называется оптически менее плотной. Таким образом, при переходе из оптически менее плотной среды в оптически более плотную 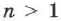
Абсолютный показатель преломления зависит от природы и строения вещества, его агрегатного состояния, температуры, давления, наличия в нём упругих напряжений. Показатель преломления данной среды зависит от длины волны света. Для большинства прозрачных жидкостей и твёрдых тел показатель преломления в видимой области в среднем равен 1,5.
Абсолютный показатель преломления воздуха для жёлтого света при нормальных условиях равен 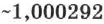
Эта лекция взята со страницы лекций по всем темам предмета физика:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Показатель преломления (абсолютный и относительный)



Показа?тель преломле?ния вещества — величина, равная отношению фазовых скоростей света (электромагнитных волн) в вакууме и в данной среде 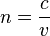
Показатель преломления зависит от свойств вещества и длины волны излучения, для некоторых веществ показатель преломления достаточно сильно меняется при изменении частоты электромагнитных волн от низких частот до оптических и далее, а также может ещё более резко меняться в определённых областях частотной шкалы. По умолчанию обычно имеется в виду оптический диапазон или диапазон, определяемый контекстом.
Существуют оптически анизотропные вещества, в которых показатель преломления зависит от направления и поляризации света. Такие вещества достаточно распространены, в частности, это все кристаллы с достаточно низкой симметрией кристаллической решётки, а также вещества, подвергнутые механической деформации.
Показатель преломления можно выразить как корень из произведения магнитной и диэлектрических проницаемостей среды
(надо при этом учитывать, что значения магнитной проницаемости 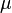

Для измерения показателя преломления используют ручные и автоматические рефрактометры.
Отношение показателя преломления одной среды 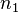
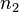
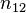
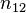
где 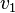
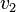
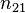
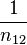
Эта величина, при прочих равных условиях, обычно меньше единицы при переходе луча из среды более плотной в среду менее плотную, и больше единицы при переходе луча из среды менее плотной в среду более плотную (например, из газа или из вакуума в жидкость или твердое тело). Есть исключения из этого правила, и потому принято называть среду оптически более или менее плотной, чем другая (не путать с оптической плотностью как мерой непрозрачности среды).
Луч, падающий из безвоздушного пространства на поверхность какой-нибудь среды, преломляется сильнее, чем при падении на неё из другой среды; показатель преломления луча, падающего на среду из безвоздушного пространства, называется его абсолютным показателем преломления или просто показателем преломления данной среды, это и есть показатель преломления, определение которого дано в начале статьи. Показатель преломления любого газа, в том числе воздуха, при обычных условиях много меньше, чем показатели преломления жидкостей или твердых тел, поэтому приближенно (и со сравнительно неплохой точностью) об абсолютном показателе преломления можно судить по показателю преломления относительно воздуха.
Что такое абсолютный и относительный показатели преломления
Абсолютный показатель преломления вещества равен отношению фазовой скорости света в вакууме к фазовой скорости света в веществе:
Относительным показателем преломления двух сред (второй среды по отношению к первой) называется величина n21, равная отношению абсолютных показателей преломления этих сред:
Было установлено, что показатель преломления не является постоянной величиной, одинаковой для всех длин волн λ, что связано с явлением дисперсии. Дисперсия света как физическое явление – это зависимость фазовой скорости света в среде от частоты ν световой волны или от длины волны λ (или зависимость показателя преломления вещества n от этих же величин).
Зависимость n = n(λ) или n = n(ν) оказывается различной для разных веществ, что учитывают введением термина дисперсия вещества (D), которая характеризует скорость изменения n в зависимости от λ (длина волны света в вакууме):
Дисперсией света объясняется ряд явлений, в числе которых радуга, разноцветный блеск драгоценных камней, разложение белого света на цвета при прохождении через стеклянную призму и т.д.
Явление дисперсии удалось объяснить в рамках электромагнитной теории света и электронной теории вещества.
Элементарная теория дисперсии света.
Максвелл показал, что свет представляет собой электромагнитную волну. Фазовые скорости распространения такой волны в веществе V и в вакууме C различны. Соотношение между ними в соответствии с теорией Максвелла определяется значениями диэлектрической \(\epsilon\) и магнитной \(\mu\) проницаемостей вещества:
Для немагнитных сред можно принять μ = 1. Тогда имеем:
Таким образом, фазовая скорость света в веществе в \(\sqrt<\epsilon>\) раз меньше, чем в вакууме. Учитывая (1), получим:
Из курса «Электричество» известно, что
Для диэлектриков в первом приближении явление поляризации в электрическом поле высокой частоты можно рассматривать как смещение электронов под действием этого поля на некоторое расстояние x относительно положения равновесия в направлении против поля. Ядра атомов при этом можно считать неподвижными, поскольку их масса значительно больше массы электрона. Количественной характеристикой эффекта является поляризованность Р, которая пропорциональна напряжённости электрического поля E:
где ε0 – электрическая постоянная. Равенство (3), с учетом (4), принимает вид:
Выразив из (5) величину æ и подставив ее в последнее равенство, имеем:
Из последнего выражения следует, что экспериментально наблюдаемые различия в значениях показателей преломления для разных веществ и длин волн могут обуславливаться особенностями в поляризации атомов при взаимодействии с электромагнитной волной.
Движение электронов в атоме описывается законами квантовой механики. Однако еще до ее создания Г.Лоренц показал, что для качественного объяснения дисперсии и многих других оптических явлений достаточно ограничится гипотезой о существовании внутри атомов электронов, связанных с атомами квазиупругими силами. Эти силы можно представить в виде:
При прохождении электромагнитной волны через вещество каждый электрон оказывается под действием переменного электрического и магнитного полей. Расчёт показывает, что электрическая сила, действующая на электрон, значительно больше магнитной, так что магнитное поле электромагнитной волны практически не влияет на движение электрона. Напряжённость E электрического поля в электромагнитной волне изменяется по закону:
Поэтому при прохождении через вещество электромагнитной волны на каждый электрон действует также сила
Под действием данной силы электрон совершает вынужденные колебания. В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные с ядром электроны – оптические электроны. Для простоты рассмотрим колебания только одного оптического электрона. Пренебрежем для упрощения затуханием колебаний электрона. Затухание происходит по двум причинам. Во-первых, при ускоренном движении электрона излучаются электромагнитные волны. Во-вторых, имеет место диссипация энергии электромагнитного поля, т.е. превращение ее в другие формы (в теплоту) в результате взаимодействия с другими атомами и соударений. Пренебрегая затуханием, на основании второго закона Ньютона имеем:
Разделив на m и учитывая, что K/m = ω02, получим:
Уравнение (8) описывает вынужденные колебания электрона под действием переменного электрического поля световой волны. Решение этого уравнения имеет вид:
Из последнего равенства видно, что вынужденные колебания электронов происходят с частотой ω, равной частоте колебаний напряженности электрического поля световой волны. Величина
имеет размерность длины и представляет собой амплитуду вынужденных колебаний, которая зависит от ω. Как будет видно из последующего рассмотрения, именно зависимость амплитуды вынужденных колебаний от ω и является причиной дисперсии.
Для одного aтома величина электрического дипольного момента, индуцируемого в результате вынужденных колебаний, составляет:
а дипольный момент, индуцируемый в единице объёма вещества, содержащей N атомов, будет равен
Выражение (9) представляет собой поляризованность вещества. Подставляя выражения (9) и (7) в (6), получаем:
Из (10) видно, что показатель преломления n зависит от ω. Согласно (10), при частотах электромагнитной волны ω ›› ω0 (далёких от резонансной) n2≈1. Зависимость n2 от ω, соответствующая уравнению (10), показана на рис.5 пунктирными кривыми.
Учитывая, что ω=2πC / λ и
находим, что на участках АВ и CD (рис.6), где dn/dλ 0, относится к области аномальной дисперсии.
Как отмечалось, при совпадении ω с ω0 (т.е. при резонансе) резко возрастает амплитуда колебаний электрона. Интенсивно колеблющийся электрон вызывает усиление колебаний атома или увеличение скорости поступательного движения, что приводит к нагреванию вещества. Это является дополнительной причиной затухания колебаний электрона. Таким образом, в области резонанса имеет место явление сильного поглощения, т.е. переход энергии световой волны во внутреннюю энергию вещества. Такое поглощение называется резонансным.
Электроны, входящие в состав атома или молекулы, имеют не одну, а несколько собственных (резонансных) частот колебаний (ω01,ω02,…). Учитывая это, зависимость n2 от ω изменяется. На рис.7 представлена данная зависимость для случая трех резонансных частот. Из рис.6 и 7, следует, что вдали от резонансных частот наблюдается нормальный закон дисперсии, а вблизи этих частот имеет место аномальная дисперсия. Формула (10) с учетом наличия нескольких резонансных частот преобразуется к виду:
Зависимость n2 от ω для случая трёх резонансных частот
Сказанное выше относится к электронам внешних оболочек атомов (оптическим электронам). Именно они взаимодействуют с излучением оптического диапазона. Электроны внутренних оболочек имеют очень высокие собственные частоты, и поле световой волны на них практически не влияет. Данные электроны эффективно взаимодействуют с ультрафиолетовым или рентгеновским излучением.
Определение показателя преломления веществ по углу наименьшего отклонения
Рассмотрим метод определения показателя преломления, применимый для прозрачных веществ. Метод состоит в измерении угла отклонения лучей при прохождении света через призму, изготовленную из исследуемого материала. На призму направляется параллельный пучок лучей, поэтому достаточно рассмотреть ход одного из них (S1) в плоскости, перпендикулярной линии пересечения преломляющих граней призмы (рис.8).
Ход луча через призму рассчитывается на основании законов преломления света. При преломлении на первой грани призмы АС получим
где n – показатель преломления материала призмы для данной длины волны света.
Для грани АВ закон преломления запишется как
Соотношения 12 и 13 позволяют найти выражения для определения n. Однако экспериментально определить углы r1 и i1 достаточно сложно. На практике удобнее измерить угол отклонения луча призмой δ и преломляющий угол призмы φ.
Получим формулу для определения показателя преломления n через углы δ и φ.
Сначала воспользуемся известной в геометрии теоремой, что внешний угол треугольника равен сумме внутренних углов, не смежных с ним. Тогда из треугольника EDF получим
Из треугольника EHF и, используя (14), получим:
Зависимость δ от r1 имеет минимум, условие которого можно найти, приравняв производную δ от r1 нулю:
поэтому r1 = i2. Тогда из законов преломления (12) и (13) следует, что углы i1, r2 также должны быть равны: i1=r2. Принимая во внимание (14) и (15), получим:
C учетом этих равенств окончательно получим:
Следовательно, при наименьшем угле отклонения луча призмой δmin показатель преломления вещества призмы может быть определен по формуле
Таким образом, определение показателя преломления вещества сводится к измерению преломляющего угла призмы и угла наименьшего отклонения лучей.
Экспериментальное определение угла наименьшего отклонения лучей призмой
Сняв призму со столика, наводим зрительную трубу на коллиматор и совмещаем изображение его щели с перекрестием зрительной трубы. Снимаем по лимбу отсчёт S1, соответствующий направлению неотклонённого луча (положение зрительной трубы при этом показано на рис.9 штриховой линией).
Затем призма из исследуемого материала устанавливается на предметном столике гониометра и на одну из её граней направляется параллельный пучок света коллиматора. Источником света служит ртутная лампа, излучение которой состоит из ряда узких спектральных линий. Свет от ртутной лампы поступает на щель коллиматора по гибкому световоду. Благодаря зависимости показателя преломления от длины волны, излучение ртутной лампы, пройдя через призму, разлагается на монохроматические составляющие, идущие под различными углами к первоначальному направлению.
Наблюдая в зрительную трубу и медленно поворачивая её, находим спектральные линии в поле зрения окуляра. Затем поворачиваем предметный столик с призмой так, чтобы спектральные линии приближались к направлению неотклонённого луча и добиваемся такого положения призмы, п+dwри котором угол отклонения лучей от первоначального (S1) направления будет минимальным.
Отсчёты по лимбу, соответствующие каждой спектральной линии обозначим S2.
Величина угла наименьшего отклонения каждой линии спектра находится как разность между двумя отсчётами:
Эксперимент
Оборудование
гониометра, преломляющая призма
Измерение преломляющего угла призмы
Преломляющий угол призмы измеряется на гониометре автоколлимационным методом. Для этого, как показано на рис.10, зрительная труба поочередно устанавливается перпендикулярно граням преломляющего угла призмы. Но на практике более удобно зафиксировать в некотором положении зрительную трубу, а поворачивать предметный столик с призмой так, чтобы нужная грань призмы оказалась перпендикулярной к оси зрительной трубы. Перпендикулярность контролируется по совмещению перекрестия окуляра с изображением автоколлимационного креста, идущего из автоколлиматора и отражающегося от грани призмы. По формуле (18) находим преломляющий угол призмы:
где А1, A2 – отсчёты по лимбу для двух положений зрительной трубы.
Устройство гониометра
Гониометр состоит из массивного основания 24 (см. рис.11) с вертикальной колонкой 28, коллиматором 3 и осевым устройством с алидадой 19, на которой расположена зрительная труба 14. Последнюю вместе с алидадой можно вращать вокруг вертикальной оси прибора вручную или микрометрическим винтом 15 (после закрепления алидады зажимным винтом 23).
Зрительная труба и коллиматор имеют внутреннюю фокусировку, осуществляемую с помощью маховичков 4,13 и одинаковые объективы 16,17. Для регистрации положения установок объективов на бесконечность и величины расфокусировок, трубы снабжены фокусировочными отсчётными шкалами 5,12. Наклон коллиматора и зрительной трубы к горизонтальной оси изменяется юстировочными винтами 6 и 11 соответственно.
На верхней части вертикальной оси гониометра установлен предметный столик 8 (верхняя часть), свободно вращающийся вручную, а после скрепления с нижней частью зажимным винтом 31, он может вращаться вместе с лимбом относительно алидады.
Винтом 29 столик прижимается к центральной неподвижной оси прибора и тогда поворот его в небольших пределах осуществляется микрометренным винтом 30.
С помощью двух винтов 9 столик приводится в горизонтальное положение.
Стеклянный лимб посажен на вертикальную ось прибора и фрикционно соединен с нижней частью столика. Лимб имеет шкалу с ценой деления 20′, оцифрованный через каждый градус от 0°до 359°.
Лимб можно повернуть относительно алидады и столика нажимным маховичком 21.
Шкалу лимба можно наблюдать через окуляр отсчетного устройства 17 при включенном освещении прибора (выключатель 25). Резкость изображения шкалы регулируется вращением оправы окуляра 17.
Оптическая схема отсчетного устройства собрана так, что через окуляр можно наблюдать изображение штрихов двух диаметрально противоположных участков лимба, причём одно изображение прямое, а другое обратное (рис.12). Кроме того, оптическая схема позволяет перемещать эти изображения друг относительно друга, оставляя в покое, как лимб, так и алидаду со зрительной трубой. Это перемещение измеряется при помощи оптического микрометра, цена деления шкалы которого равна 1».
При нажатии рычажка 27 происходит соединение алидады со столиком (и лимбом). В этом случае при вращении алидады шкала лимба в окуляре остается неподвижной. Отключается механизм сцепки нажатием кнопки 26. (В данной работе этот режим не используется).
Снятие отсчета на гониометре.
Отсчет направлений, определяемых гониометром, производится с помощью отсчетного устройства 17, расположенного ниже зрительной трубы. Оптическая схема отсчетного устройства собрана так, что через его окуляр можно наблюдать шкалу лимба, связанного с поворотом зрительной трубы (или нижней частью предметного столика). Шкала подсвечивается лампочкой, включаемой тумблером 25, расположенном в нижней части основания прибора. Резкость изображения шкалы регулируется вращением оправы окуляра отсчетного устройства 17.
Поле зрения отсчетного устройства приведено на Рис.13 и представляет собой два окна.
В левом (большом) окне наблюдаются изображения диаметрально противоположных участков лимба с делениями в виде двойных штрихов (биштрихов) и отсчетный вертикальный индекс. Это окно служит для отсчета градусов и десятков минут.
В правом (маленьком) окне видны деления шкалы оптического микрометра и горизонтальный индекс (линия). Оно служит для отсчета единиц минут (левая часть шкалы) и секунд (правая часть шкалы).
Перед снятием отсчета необходимо совместить верхнюю и нижнюю шкалы по бишрихам с помощью маховика 20 (рис.11-12).
Число градусов (по верхней шкале) будет равно ближайшему числу слева от вертикального индекса (в данном случае 37о).
Число десятков минут равно числу интервалов, заключённых между биштрихом, соответствующим найденному числу градусов, и биштрихом перевернутого числа на нижней шкале, которое оканчивается на такую же цифру, как и найденное число градусов. На рисунке это 37° и перевернутое 217° (эти числа всегда отличаются на 180°). (4 интервала, т.е. 4 десятка).
Число единиц минут отсчитывается по шкале правого окошка по левому вертикальному ряду цифр. Если цифры разные, выбирается та, которая находится выше неподвижной горизонтальной линии (3′).
Число секунд отсчитывается в том же окне по правому ряду чисел относительно горизонтальной линии (52″).
Положение, показанное на рис. 13, соответствует отсчёту 37°43’52».
Порядок выполнения
Подготовка гониометра к работе
Порядок выполнения измерений и вычислений
Измерение угла неотклоненного луча
Измерение углов наименьшего отклонения лучей
Таблица 1
| Линяя | λ,нм | S2 | S1 | A1 | A2 | \(\phi\) |
|---|---|---|---|---|---|---|
| синяя | ||||||
| голубая | ||||||
| зеленая | ||||||
| жёлтая 1 | ||||||
| желтая 2 | ||||||
| желто-ор. | ||||||
| красная |
Определение преломляющего угла призмы
Оформление результатов работы
Для расчетов используйте компьютер.
Таблица соответствия символов
Основные дисперсионные характеристики оптических стекол
В качестве номинальных установлены:
Показатель преломления ne на длине волны λe = 546.07 нм зелёной линии спектра ртути.
Оптические характеристики некоторых марок стекла приведены в таблице Приложения 1.