Чем определяется тип модели при моделировании

Моделирование. Типы моделей.

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемых явлений и факторов передается в форме конкретных математических уравнений.

Моделирование в научных исследованиях используется практически в любых отраслях национального хозяйства, как эффективный инструмент познания того или иного явления или процесса.

Различают по форме представления модели систем: физические, математические, логические, иконографические и др.

Физические модели представляют собой некоторые реальные системы, в которых реализуются те или иные взаимодействия, а также части изучаемого объекта. Физические модели могут быть полными, частичными и аналоговыми.

Полные модели представляют собой реальный объект, выполненный в измененном масштабе с возможностью выполнять полностью или частично функции реального объекта. Так, например, при изучении эффективности очистки воды, строится опытная очистная станция, ее конструкция выполняется в реальном масштабе. Для изучения отдельных частей этой станции могут быть созданы частичные модели, например система обеззараживания воды.

Полные и частичные модели строятся на принципе подобия.

Аналоговые модели строятся на известных аналогиях протекания тех или иных процессов в гидравлике, электротехнике и т.д., с помощью которых можно изучить некоторые экологические процессы в исследуемых системах, например, с помощью создания электрической схемы и ее изучения, полу­ченные результаты можно перенести на экологические систе­мы.

Логические модели реальных систем и процессов представ­ляют собой описания типа «если-то. «, «если «А, то и В. «, «если А и В, то G» и т.д. Логические модели используются в основном для описания тех процессов, которые определяются качественными параметрами.

Иконографические модели реальных систем представляют собой рисунки, схемы, графики и т.п., поясняющие устройст­во, принцип действия или наглядность тех или иных парамет­ров экологических систем и т.п.

Чаще всего в экологических исследованиях применяются смешанные модели, например, логико-математические и др.

Модели систем имеют целевое назначение, например, для исследования структуры, функционирования, расхода и т.д.

Модели структуры предназначены для изучения взаимопо­ложения и связи элементов системы, как внутри ее, так и с внешней средой. Такие модели могут быть представлены в виде схем, сетевых графиков, матриц связи и т.п.

Модели функционирования предназначены для изучения систем в динамике. Так, модели изменения воздушной среды в течение определенного времени; модели операций при изуче­нии технологических процессов и т.д. Характерным призна­ком таких моделей, в большинстве случаев, является измене­ние параметров системы в функции от времени.

Модели расхода или прибыли используются при определе­нии технико-экономических или иных показателей систем, оптимизации процессов по отдельным критериям и т.д.

При изучении экологических процессов и явлений матема­тические модели рассматриваются в тесной связи с целевыми системами и представляют из себя некоторые целостные структуры, которые называют эколого-математическими мо­делями.

Эколого-математические модели представляют из себя смешанные модели (логико-математические, математико-иконографические и т.д.), представляющие определенную со­вокупность математических зависимостей, логических по­строений, схем, матриц и т.д., связанных в некоторую единую систему, имеющую экологический смысл.

Однако, какие бы модели объектов мы не строили, в конце концов, мы должны их сравнивать с реальными объектами, что чаще всего возможно в процессе проведения эксперимента (натурного испытания). В экологии здесь мы сразу же встречаемся со значительными трудностями, так как ее харак­теризуют в основном процессы, имеющие значительную про­должительность во времени и большие трудности воспроиз­водства эксперимента. Поэтому главным направлением в мо­делировании экологических процессов является информаци­онное моделирование, создание изоморфных (каждому эле­менту структуры объекта соответствует один элемент структу­ры модели) абстрактных имитационных моделей, построен­ных на математическом и логическом аппарате и реализуемых на ЭВМ.

По характеру учета времени модели разделяются на динамические, где процесс рассматривается во времени; статические, где состояние процесса изучается в фикси­рованный момент времени, и кинемати­ческие, где течение процесса во времени рассматривается при упрощающих допу­щениях. Наибольшую сложность пред­ставляет построение и изучение динами­ческих процессов.

По форме математического описания модели делятся на две большие группы: стохастические,учитывающие случайные процессы, и детерминированные,в которых элементы случайности не учитываются.

Стохастические модели значительно сложнее детерминированных. По форме их описаний различают модели динамики средних, вероятностные (дискретные и не­прерывные) и статистические.

Источник

Моделирование. Типы моделей

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемых явлений и факторов передается в форме конкретных математических уравнений.

Моделирование в научных исследованиях используется практически в любых отраслях национального хозяйства, как эффективный инструмент познания того или иного явления или процесса.

Различают по форме представления модели систем: физические, математические, логические, иконографические и др.

Физические модели представляют собой некоторые реальные системы, в которых реализуются те или иные взаимодействия, а также части изучаемого объекта. Физические модели могут быть полными, частичными и аналоговыми.

Полные модели представляют собой реальный объект, выполненный в измененном масштабе с возможностью выполнять полностью или частично функции реального объекта. Так, например, при изучении эффективности очистки воды, строится опытная очистная станция, ее конструкция выполняется в реальном масштабе. Для изучения отдельных частей этой станции могут быть созданы частичные модели, например система обеззараживания воды.

Полные и частичные модели строятся на принципе подобия.

Аналоговые модели строятся на известных аналогиях протекания тех или иных процессов в гидравлике, электротехнике и т.д., с помощью которых можно изучить некоторые экологические процессы в исследуемых системах, например, с помощью создания электрической схемы и ее изучения, полу­ченные результаты можно перенести на экологические систе­мы.

Логические модели реальных систем и процессов представ­ляют собой описания типа «если-то. «, «если «А, то и В. «, «если А и В, то G» и т.д. Логические модели используются в основном для описания тех процессов, которые определяются качественными параметрами.

Иконографические модели реальных систем представляют собой рисунки, схемы, графики и т.п., поясняющие устройст­во, принцип действия или наглядность тех или иных парамет­ров экологических систем и т.п.

Чаще всего в экологических исследованиях применяются смешанные модели, например, логико-математические и др.

Модели систем имеют целевое назначение, например, для исследования структуры, функционирования, расхода и т.д.

Модели структуры предназначены для изучения взаимопо­ложения и связи элементов системы, как внутри ее, так и с внешней средой. Такие модели могут быть представлены в виде схем, сетевых графиков, матриц связи и т.п.

Модели функционирования предназначены для изучения систем в динамике. Так, модели изменения воздушной среды в течение определенного времени; модели операций при изуче­нии технологических процессов и т.д. Характерным призна­ком таких моделей, в большинстве случаев, является измене­ние параметров системы в функции от времени.

Модели расхода или прибыли используются при определе­нии технико-экономических или иных показателей систем, оптимизации процессов по отдельным критериям и т.д.

При изучении экологических процессов и явлений матема­тические модели рассматриваются в тесной связи с целевыми системами и представляют из себя некоторые целостные структуры, которые называют эколого-математическими мо­делями.

Эколого-математические модели представляют из себя смешанные модели (логико-математические, математико-иконографические и т.д.), представляющие определенную со­вокупность математических зависимостей, логических по­строений, схем, матриц и т.д., связанных в некоторую единую систему, имеющую экологический смысл.

Однако, какие бы модели объектов мы не строили, в конце концов, мы должны их сравнивать с реальными объектами, что чаще всего возможно в процессе проведения эксперимента (натурного испытания). В экологии здесь мы сразу же встречаемся со значительными трудностями, так как ее харак­теризуют в основном процессы, имеющие значительную про­должительность во времени и большие трудности воспроиз­водства эксперимента. Поэтому главным направлением в мо­делировании экологических процессов является информаци­онное моделирование, создание изоморфных (каждому эле­менту структуры объекта соответствует один элемент структу­ры модели) абстрактных имитационных моделей, построен­ных на математическом и логическом аппарате и реализуемых на ЭВМ.

По характеру учета времени модели разделяются на динамические, где процесс рассматривается во времени; статические, где состояние процесса изучается в фикси­рованный момент времени, и кинемати­ческие, где течение процесса во времени рассматривается при упрощающих допу­щениях. Наибольшую сложность пред­ставляет построение и изучение динами­ческих процессов.

По форме математического описания модели делятся на две большие группы: стохастические,учитывающие случайные процессы, и детерминированные,в которых элементы случайности не учитываются.

Стохастические модели значительно сложнее детерминированных. По форме их описаний различают модели динамики средних, вероятностные (дискретные и не­прерывные) и статистические.

Источник

МЕТОДЫ МОДЕЛИРОВАНИЯ И ТИПЫ МОДЕЛЕЙ

Современные научные исследования во многих сферах человеческой деятельности довольно часто выполняются на основе различных методов и средств моделирования.

Моделирование — это метод познания, исследования объ­ектов и систем путем построения и изучения их моделей.

Все многообразие методов моделирования можно услов­но разделить на две группы: аналитическое и имитацион­ное моделирование.

Аналитическое моделирование заключается в построе­нии модели, основанной на описании свойств или операто­ра F₀объекта в виде аналитических выражений — формул. При таком моделировании объект описывается системой линейных или нелинейных алгебраических или дифферен­циальных уравнений, решение которых аналитическими или приближенными численными методами может дать представление о свойствах объекта. Реализация числен­ных методов обычно возлагается на вычислительные ма­шины. Применение аналитического моделирования огра­ничено сложностью получения и анализа выражений для больших систем.

Имитационное моделирование предполагает построе­ние модели объекта с неизвестными свойствами на основе информации о его входных и выходных переменных. Воз­действия, поступающие на вход модели и объекта, долж­ны вызывать одинаковые изменения выходов модели иобъекта. Изменяя входные переменные и получая измене­ния выходных переменных, можно проанализировать ха­рактеристики объекта.

Модель (от лат. modulus — образец) — это некий аналог, заменитель оригинала, отражающий существенные харак­теристики исследуемого объекта, явления или процесса.

Заменяя объект моделью, на ней можно провести необ­ходимые исследования за минимальное время и без каких-либо потерь.

Если результаты моделирования подтверждаются ре­альными данными и могут служить основой для прогнози­рования поведения исследуемых объектов, то говорят, что модель адекватна объекту. Степень адекватности зависит от цели и критериев моделирования.

Все модели можно разбить на два класса: материаль­ные и информационные.

Материальные модели воспроизводят геометрические, физические, химические и другие свойства объектов в ма­териальной форме (глобус, тренажер и др.).

Информационная модель — это описание объекта в об­разной или знаковой форме.

Образные информационные модели (рисунки, схемы, фотографии и др.) представляют собой зрительные образы объектов, нанесенные на какой-либо носитель информа­ции (бумага, фото- и кинопленка и др.). Образные инфор­мационные модели широко используются в образовании — это учебные плакаты по различным дисциплинам.

Знаковые информационные модели строятся с исполь­зованием различных языков (знаковых систем). Знаковы­ми информационными моделями являются тексты (напри­мер, программа на языке программирования), формулы (например, второй закон Ньютона f = mа), таблицы (на­пример, периодическая таблица элементов Д. И. Менде­леева) и т. д.

Информационные модели, описывающие объект на ес­тественном языке, называются вербальными. Например, различного рода инструкции — это вербальные информа­ционные модели поведения человека в тех или иных си­туациях.

Опишем кратко другие типы информационных моделей.

Табличная информационная модель, или просто пря­моугольная таблица, состоящая из строк и столбцов, при­меняется для описания объектов, обладающих одинако­выми наборами свойств.

Иерархическая информационная модель характеризу­ется распределением объектов по уровням. На первом уров­не может находиться только один объект. Объект нижнего уровня может быть связан только с одним объектом более высокого уровня.

Сетевая информационная модель применяется для описания систем со сложной структурой, в которой связи между объектами носят произвольный характер.

Определим понятия формализации и формальных язы­ков, используемые при построении формальных информа­ционных моделей.

Формализацией называется процесс построения инфор­мационных моделей с привлечением формальных языков.

К формальным языкам относятся: естественные язы­ки, языки программирования и разделы математики: диф­ференциальное и интегральное исчисление, теория мно­жеств, алгебра логики и т. д.

Математическая модель представляет собой совокуп­ность математических формул и логических выражений.

Источник

Понятие модели и моделирования

Сам по себе процесс моделирования в полной мере не формализован, большая роль в этом принадлежит опыту инженера. Но, тем не менее, рассматриваемый в теме процесс создания модели в виде шести этапов может стать основой для начинающих и с накоплением опыта может быть индивидуализирован.

1.1. Общее определение модели

Однако во многих случаях натурный эксперимент невозможен.

Например, наиболее полную оценку новому виду вооружения и способам его применения может дать война. Но не будет ли это слишком поздно?

Натурный эксперимент с новой конструкцией самолета может вызвать гибель экипажа.

Натурное исследование нового лекарства опасно для жизни человека.

Натурный эксперимент с элементами космических станций также может вызвать гибель людей.

Время подготовки натурного эксперимента и проведение мероприятий по обеспечению безопасности часто значительно превосходят время самого эксперимента. Многие испытания, близкие к граничным условиям, могут протекать настолько бурно, что возможны аварии и разрушения части или всего объекта.

Из сказанного следует, что натурный эксперимент необходим, но в то же время невозможен либо нецелесообразен.

Выход из этого противоречия есть и называется он » моделирование «.

Моделирование, в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу. Чтобы такой перенос был оправдан, между моделью и оригиналом должно быть сходство, подобие.

Остановимся на основных целях моделирования.

Часто модель создается для применения в качестве средства обучения: модели-тренажеры, стенды, учения, деловые игры и т. п.

Гениальный полководец А. В. Суворов перед атакой крепости Измаил тренировал солдат на модели измаильской крепостной стены, построенной специально в тылу.

Наш знаменитый механик-самоучка И. П. Кулибин (1735-1818) создал модель одноарочного деревянного моста через р. Неву, а также ряд металлических моделей мостов. Они были полностью технически обоснованы и получили высокую оценку российскими академиками Л. Эйлером и Д. Бернулли. К сожалению, ни один из этих мостов не был построен.

1.2. Классификация моделей и моделирования

Каждая модель создается для конкретной цели и, следовательно, уникальна. Однако наличие общих черт позволяет сгруппировать все их многообразие в отдельные классы, что облегчает их разработку и изучение. В теории рассматривается много признаков классификации, и их количество не установилось. Тем не менее, наиболее актуальны следующие признаки классификации:

1.2.1. Классификация моделей и моделирования по признаку «характер моделируемой стороны объекта»

В соответствии с этим признаком модели могут быть:

Функциональные модели отображают только поведение, функцию моделируемого объекта. В этом случае моделируемый объект рассматривается как «черный ящик», имеющий входы и выходы. Физическая сущность объекта, природа протекающих в нем процессов, структура объекта остаются вне внимания исследователя, хотя бы потому, что неизвестны. При функциональном моделировании эксперимент состоит в наблюдении за выходом моделируемого объекта при искусственном или естественном изменении входных воздействий. По этим данным и строится модель поведения в виде некоторой математической функции.

1.2.2. Классификация моделей и моделирования по признаку «характер процессов, протекающих в объекте»

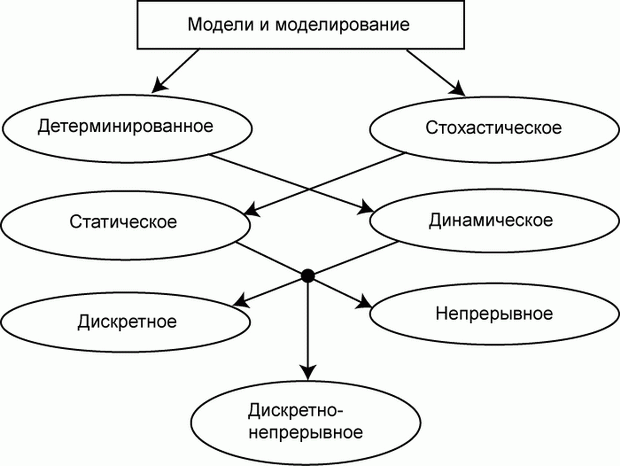
По этому признаку модели могут быть детерминированными или стохастическими, статическими или динамическими, дискретными или непрерывными или дискретно-непрерывными.

Детерминированные модели отображают процессы, в которых отсутствуют случайные воздействия.

Стохастические модели отображают вероятностные процессы и события.

Статические модели служат для описания состояния объекта в какой-либо момент времени.

Динамические модели отображают поведение объекта во времени.

Дискретные модели отображают поведение систем с дискретными состояниями.

Непрерывные модели представляют системы с непрерывными процессами.

Дискретно-непрерывные модели строятся тогда, когда исследователя интересуют оба эти типа процессов.

Очевидно, конкретная модель может быть стохастической, статической, дискретной или какой-либо другой, в соответствии со связями, показанными на рис. 1.1.

Источник

Понятие модели и моделирования

1.2.3. Классификация моделей и моделирования по признаку «способ реализации модели»

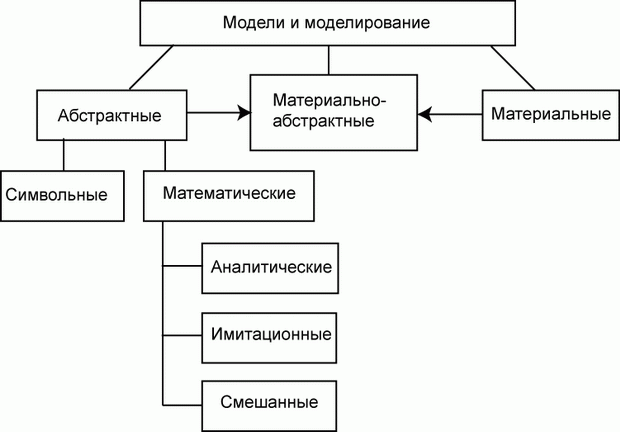
Согласно этому признаку модели делятся на два обширных класса:

Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.

Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.

Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:

Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.

Математические модели могут быть:

Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик («в общем виде»). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.

В чем заключается отличие имитационных и аналитических моделей?

В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.

Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.

Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.

1.3. Этапы моделирования

Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.

Обычно целями моделирования являются:

Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.

В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.

Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.

Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.

На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.

Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.

Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.

Источник