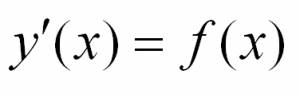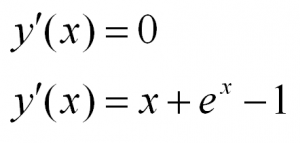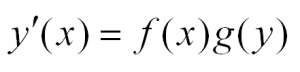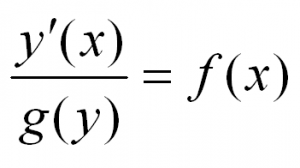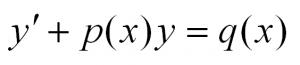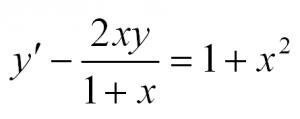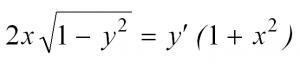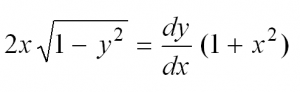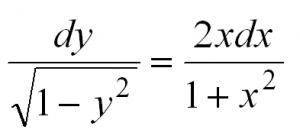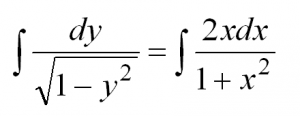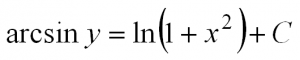Чем определяется порядок дифференциального уравнения

Порядок дифференциального уравнения и его решения, задача Коши

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.

Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.

Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения, связывающие независимые переменные , неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».

Примеры дифференциальных уравнений:

(1) ;

(2) ;

(3) ;

(4) ;

(5) .

Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.

Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.

Процесс нахождения решения дифференциального уравнения называется его интегрированием.

Пример 1. Найти решение дифференциального уравнения .

Решение. Запишем данное уравнение в виде . Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть первообразная для , т. е.

.

Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.

Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.

Решение дифференциального уравнения в примере 1 является общим.

Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.

Пример 2. Найти общее решение дифференциального уравнения и частное решение при .

Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.

,

,

.

данного дифференциального уравнения третьего порядка.

Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим

.

Если кроме дифференциального уравнения задано начальное условие в виде , то такая задача называется задачей Коши. В общее решение уравнения подставляют значения и и находят значение произвольной постоянной C, а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.

Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии .

Решение. Подставим в общее решение значения из начального условия y = 3, x = 1. Получаем

.

Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:

.

При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.

Пример 4. Найти общее решение дифференциального уравнения .

Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.

.

Применяем метод интегрирования заменой переменной (подстановкой). Пусть , тогда .

Возвращаясь к переменной x, получаем:

.

Это и есть общее решение данного дифференциального уравнения первой степени.

Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.

Пример 5. Найти общее решение дифференциального уравнения .

Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального исчисления, что производная может быть записана также в виде . В результате уравнение приобретает вид

,

то есть, в нём в некотором виде появился x.

Теперь вспомнаем одно из свойств пропорции: из пропорции выткают следующие пропорции:

,

то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

Применяя это свойство, преобразуем уравнение к виду

,

после чего интегрируем обе части уравнения:

.

и получаем решение данного дифференциалного уравнения первого порядка:

.

Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.

Источник

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

У одного дифференциального уравнения может быть множество решений.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

К числу основных задач из теории дифференциальных уравнений относятся:

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

Остальные определения мы будем разбирать в других темах по мере изучения теории.

Источник

Дифференциальные уравнения для «чайников». Примеры решения

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

Приведем примеры подобных дифференциальных уравнений:

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

Частные решения мы можем выбрать из систем независимых функций:

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Источник

Как решать дифференциальные уравнения

Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.

Основные понятия и определения

Определения

Типы уравнений

Алгоритм решения

ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.

Алгоритм нахождения общего решения:

После замены производной игрека исходное уравнение приобретает такой формат:

Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Однородные ДУ

Решается по следующему алгоритму:

Интегрируем обе части:

$$\lambda x \cdot \lambda y + (\lambda y)^2 = (2 (\lambda x)^2 + \lambda x\cdot \lambda y)y’$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ$$y^2 = Cxe^\frac<-y>$$

Линейные неоднородные ДУ

Алгоритм метода Бернулли:

Алгоритм метода вариации произвольной постоянной:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

ДУ Бернулли

ДУ в полных дифференциалах

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ$$x^2+5xy+y^3 = C.$$

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:

Линейные однородные ДУ с постоянными коэффицентами

В зависимости от получившихся корней имеем общее решение в различных видах:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ$$y = C_1 e^ <-2x>+ C_2 e^$$

Линейные неоднородные ДУ с постоянными коэффициентами

Ответ$$y = C_1 \cos x + C_2 \sin x + x\cos x + x^2\sin x$$

Метод Лагранжа

Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.

Источник