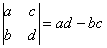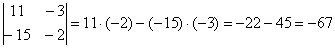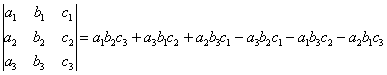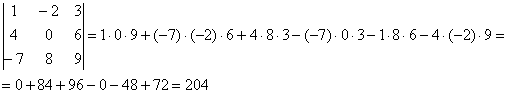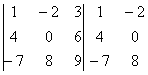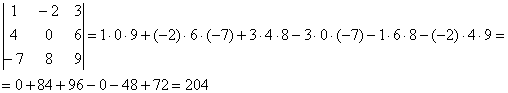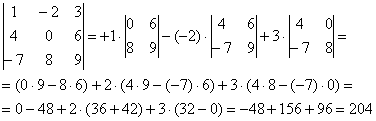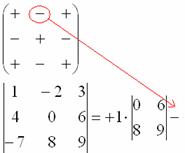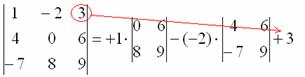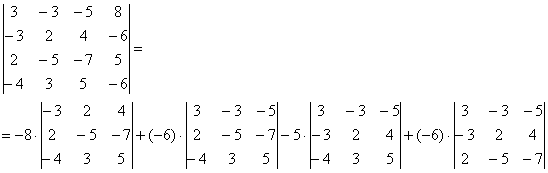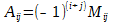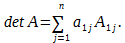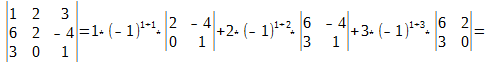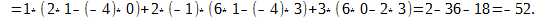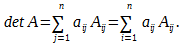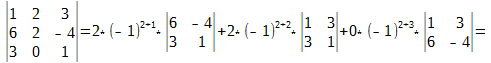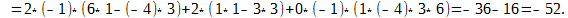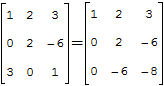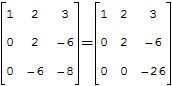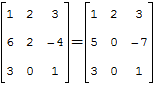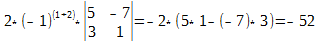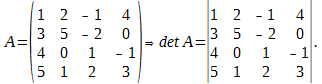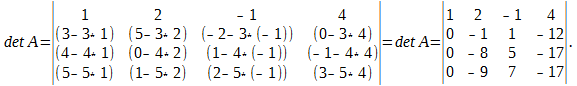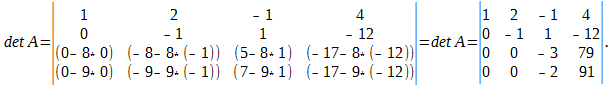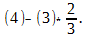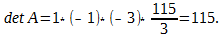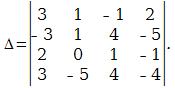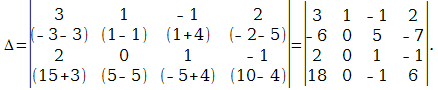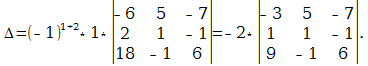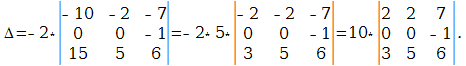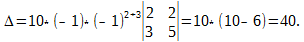Чем определяется порядок детерминантов

Как вычислить определитель?

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)

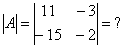
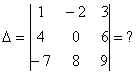
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка 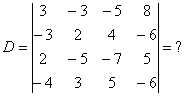тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

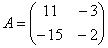
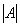
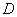
Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса 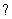в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два»:

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
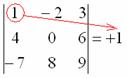
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

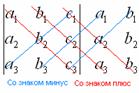
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке.
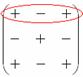
Для этого нам понадобится матрица знаков: 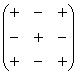. Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот: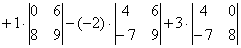
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: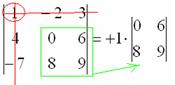

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

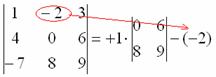
Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: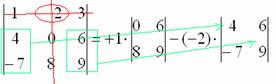

Оставшиеся четыре числа записываем в маленький определитель.

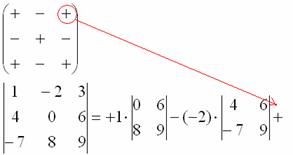
Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент: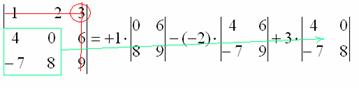

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
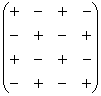
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу:

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

ОПРЕДЕЛИТЕЛЬ

Полезное

Смотреть что такое «ОПРЕДЕЛИТЕЛЬ» в других словарях:

ОПРЕДЕЛИТЕЛЬ — ОПРЕДЕЛИТЕЛЬ, определителя, муж. (книжн.). 1. То, что определяет, выражает собою что нибудь. 2. Книга, служащая для справок при определении чего нибудь (научн.). Определитель растений. Определитель грибов. 3. Выражение, составляемое из… … Толковый словарь Ушакова

ОПРЕДЕЛИТЕЛЬ — (детерминант) составленное по определенному правилу из n2 чисел математическое выражение, применяемое при решении и исследовании систем алгебраических уравнений 1 й степени. Число n называется порядком определителя. Так, определитель 2 го порядка … Большой Энциклопедический словарь

определитель — опознаватель, гессиан, минор, детерминант Словарь русских синонимов. определитель сущ., кол во синонимов: 10 • автоопределитель (1) • … Словарь синонимов

ОПРЕДЕЛИТЕЛЬ — (детерминант) составленное по определённому правилу из n2 чисел математическое выражение, применяемое при решении и исследовании систем алгебраических уравнений 1 й степени. Число п называется порядком определителя. Так, определитель 2 го порядка … Большая политехническая энциклопедия

ОПРЕДЕЛИТЕЛЬ — ОПРЕДЕЛИТЕЛЬ, я, муж. 1. Устройство для определения чего н., а также вообще то, с помощью чего можно что н. точно определить, установить. Телефон с определителем номера. О. ритма. 2. Книга для справок при определении чего н. (спец.). О. растений … Толковый словарь Ожегова

ОПРЕДЕЛИТЕЛЬ — (детерминант) квадратнойматрицы А = ||aij|| порядка n, detA многочлен … Физическая энциклопедия

определитель — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN determinant … Справочник технического переводчика

Определитель — У этого термина существуют и другие значения, см. Определитель (значения). Определитель (или детерминант) одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у … Википедия

определитель — 3.4.6 определитель (auxiliary): Код вспомогательного класса УДК. Источник … Словарь-справочник терминов нормативно-технической документации

определитель — я; м. 1. Книжн. То, чем определяется, обусловливается что л. Звук может быть определителем скорости. Главным определителем времени является движение Солнца в космическом пространстве. 2. Спец. Руководство (книга или таблица) для определения чего… … Энциклопедический словарь

Источник

Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение

Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам:

(можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке).

Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки равны нулю. Пример такой матрицы:

Для неё определитель равен:

Обратите внимание, что

это вычисление детерминанта матрицы, полученой вычетом строки и столбца, на пересечении которых находиться единственное не нулевое числов строки/столбца, по которому мы разлагаем матрицу:

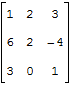
Если привести матрицу к треугольному виду, то её определитель вычисляется как произведение цифр по диагонали. Например, для матрицы

Аналогично следует поступать с матрицами 5×5, 6×6 и другими больших размерностей.

Преобразования матриц нужно выполнять в соответствии со свойствами определителя. Но прежде чем перейти к практике по вычислению определителя для матриц 4×4, давайте вернёмся к матрицам 3×3 и подробно рассмотрим, как вычисляется определитель для них.

Минор

Определитель матрицы не очень прост для понимания, поскольку в его понятии присутствует рекурсия: определитель матрицы состоит из нескольких элементов, в том числе из определителя (других) матриц.

Чтобы не застрять на этом, давайте прямо сейчас (временно) примем, что определитель матрицы

Ещё разберёмся в условных обозначения и в таких понятиях как минор и алгебраическое дополнение.

Буквой i мы обозначаем порядковый номер стоки, буквой j – порядковый номер столбца.

a_ij означает элемент матрицы (цифру) на пересечении строки i и столбца j.

Представим себе матрицу, которая получена из исходной удалением строки i и столбца j. Определитель новой матрицы, которая получена из исходной удалением строки i и столбца j, называется минором M_ij элемента a_ij.

Проиллюстрируем сказанное. Предположим, дана матрица

Тогда для определения минора M₁₁ элемента a₁₁ нам нужно составить новую матрицу, которая получается из исходной удалением первой строки и первого столбца:

И вычислить для неё определитель: 2*1 — (-4)*0 = 2

Для определения минора M₂₂ элемента a₂₂ нам нужно составить новую матрицу, которая получается из исходной удалением второй строки и второго столбца:

Алгебраическое дополнение

Алгебраическим дополнением А_ij для элемента a_ij называется минор M_ij этого элемента, взятый со знаком «+», если сумма индексов строки и столбца (i + j), на пересечении которых стоит этот элемент, чётная, и со знаком «-», если сумма индексов нечётная.

Для матрицы из предыдущего примера

Вычисление определителя для матриц

Определителем порядка n, соответствующим матрице А, называется число, обозначаемое det A и вычисляемое по формуле:

В этой формуле нам всё уже знакомо, давайте теперь посчитаем определитель матрицы для

Каков бы ни был номер строки i=1,2,…, n или столбца j = 1, 2,…, n определитель n-го порядка равен сумме произведений элементов этой строки или этого столбца на их алгебраические дополнения, т. е.

Т.е. детерминант можно вычислить по любому столбцу или по любой строке.

Чтобы убедиться в этом, вычислим определитель для матрицы из последнего примера по второму столбцу

Свойства определителя матриц

Для вычисления определителя любого порядка можно применять метод последовательного понижения порядка определителя. Для этого пользуются правилом разложения определителя по элементам строки или столбца. Еще один способ вычисления определителей заключается в том, чтобы с помощью элементарных преобразований со строками (или столбцами), прежде всего в соответствии со свойствами 4 и 7 определителей, привести определитель к виду, когда под главной диагональю определителя (определяемой так же, как и для квадратных матриц) все элементы равны нулю. Тогда определитель равен произведению элементов, расположенных на главной диагонали.

При вычислении определителя последовательным понижением порядка для уменьшения объема вычислительной работы целесообразно с помощью свойства 7 определителей добиться обнуления части элементов какой-либо строки или какого-либо столбца определителя, что уменьшит число вычисляемых алгебраических дополнений.

Приведение матрицы к треугольному виду, преобразование матрицы, облегчающее вычисление определителя

Показанные ниже методы нецелесообразно использовать для матриц 3×3, но я предлагаю рассмотреть суть методов на простом примере. Воспользуемся матрицей, для которой мы уже считали определитель — нам будет проще проверить правильность вычислений:

Используя 7-е свойство определителя, вычтем из второй строки третью, умноженную на 2:

из третьей строки вычтем соответствующие элементы первой строки определителя, умноженные на 3:

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Как видим, ответ совпал с полученными ранее.

Давайте вспомним формулу определителя матрицы:

Детерминант — это сумма алгебраических дополнений, умноженная на члены одной из строк или одного из столбцов.

Если в результате преобразований мы сделаем так, что одна из строк (или столбец) будет состоять полностью из нулей кроме одной позиции, то нам не нужно будет считать все алгебраические дополнения, поскольку они заведомо будут равны нулю. Как и предыдущий метод, этот целесообразно применять для матриц больших размеров.

Покажем пример на той же самой матрице:

Вычислим определитель по второму столбцу. Нам нужно посчитать только одно алгебраическое дополнение, поскольку остальные заведомо сводятся к нулю:

Вычисление определителя для матриц 4×4, 5×5 и больших размерностей

Чтобы избежать слишком больших вычислений для матриц больших размеров следует делать преобразования, описанные выше. Приведём пару примеров.

Вычислить определитесь матрицы

Р е ш е н и е. Используя 7-е свойство определителя, вычтем из второй строки третью, из четвёртой строки — соответствующие элементы первой строки определителя, умноженные соответственно на 3, 4, 5. Эти действия сокращённо будем обозначать так: (2) — (1) * 3; (3) — (1) * 4; (4) — (1) * 5. Получим:

Далее, в соответствии с ведёнными обозначениями, выполним действия: (3) — (2) * 8; (4) — (2) * 9. Получаем

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Вычислить определитель

Разлагая полученный определитесь по второй строке имеем:

(Затем мы вынесли сомножитель 2 первого столбца на основании свойства 4). Далее прибавим к элементам первого и второго столбца элементы определителя. Получим:

Затем мы вынесли множитель в первом столбце, а затем общий множитель (-1) в первой строке. Разлагая теперь получившийся определитесь третьего порядка по элементам второй строки получим:

Здесь определитесь второго порядка вычислен в соответствии с его определением, по формуле

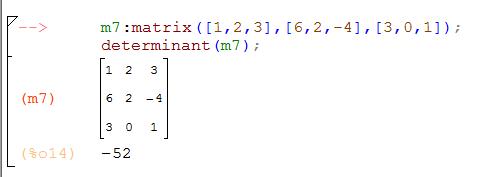
Вычисление определителя (детерминанта) матрицы wxMaxima и Maxima

В wxMaxima и Maxima для вычисления определителя используется функция determinant:

Для приведения матриц к треугольному виду можно воспользоваться функцией triangularize:

Источник