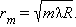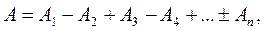Чем определяется порядок интерференционного максимума

Чем определяется порядок интерференционного максимума

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).

Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов (см. § 3.6).

где – амплитуда волны, – волновое число, – длина волны, – круговая частота. В оптических задачах под следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке результирующее колебание также происходит на частоте и имеет некоторую амплитуду и фазу :

Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.

Если в схеме Юнга через обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда и (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:

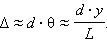Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек.

При то есть в центре (точка соприкосновения) поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум – темное пятно. Радиусы последующих темных колец определяются выражением

Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких – интенсивности волн, т. е. квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.

Источник

Условия интерференционного максимума и минимума

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в одинаковой фазе, и в точке М будет наблюдатьсяинтерференционный максимум(m – порядок интерференционного максимума).

то колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе, и в точке М будет наблюдатьсяинтерференционный минимум(m – порядок интерференционного минимума). В качестве примера наблюдения интерференции световых волнрассмотрим метод Юнга.

Метод Юнга. Для наблюдения интерференции света когерентные световые пучки получают разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экрана и щелей.

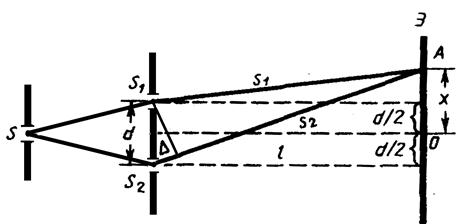
Источником света служит ярко освещенная щель S (рис. 1), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников, а

интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии l от щелей S₁ и S₂ (рис. 1) . Щели S₁ и S₂ находятся на расстоянии d друг от друга (рис. 1), причем l >> d.

Согласно рисунку 1 :

; ,

откуда

или .

.

Согласно этому соотношению и условиям наблюдения интерференционных максимумов и минимумов положения максимумов (x_max) и минимумов (x_min) интенсивности на экране в методе Юнга определяются следующим образом:

Расстояние между двумя соседними максимумами (или минимумами) Dx называется шириной интерференционной полосыи равно:

.

Из этого соотношения следует, что величина Dx зависит от длины световой волны l₀ . Поэтому, четкая интерференционная картина, представляющая собой чередова­ние на экране светлых и темных полос, параллельных друг другу, возможна только при использовании монохроматического света, то есть света определенной длины волны l₀. Если же использовать белый свет, представляющий собой непрерыв­ный набор длин воли от 0,40мкм (фиолетовая граница видимого спектра) до 0,75мкм (красная граница видимого спектра), то интерференционные максимумы для каждой длины волны будут смещены на экране друг относительно друга, и светлые полосы будут иметь вид радужных полос. Только в середине экрана будет наблюдаться белая полоса, так как для всех длин воли в середине экрана выполняются условияинтерференционных максимумов, соответствующих значению m = 0.

Тема 2. Дифракция света. Дифракция Френеля

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятст­вий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д.

Явление дифракции объясняется с помощью принципа Гюйгенса, соглас­но которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта.

Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн.

Согласнопринципу Гюйгенса – Френеля световая волна, возбуждаемая каким-ли­бо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить, например, бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Если в качестве такой замкнутой поверхности выбрать одну из волновых поверх­ностей (волновой поверхностью называется геометрическое место точек, колебания в которых происходят в одинаковой фазе), то все бесконечно малые элементы этой замкнутой поверхности, как фиктивные источники, действуют синфазно. Это свойство фиктивных источников коге­рентных вторичных волн использовано в методе зон Френеля при изучении дифракции сферических волн точечного источника света.

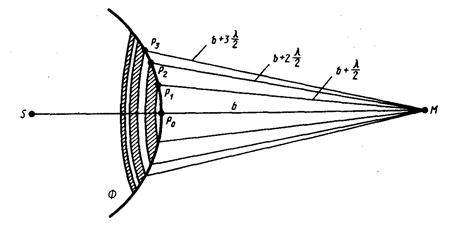
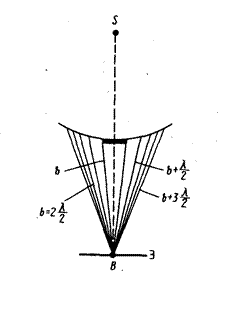
Метод зон Френеля.Найдем в произвольной точке М амплитуду световой волны, распространяющейся от точечного источника света S (рис. 2).

Френель разбил волновую поверхность Ф, являющуюся сферической поверхностью с центром в точке S, на кольцевые зоны (зоны Френеля) такого размера, чтобы расстояния от краев соседних зон до точки М отличались на l/2 (рис. 2). Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположных фазах и при наложении взаимно ослабляют друг друга. Поэтому амплитуда А результирующего колебания в точке М определяется следующим образом:

С ростом номера зоны Френеля интенсивность излучения в направлении точки М уменьшается, то есть .

Амплитуда А результирующего колебания может быть представлена в виде:

так как выражения, стоящие в скобках, близки к нулю, а амплитуда A_n последней n-ной зоны Френеля ничтожно мала.

Таким образом, амплитуда результирующего колебания в произвольной точке М соответствует действию только половины центральной зоны Френеля.

Дифракция Френеля на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием (рис. 3). Дифрак­ционная картина на экране Э зависит от числа зон Френеля, открытых круглым отверстием. После разбиения открытой части волновой поверхности Ф на зоны Френеля, необходимо определить их

Рис. 3 число. Если для точки В, лежащей на линии, соединяющей источник S с центром отверстия (рис. 3), число открытых зон Френеля окажется четным, то в этой точке В будет наблюдаться темное пятно, так как колебания от каждой пары соседних зон Френеля взаимно гасят друг друга. Если же число открытых зон Френеля окажется нечетным, то в точке В будет наблюдаться светлое пятно. Причем для нечетного числа открытых зон Френеля амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны.

Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.4). Пусть для точки В, лежащей на линии, соединяющей источник S с центром диска, после разбиения волновой поверхности Ф на зоны Френеля окажутся закрытыми диском m первых зон Френеля. Тогда амплитуда

Рис. 4 результирующего колебания в точке В равна:

так как выражения, стоящие в скобках, обращаются в нули, а оставшаяся часть от амплитуды последней n-ной зоны ничтожно мала.

Следовательно, в точке В будет наблюдаться светлое пятно, соответствующее действию поло­вины первой открытой зоны Френеля.

Источник

Условия интерференционного максимума и минимума

Тема 9. Волновая теория света. Интерференция света. Метод Юнга

Интерференцией волн называется явление усиления колебаний в одних точках пространства и ослабления колебаний в других точках в результате наложения двух или более волн, приходящих в эти точки. При наложении двух (или нескольких) световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – мини­мумы интенсивности. Необходимым условием наблюдения устойчивой интерференционной картины является когерентность складываемых волн. Когерентными называются волны одинаковой частоты, колебания в которых отличаются постоянной во времени разностью фаз.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и в результате наблюдается интерференци­онная картина.

Произведение геомет­рической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, a величина D = L₂ – L₁ (разность оптических длин проходимых волнами путей) называется оптической разностью хода.

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в одинаковой фазе, и в точке М будет наблюдаться интерференционный максимум (m – порядок интерференционного максимума).

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в противофазе, и в точке М будет наблюдаться интерференционный минимум (m – порядок интерференционного минимума).

В качестве примера интерференции световых волн рассмотрим метод Юнга.

Метод Юнга. Для наблюдения интерференции света когерентные световые пучки получают разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Источником света служит ярко освещенная щель S (рис. 20), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников, а интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии l от щелей S₁ и S₂ (рис. 20) . Щели S₁ и S₂ находятся на расстоянии d друг от друга (рис. 20), причем l >> d.

Интерференция рассматривается в произ­вольной точке А на экране, расположенной на расстоянии x от точки O, симметричной от­носительно щелей и принятой за начало отсчета величины x.

Согласно рисунку 20 :

; , откуда или .

.

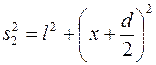
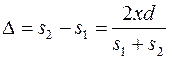
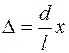
Согласно этому соотношению и условиям наблюдения интерференционных максимумов и минимумов положения максимумов (x_max) и минимумов (x_min) интенсивности на экране в методе Юнга определяются следующим образом:

Расстояние между двумя соседними максимумами (или минимумами) Dx называется шириной интерференционной полосы и равно:

.

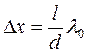
Тема 10. Дифракция света. Дифракция Френеля

Дифракцией называется огибание волнами препятствий. Дифракцию света определяют как любое отклонение распространения света вблизи препятст­вий от законов геометрической оптики. Благодаря дифракции волны попадают в область геометрической тени, проникают через небольшие отверстия и т. д.

Явление дифракции объясняется с помощью принципа Гюйгенса, соглас­но которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта.

Согласно принципу Гюйгенса – Френеля световая волна, возбуждаемая каким-ли­бо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить, например, бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Если в качестве таковой выбрать одну из волновых поверх­ностей (волновой поверхность – это геометрическое место точек, колебания в которых происходят в одинаковой фазе), то все бесконечно малые элементы этой замкнутой поверхности, как фиктивные источники, действуют синфазно. Это свойство фиктивных источников коге­рентных вторичных волн использовано в методе зон Френеля при изучении дифракции сферических волн.Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн.

Метод зон Френеля. Найдем в произвольной точке М амплитуду световой волны, распространяющейся от точечного источника света S (рис. 21).

Френель разбил волновую поверхность Ф, являющуюся сферической поверхностью с центром в точке S, на кольцевые зоны (зоны Френеля) такого размера, чтобы расстояния от краев соседних зон до точки М отличались на l/2 (рис. 21). Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противофазе и при наложении взаимно ослабляют друг друга. Поэтому амплитуда А результирующего колебания в точке М:

В результате сложения амплитуда А результирующего светового колебания в точке М оказалась равной половине амплитуды А₁ центральной зоны Френеля:

. То есть, амплитуда светового колебания, идущего только от одной центральной зоны Френеля вдвое больше, чем амплитуда результирующего светового колебания при полностью открытом волновом фронте. Этот эффект подтвержден экс­периментально с помощью зонных пластинок, на практике, стеклянных пластинок, построенных по методу зон Френеля. Зонные пластинки состоят из чередующихся прозрачных (для нечетных зон Френеля) и непрозрачных (для четных зон Френеля) концентрических колец. В этом случае результирующая амплитуда А (A=A₁+A₃+A₅+. ) больше, чем при полностью открытом волновом фронте. Опыт подтвердил, что зонные пластинки увеличивают освещенность в точке М, действуя подобно собирающей линзе.

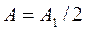
Дифракция Френеля на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути круглое отверстие (рис. 22). Дифрак­ционная картина на экране зависит от числа зон Френеля, открытых круглым отверстием. После разбиения открытой части волновой поверхности Ф на зоны Френеля для точки В, лежащей на экране (рис. 22), определяют число открытых зон. Если число открытых зон Френеля четное, то в точке В наблюдается темное пятно, так как колебания от каждой пары соседних зон Френеля взаимно гасят друг друга. Если же число открытых зон Френеля нечетное, то в точке В будет светлое пятно.

Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис. 23). Пусть для точки В, лежащей на линии, соединяющей источник S с центром диска, после разбиения волновой поверхности Ф на зоны Френеля окажутся закрытыми диском m первых зон Френеля. Тогда амплитуда А результирующего колебания в точке В равна: 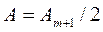, то есть в точке В будет светлое пятно, соответствующее действию поло­вины первой открытой зоны Френеля.

Источник

Интерференция волн.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

Сложение колебаний.

Опыт показывает, что волны складываются друг с другом в следующем смысле.

Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.

Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).

Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.

Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.

Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!

Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1 ).

Рис. 1. Волны в фазе: усиление колебаний

Рис. 2. Волны в противофазе: гашение колебаний

Когерентные источники.

Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.

Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.

Условие максимума и минимума.

Рис. 3. Усиление колебаний в точке P

Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.

Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:

Рис. 4. Гашение колебаний в точке P

Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:

Равенство (2) можно переписать следующим образом:

Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.

Интерференционная картина.

А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.

Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.

Теперь, наконец, мы можем сказать, что такое интерференция.

Интерференция — это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.

Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.

Рис. 5. Интерференция волн двух точечных источников

Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.

Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.

В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.

На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.

Рис. 6. Интерференционная картина на экране

Рис. 7. Вычисление координат максимумов

Раз так, можно использовать приближённую формулу:

Точно так же вычисляем расстояние, которое проходит волна от источника до точки наблюдения:

Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):

Источник