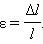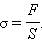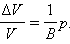Чем определяется коэффициент деформации

Сопротивление материалов. Шпаргалка для студентов

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов предоставлен нашим книжным партнёром — компанией ЛитРес.

5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации

Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот — длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения — поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε’ — деформации, приходящиеся на единицу длины или пощади сечения стержня.

где Δl — изменение длины стержня;

Δa — изменение площади сечения.

Продольную деформацию растяжения обычно считают положительной, деформацию сжатия — отрицательной. Продольная и поперечная деформации связаны соотношением

μ — коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.

В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.

Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости — это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.

Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:

Произведение EA называется жесткостью сечения.

При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.

Источник

коэффициент деформации

Полезное

Смотреть что такое «коэффициент деформации» в других словарях:

коэффициент уширения — [spread ratio] показатель деформации, равный отношению ширины полосы после деформации к ее ширине до деформации; Смотри также: Коэффициент фабрикационный коэффициент температурный … Энциклопедический словарь по металлургии

коэффициент Пуассона — [Poisson s ratio] упругая константа материала, равная отношению относительной поперечной деформации (ε2 и ε3) к относительной продольной деформации (ε1) при линейном растяжении или сжатии: μ = ε2/ε1 = ε3/ε1 = const. Коэффициент Пуассона разных… … Энциклопедический словарь по металлургии

коэффициент обжатия — [reduction ratio] один из показателей деформации, выражающий отношение высоты или толщины материала до деформации к высоте и толщине его после деформирования; Смотри также: Коэффициент фабрикационный коэффициент температурный … Энциклопедический словарь по металлургии

коэффициент вытяжки — [drawing ratio; extrusion ratio] 1. Показатель деформации, равный отношению длины материала после деформирования к его длине до деформирования или отношение площади поперечного сечения материала до и после деформирования; обычно обозначается λ… … Энциклопедический словарь по металлургии

коэффициент упрочнения — [strengthening coefficient] отношение напряжения текучести металла (σт) после окончательного деформирования к напряжению текучести металла в момент начала процесса; зависит от степени и скорости деформации; Смотри также: Коэффициент… … Энциклопедический словарь по металлургии

коэффициент овальности — [ovality factor] показатель овализации гильзы при поперечно винтовой прокатке, выражающий отношение расстояния между линейками к расстоянию между рабочими валками в данном сечении очага деформации; Смотри также: Коэффициент фабрикационный… … Энциклопедический словарь по металлургии

коэффициент нормальной пластической анизотропии — [plastic strain ratio] показатель способности материала к глубокой вытяжке, выраженным отношением логарифмической деформации по ширине и толщине листового образца при испытаниях на растяжение. Смотри также: Коэффициент фабрикационный коэффициент … Энциклопедический словарь по металлургии

коэффициент Лоде-Надаи — [Lode Nadai coefficient] коэффициент, примемененный В. Лоде и А. Падай для выражения величины среднего главного напряжения через величины двух крайних главных напряжений: σ2 = 0,5(σ1 + σ3) + μ(σ1 σ3). Обозначение μ или к и записанного в виде μ =… … Энциклопедический словарь по металлургии

коэффициент асимметрии цикла — [cycle ratio] отношение минальных значений деформации напряжения, коэффициента интенсивности напряжений и т. п. к максимальному при циклическом нагружении; Смотри также: Коэффициент фабрикационный коэффициент температурный … Энциклопедический словарь по металлургии

коэффициент эффективности — [efficiency factor] относительный качественный показатель, характеризующий достигнутый уровень экономической эффективности; отношение экономического результата (например, суммы прибыли или экономии от снижения себестоимости продукции и т. п.).… … Энциклопедический словарь по металлургии

Источник

Коэффициент поперечной деформации

Коэффициент поперечной деформации

равна ДД Сжатие стержня продольной деформации представляет собой укороченное, скрещенное растяжение. Эксперименты показывают, что для большинства материалов 3-4E в 3 раза меньше, чем.§ 9] коэффициент поперечной деформации 39

Абсолютное значение отношения относительной поперечной деформации (et) Людмила Фирмаль

к относительной продольной деформации (e) называется коэффициентом поперечной деформации или коэффициентом Пуассона (l: Р= Людмила Фирмаль

……………. М е д ы……………….. Б р о н з а…………….. Железо………………. Вести. ……………. Бюстгальтеры……………. Алюминиевый………. С и н К……………….. 0.25-0.33 0.31-0.34 0.32-0.35 0.23-0.27 0.45 0,32-0,42 0.32-0.36 0.21 Золото……………. Серебро…………. Стекло……………. Камни……………. Б е т о н………………. Резинка……………. Штекер……………. Фанера……………. Целлулоид. ……… 0.42 0.39 0.25 0.16-0.34 0.08-0.18 0.47 0.00 0.07 0.39 Зная это, можно рассчитать изменение объема образца при растяжении или сжатии. Длина образца после деформации равна Z(1—| — e). Площадь после деформации равна f(1-EP.4. Объем после деформации С=Ч(1 4-й) (1_fxs)’=в(1+е) (1-СЕ)’где V-первоначальный объем. E-это небольшое количество до предела пропорциональности, поэтому мы игнорируем этот квадрат. Тогда объем C равен V1=y[l+e (l-

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Чем определяется коэффициент деформации

В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.

Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.

Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.

Отношение абсолютного удлинения к первоначальной длине образца называется относительным удлинением или относительной деформацией :

Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то при деформации растяжения и – при сжатии. Отношение модуля внешней силы к площади сечения тела называется механическим напряжением :

За единицу механического напряжения в СИ принят паскаль (). Механическое напряжение измеряется в единицах давления.

Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).

На рис. 3.7.1 (3) показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением в жидкости. Относительная деформация определяется как отношение изменения объема к первоначальному объему тела. При малых деформациях

Величина модуля всестороннего сжатия определяет скорость звука в данном веществе (см. §2.7).

Источник

Сила упругости

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

Сила упругости: Закон Гука

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, про­порциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Закон Гука

Fупр = kx

Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

Тогда из Закона Гука выразим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

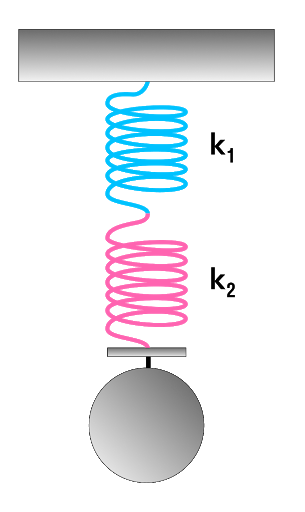
Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

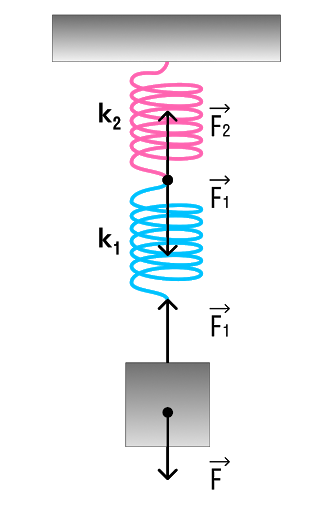
Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k_i

k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

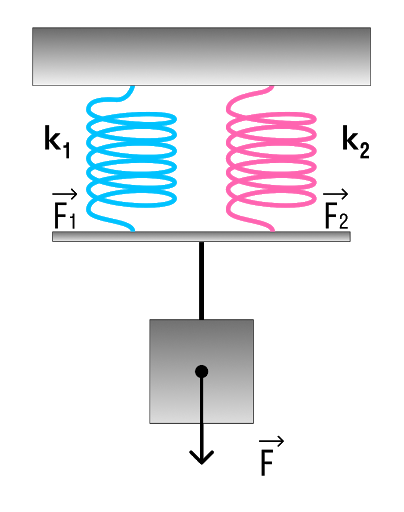
Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

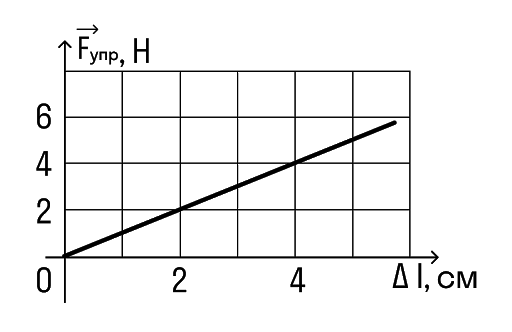
Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

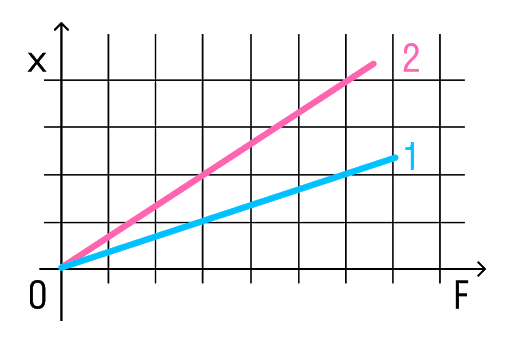
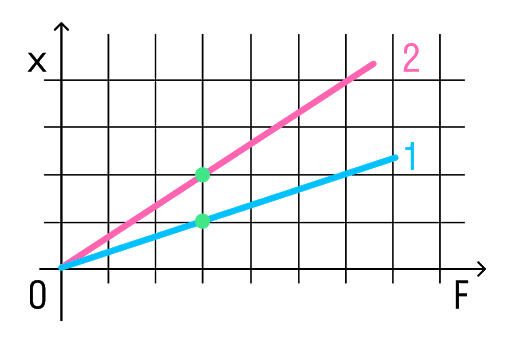
Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.