Что значит угол при вершине

Внешний угол треугольника

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

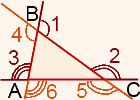
∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано : ∆АВС, ∠1 — внешний угол при вершине С.

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Источник

Определение и формулы для вычисления элементов треугольника

Одной из самых изученных фигур в математике является треугольник. Вычисление его элементов выполняется по формулам, полученным благодаря открытию свойств геометрического тела. Изучают их в седьмом классе средней школы. Эти знания позже используются для доказательства ряда теорем и нахождения параметров более сложных фигур.

Общие сведения

Ещё в Древней Греции появилась довольно полная теория геометрии треугольников. Их свойствами в своё время занимались: Евклид, Архимед, Птолемей, Папп Александрийский. Весомый вклад в развитие науки внесли индийские учёные. Именно они к концу XIII века открыли и доказали базовые теоремы, после успешно используемые на практике. Но только через четыре века благодаря трудам Лейбница, Торричелли, Эйлера были обнаружены замечательные линии и точки фигуры.

Под треугольником в математике понимают ломанную замкнутую линию, на которой можно выделить три отрезка, соединяющих такое же количество точек, не лежащих на одной прямой. По сути, треугольная фигура является частным случаем многоугольника, обладающего тремя углами. Точки соприкосновения отрезков называют вершинами, а прямые, образующие их — сторонами. Плоскость, заключённая внутрь фигуры, является внутренней. Она фактически образует площадь треугольника. Вершины фигуры принято обозначать с помощью заглавных букв. С их помощью подписывают и сам треугольник, например, ABC. Часто в обозначение добавляют значок Δ. Сторону обычно подписывают тем же символом, что и вершину противолежащего угла, но при этом используют прописные буквы. Существуют несколько классификаций треугольников. Чаще всего применяют разделение по числу равных сторон. Согласно ему, фигуры с тремя углами бывают:

В равнобедренном треугольнике равные отрезки называю боковыми, а отличную от них сторону — основанием. Так как из определения рассматриваемый многоугольник имеет три угла, то существует классификация и по их величине. Когда они у фигуры острые, то её называют остроугольной, один из них прямой — прямоугольным, а если тупой — тупоугольным.

Вершины, углы и стороны

Как и любое геометрическое тело, треугольник состоит из элементов. С их помощью классифицируют многоугольник, а также определяют его основные параметры. Например, вычисляют площадь или периметр, находят длины различных отрезков. Зная основные величины, можно выполнить сравнение фигур, доказать их равенство или подобие. К основным частям, из которых состоит многоугольник, относят вершины, стороны, углы.

Изучают способы нахождения элементов треугольника в 7 классе средней школы. Для решения задачи должны быть известны некоторые данные. Так, существует пять возможных вариантов, позволяющих вычислить основные элементы фигуры. Их можно перечислить в следующей последовательности:

К основным методам, позволяющим выполнять вычисления, относят теоремы синусов и косинусов. Согласно одной из них, квадрат стороны треугольника равен сумме квадратов двух оставшихся отрезков минус их удвоенное произведение, умноженное на косинус противолежащего ей угла: a 2 = b 2 + c 2 — 2* b * c * cos (a). Это правило справедливо для нахождения любой стороны: b 2 = a 2 + c 2 — 2* a * c * cos (b), c 2 = a 2 + b 2 — 2* a * b * cos (с). Теорема синусов позволяет составить отношение вида: a / sin (a) = b / sib (b) = c / sin (с). То есть её определение звучит так: противолежащие углы обратно пропорциональны сторонам треугольника. Существует расширенная версия правила. Согласно ему, такое отношение равняется диаметру вписанной в фигуру окружности. Но чаще используют не его, а удвоенное произведение радиуса: a / sin (a) = 2 * R.

На практике кроме основных правил применяют теоремы тангенсов и котангенсов, метод проекций и формулы Мольвейде. Первые две являются следствием из утверждений о синусах и косинусах. Формулировка первой утверждает, что верным является следующее равенство: (a — b) / (a + b) = tg ((a — b) / 2) / tg ((a + b) / 2). Второй же связывает радиус вписанной окружности с величиной сторон: ctg (a) / 2 = p — BC / r, где: BC — длина стороны, a — не принадлежащий ей угол, p — полупериметр, r — радиус вписанной окружности. Теорема о проекциях используется при решениях, связанных с остроугольными фигурами. Записывают её в следующем виде: b = c * cos (a) + a * cos (b). Формулы Мольвейде выражают тригонометрические соответствия при вершинах треугольника. Они имеют вид: (a + b) / c = cos ((a — b) / 2) / sin (с / 2); (a — b) / c = sin ((a — b) / 2) / cos (с / 2). Причём если разделить отдельно правые и левые части, то получится теорема тангенсов.

Второстепенные части

К дополнительным элементам, которые можно выделить в треугольнике, относят и так называемые замечательные линии. Своё имя они получили из-за тех или иных интересных свойств. Кроме этого, в треугольном многоугольнике выделяют несколько видов точек. Их особенность: вне зависимости от того, в каком порядке используются стороны и вершины фигуры, местоположение точек однозначно определяется треугольником. К особым прямым фигуры относят:

К замечательным точкам относят место пересечения медиан, биссектрис и высоты. В любой фигуре ортоцентр, центр тяжести и описанной окружности располагаются на одной прямой. Её принято называть Эйлеровской, по имени математика.

Решение задач

Знание значений перечисленных элементов позволяет вычислять различные параметры фигуры, например углы, площадь, стороны, без выполнения измерений. Этим довольно часто и пользуются на практике. Но для успешного решения геометрических задач необходимо не только знать элементы, но и уметь вычислять площадь фигуры (S = a * h / 2) и периметр (P = a + b + c). Вот некоторые из типовых заданий, рассчитанных на группу учеников среднего уровня подготовки:

Следует отметить, что в частных случаях для вычисления размеров элементов треугольника можно использовать упрощённые формулы.

Одной из самых изученных фигур в математике является треугольник. Вычисление его элементов выполняется по формулам, полученным благодаря открытию свойств геометрического тела. Изучают их в седьмом классе средней школы. Эти знания позже используются для доказательства ряда теорем и нахождения параметров более сложных фигур.

Общие сведения

Ещё в Древней Греции появилась довольно полная теория геометрии треугольников. Их свойствами в своё время занимались: Евклид, Архимед, Птолемей, Папп Александрийский. Весомый вклад в развитие науки внесли индийские учёные. Именно они к концу XIII века открыли и доказали базовые теоремы, после успешно используемые на практике. Но только через четыре века благодаря трудам Лейбница, Торричелли, Эйлера были обнаружены замечательные линии и точки фигуры.

Под треугольником в математике понимают ломанную замкнутую линию, на которой можно выделить три отрезка, соединяющих такое же количество точек, не лежащих на одной прямой. По сути, треугольная фигура является частным случаем многоугольника, обладающего тремя углами. Точки соприкосновения отрезков называют вершинами, а прямые, образующие их — сторонами. Плоскость, заключённая внутрь фигуры, является внутренней. Она фактически образует площадь треугольника. Вершины фигуры принято обозначать с помощью заглавных букв. С их помощью подписывают и сам треугольник, например, ABC. Часто в обозначение добавляют значок Δ. Сторону обычно подписывают тем же символом, что и вершину противолежащего угла, но при этом используют прописные буквы. Существуют несколько классификаций треугольников. Чаще всего применяют разделение по числу равных сторон. Согласно ему, фигуры с тремя углами бывают:

В равнобедренном треугольнике равные отрезки называю боковыми, а отличную от них сторону — основанием. Так как из определения рассматриваемый многоугольник имеет три угла, то существует классификация и по их величине. Когда они у фигуры острые, то её называют остроугольной, один из них прямой — прямоугольным, а если тупой — тупоугольным.

Вершины, углы и стороны

Как и любое геометрическое тело, треугольник состоит из элементов. С их помощью классифицируют многоугольник, а также определяют его основные параметры. Например, вычисляют площадь или периметр, находят длины различных отрезков. Зная основные величины, можно выполнить сравнение фигур, доказать их равенство или подобие. К основным частям, из которых состоит многоугольник, относят вершины, стороны, углы.

Изучают способы нахождения элементов треугольника в 7 классе средней школы. Для решения задачи должны быть известны некоторые данные. Так, существует пять возможных вариантов, позволяющих вычислить основные элементы фигуры. Их можно перечислить в следующей последовательности:

К основным методам, позволяющим выполнять вычисления, относят теоремы синусов и косинусов. Согласно одной из них, квадрат стороны треугольника равен сумме квадратов двух оставшихся отрезков минус их удвоенное произведение, умноженное на косинус противолежащего ей угла: a 2 = b 2 + c 2 — 2* b * c * cos (a). Это правило справедливо для нахождения любой стороны: b 2 = a 2 + c 2 — 2* a * c * cos (b), c 2 = a 2 + b 2 — 2* a * b * cos (с). Теорема синусов позволяет составить отношение вида: a / sin (a) = b / sib (b) = c / sin (с). То есть её определение звучит так: противолежащие углы обратно пропорциональны сторонам треугольника. Существует расширенная версия правила. Согласно ему, такое отношение равняется диаметру вписанной в фигуру окружности. Но чаще используют не его, а удвоенное произведение радиуса: a / sin (a) = 2 * R.

На практике кроме основных правил применяют теоремы тангенсов и котангенсов, метод проекций и формулы Мольвейде. Первые две являются следствием из утверждений о синусах и косинусах. Формулировка первой утверждает, что верным является следующее равенство: (a — b) / (a + b) = tg ((a — b) / 2) / tg ((a + b) / 2). Второй же связывает радиус вписанной окружности с величиной сторон: ctg (a) / 2 = p — BC / r, где: BC — длина стороны, a — не принадлежащий ей угол, p — полупериметр, r — радиус вписанной окружности. Теорема о проекциях используется при решениях, связанных с остроугольными фигурами. Записывают её в следующем виде: b = c * cos (a) + a * cos (b). Формулы Мольвейде выражают тригонометрические соответствия при вершинах треугольника. Они имеют вид: (a + b) / c = cos ((a — b) / 2) / sin (с / 2); (a — b) / c = sin ((a — b) / 2) / cos (с / 2). Причём если разделить отдельно правые и левые части, то получится теорема тангенсов.

Второстепенные части

К дополнительным элементам, которые можно выделить в треугольнике, относят и так называемые замечательные линии. Своё имя они получили из-за тех или иных интересных свойств. Кроме этого, в треугольном многоугольнике выделяют несколько видов точек. Их особенность: вне зависимости от того, в каком порядке используются стороны и вершины фигуры, местоположение точек однозначно определяется треугольником. К особым прямым фигуры относят:

К замечательным точкам относят место пересечения медиан, биссектрис и высоты. В любой фигуре ортоцентр, центр тяжести и описанной окружности располагаются на одной прямой. Её принято называть Эйлеровской, по имени математика.

Решение задач

Знание значений перечисленных элементов позволяет вычислять различные параметры фигуры, например углы, площадь, стороны, без выполнения измерений. Этим довольно часто и пользуются на практике. Но для успешного решения геометрических задач необходимо не только знать элементы, но и уметь вычислять площадь фигуры (S = a * h / 2) и периметр (P = a + b + c). Вот некоторые из типовых заданий, рассчитанных на группу учеников среднего уровня подготовки:

Следует отметить, что в частных случаях для вычисления размеров элементов треугольника можно использовать упрощённые формулы.

Источник

Треугольник

Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников

По величине углов

Остроугольный треугольник

— все углы треугольника острые.

Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).

По числу равных сторон

Разносторонний треугольник

— все три стороны не равны.

Равнобедренный треугольник

Равносторонний (правильный) треугольник

— все три стороны равны.

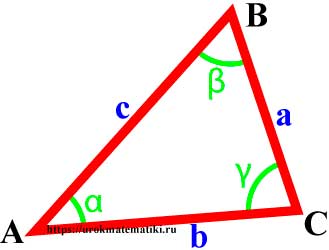
Вершины, углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

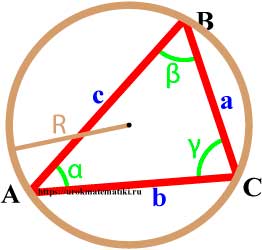
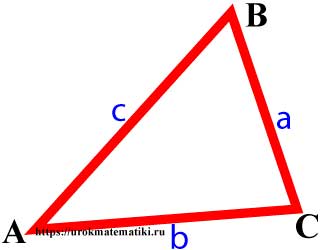
Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

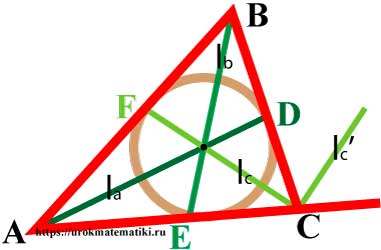
Медианы треугольника

Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Формулы медиан треугольника

Формулы медиан треугольника через стороны

Биссектрисы треугольника

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника

Угол между l c и l c ‘ = 90°

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

где p = a + b + c 2 — полупериметр треугольника.

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

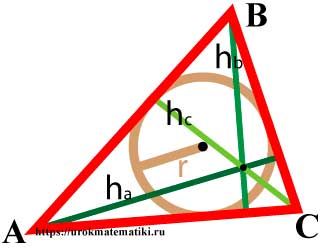
Высоты треугольника

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться:

Свойства высот треугольника

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

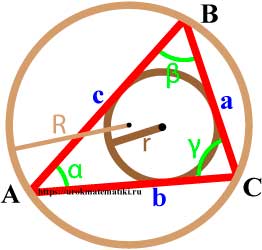
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

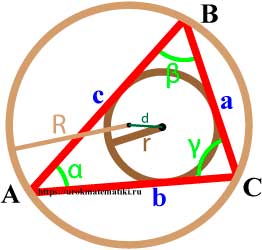
Связь между вписанной и описанной окружностями треугольника

Формулы радиуса окружности описанной вокруг треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то

Радиус описанной окружности через площадь и три угла

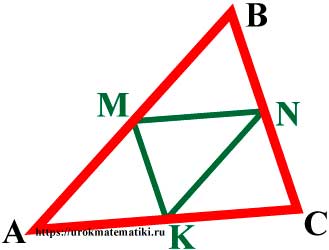
Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

Признаки

Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a, b, c — стороны треугольника,
h_a, h_b, h_c — высоты, проведенные к сторонам a, b, c треугольника.

Формула площади треугольника по трем сторонам

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

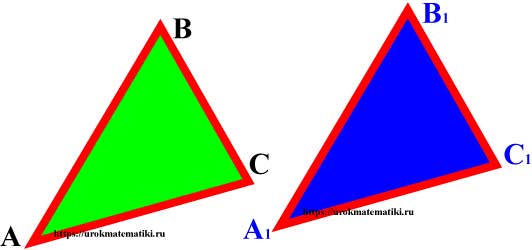
Равенство треугольников

Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

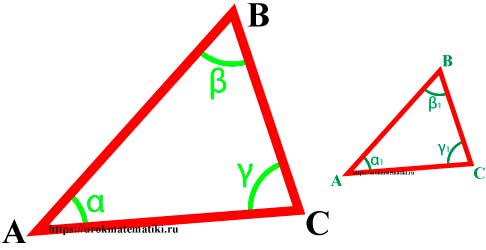
Подобие треугольников

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

где k — коэффициент подобия.

Признаки подобия треугольников

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Прямоугольные треугольники

Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).

Свойства прямоугольного треугольника

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Источник