Что значит цифра снизу
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 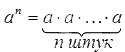
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Свойства степеней. Действия со степенями
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).
Числа. Степень числа.
То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».
Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.
В общем виде степень с основанием «a» и показателем «n» записывается так
Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а
Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1
Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a
Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.
-при нахождении степени положительного числа получается положительное число.
-при вычислениях нуля в натуральной степени получаем ноль.
— при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.
Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.
Свойства степени с натуральным показателем.
Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:
Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:
При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.
например: (2 3 ) 2 = 2 3·2 = 2 6
Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель
При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби
Последовательность выполнения расчетов при работе с выражениями содержащими степень.
При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.
Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.
Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.
Тайны «кода паспорта»: что означают цифры в документе
Что означают цифры под фотографией в паспорте нового образца — это основные данные владельца документа: его Ф. И. О., дата рождения и гражданство.
Что означают буквы и цифры под фотографией
С 1 июля 2011 года в бланке российского паспорта появилась дополнительная запись — на третьей странице, в нижней ее четверти, непосредственно под фотографией. Это машиночитаемая запись. Догадаться, что написано в паспорте в строчках мелким шрифтом, несложно — это основные сведения документа, изложенные по специально разработанным правилам кодирования информации.
Расшифровка того, что означают цифры под фотографией в паспорте нового образца, изложена в приказе МВД №773 от 16.11.2020.
Машиночитаемая запись под фото содержит две строки.
Используйте бесплатный доступ к инструкциям от экспертов КонсультантПлюс, чтобы:
Верхняя строка содержит следующую информацию:
Вторая строка содержит преимущественно цифры:
Аналогичен ответ на вопрос, что означают последние 2 цифры в паспорте внизу после галочки, — это кодовые числа, первое из которых шифрует последний информационный блок в строке, а второе — всю нижнюю строку. Они, как и предшествующие им три контрольных числа, введены для дополнительной защиты от подделок.
Удостоверение личности гражданина РФ — это документ, обладающий несколькими степенями защиты и множеством разнообразных защитных элементов, кодов и секретов. Например, мало кто замечает, что строки на третьей странице — это не сплошные линии, они состоят из очень мелких букв.
Ответ на вопрос, что за загадочные микроскопические слова вместо строчек в паспортах РФ на удивление прост: это повторяющееся название соответствующей строки. Например, строка «Отчество» выглядит как «отчествоотчествоотчество», а «Пол» — «полполполполпол».
На фото приближенные строчки из букв в паспорте выглядят так:
Как расшифровать серию и номер
Помимо машиночитаемого кода под фото, удостоверение содержит и широко применяемые реквизиты — серию и номер. Ответ на вопрос, как расшифровывается серия паспорта РФ, следующий:
Номер удостоверения не кодирует какой-либо информации — это порядковый номер бланка. В некоторых странах номер паспорта должен быть буквенно-цифровым, в России он только цифровой, содержит шесть знаков без пробелов.
При использовании такой системы формирования серии и номера документа получается, что в каждом регионе страны ежегодно есть возможность выдать 999 999 удостоверений, и во всей стране не найдется двух с одинаковыми реквизитами.
Как и весь номер документа, последние 5 цифр паспорта не сообщают какой-либо информации о владельце, а только обозначают порядковый номер бланка в серии.
Цифры в паспорте. Как расшифровываются запись под фотографией, серия и номер документа
— В паспортах под фотографией есть два ряда цифр и надписей. Фамилия, имя и отчество — это понятно, а что значит остальное?
— Россияне получают паспорта с новыми строками на третьей странице еще с 2011 года. В самом низу, прямо под фото, есть машиночитаемая запись. В ней содержатся зашифрованные специальным кодом сведения о владельце и документе. Расскажем, что значат две строки с буквами и символами, а также вспомним, что обозначают цифры в номере и серии паспорта.
❗ Обозначение цифр в паспорте под фотографией
Что значит набор цифр в бланках паспорта – подробно расшифровали в Приложении №24 Приказа МВД №773 от 16 ноября 2020 года. Здесь указан алгоритм формирования машиночитаемой записи, и расписана полная структура данных обеих строк.
Машиночитаемая запись на третьей странице паспорта состоит из двух строк по 44 символа в каждой. Данные верхней строки — это преимущественно фамилия, имя и отчество (если оно есть). Эти данные закодированы способом «модернизированный клер», в котором буквы кириллицы обозначаются латинскими буквами и арабскими цифрами (например, Ё — это 2, а Й — Q). В нижней строке цифровым способом закодированы другие сведения о гражданине и о документе.
Верхняя строка
В верхней строке слева направо зашифрованы:
Нижняя строка
В нижней строке закодированы следующие сведения:
✅ Серия и номер паспорта
Серия и номер паспорта тоже «скрывают» некоторую информацию:

