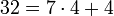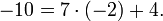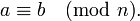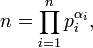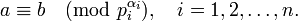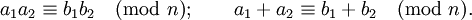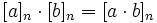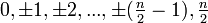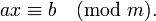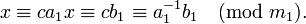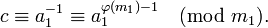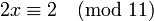Что значит сравнить числа по модулю
Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
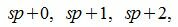 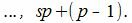 |
Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
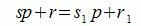 |
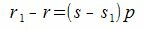 | (2) |
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
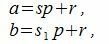 |
где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
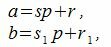 |
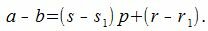 |
По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
При делении все обстоит иначе. Из сравнения
не всегда следует сравнение
Утверждение 5. Пусть
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
Так как m(a−b) делится на k, то
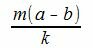 |
имеет нулевой остаток. Тогда
 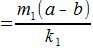 . . |
 |
имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
и m является один из делителей числа p, то
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
Сравнение по модулю натурального числа
Сравнение по модулю натурального числа
В теории чисел сравнение [уточнить] по модулю натурального числа n — задаваемое означенным числом отношение эквивалентности на множестве целых чисел, связанное с делимостью на него. Факторпространство по этому отношению называется «кольцом вычетов». Совокупность соответствующих тождеств и алгоритмов образует модульную [уточнить] (или модулярную) арифметику.
Содержание
Определения
Два целых числа a и b сравнимы по модулю натурального числа n (или равноостаточны при делении на n ), если при делении на n они дают одинаковые остатки.
Утверждение « a и b сравнимы по модулю n » записывается в виде:
Свойства равенства по модулю
Отношение сравнения по модулю обладает свойствами
Любые два целых числа a и b сравнимы по модулю 1.
Для того, чтобы числа a и b были сравнимы по модулю n, необходимо и достаточно, чтобы их разность делилась на n.
Если числа 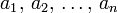
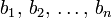
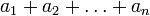
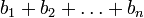
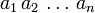
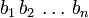
Если числа a и b сравнимы по модулю n, то их степени a k и b k тоже сравнимы по модулю n при любом натуральном k.
Если числа a и b сравнимы по модулю n, и n делится на m, то a и b сравнимы по модулю m.
Для того, чтобы числа a и b были сравнимы по модулю n, представленному в виде его канонического разложения на простые сомножители pi
необходимо и достаточно, чтобы
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 
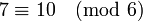
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
Связанные определения
Классы вычетов
Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел 
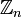
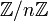
Операции сложения и умножения на 
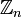
[a]n + [b]n = [a + b]n
Относительно этих операций множество 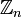
Системы вычетов
Система вычетов позволяет осуществлять арифметические операции над конечным набором чисел, не выходя за его пределы. Полная система вычетов по модулю n ― любой набор из n несравнимых между собой по модулю n целых чисел. Обычно в качестве полной системы вычетов по модулю n берутся наименьшие неотрицательные вычеты
или абсолютно наименьшие вычеты, состоящие из чисел
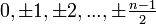
в случае нечётного n и чисел
Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Пример
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: 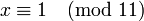
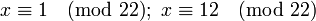
Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
Китайская теорема об остатках, известная уже много столетий, утверждает (на современном математическом языке), что кольцо вычетов по модулю произведения нескольких взаимно простых чисел является прямым произведением соответственных множителям колец вычетов.
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Модуль числа, сравнение чисел
Вы будете перенаправлены на Автор24
Модуль числа
Данное определение модуля числа можно записать следующим образом:
Можно использовать более краткую запись:
Модуль числа является абсолютной величиной числа.
Таким образом, модуль числа – число под знаком модуля без учета его знака.
Модуль числа как расстояние
Геометрическое значение модуля числа: модуль числа – это расстояние.
Готовые работы на аналогичную тему
Модуль числа как арифметический квадратный корень
Сравнение отрицательных чисел
Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.
Правило сравнения отрицательных чисел:
На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа.
При сравнении отрицательных рациональных чисел необходимо преобразовать оба числа к виду обыкновенных дробей или десятичных дробей.
Сравнение чисел с противоположными знаками
Правило сравнения чисел с противоположными знаками:
Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.
По данному правилу можно сравнивать также и действительные числа с противоположными знаками.
Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 06 2021
Что значит сравнить числа по модулю
ВНИМАНИЕ! В связи с новой волной пандемии и шумом вокруг вакцинации агрессивные антивакцинаторы банятся без предупреждения, а их особенно мракобесные комментарии — скрываются.
Основные условия публикации
— Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
— Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
— Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
— Видеоматериалы должны иметь описание.
— Названия должны отражать суть исследования.
— Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
Не принимаются к публикации
— Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
— Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
— Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
— Оскорбления, выраженные лично пользователю или категории пользователей.
— Попытки использовать сообщество для рекламы.
— Многократные попытки публикации материалов, не удовлетворяющих правилам.
— Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает @SupportComunity и общество пикабу.
Решение сравнений по модулю
Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m
Решение сравнений по модулю
Решений нет
Сравнение по модулю
Сравнение двух целых чисел по модулю натурального числа m — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на m один и тот же остаток. Арифметические операции с остатками чисел по одному и тому же модулю образуют модулярную арифметику.
Сравнимость чисел a и b по модулю сравнения m записывается как
называется сравнением первой степени или линейным сравнением по модулю m.
Для проверки существования решений сравнения сначала вычисляется НОД(a, m). Если b не кратно полученному НОД, то у сравнения нет решений.
Если кратно, то количество решений по модулю m равно полученному НОД.
Существует несколько алгоритмов нахождения всех решений сравнения, но в данном калькуляторе применяется алгоритм решения линейных диофантовых уравнений с двумя переменными. В самом деле, сравнение эквивалентно следующему линейному диофантовому уравнению:
поэтому я использовал уже реализованный калькулятор решения линейных диофантовых уравнений для получения общей формулы решения, после чего выбрал все частные решения в диапазоне от 0 до m.