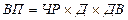Что значит создать детерминированную факторную систему
Экономический анализ хозяйственной деятельности. Ответы на экзаменационные билеты
Книга содержит материал, касающийся таких вопросов экономического анализа, как понятие, роль, задачи, виды, предмет, объект, принципы экономического анализа, планирование, способы и методы аналитической работы. Написанное простым, доступным языком пособие станет помощником студентам при подготовке к экзаменам и людям, интересующимся экономическим анализом хозяйственной деятельности.
Оглавление
Приведённый ознакомительный фрагмент книги Экономический анализ хозяйственной деятельности. Ответы на экзаменационные билеты предоставлен нашим книжным партнёром — компанией ЛитРес.
7. Систематизация факторов. Моделирование взаимосвязей в факторном анализе
Системный подход в экономическом анализе хозяйственной деятельности вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и соподчиненности, что достигается с помощью систематизации.
Систематизация — это размещение изучаемых явлений или объектов в определенном порядке с выявлением их взаимосвязи и соподчиненности.
Виды факторных систем:
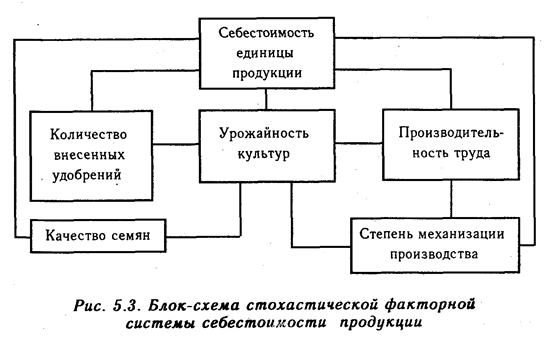
Создать детерминированную факторную систему — значит представить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.
Развитие детерминированной системы достигается за счет детализации комплексных факторов. Элементные факторы не раскладываются на множители, т. к. по содержанию они однородны. С развитием системы комплексные факторы детализируются на менее общие, постепенно приближаясь по своему аналитическому содержанию к простым факторам.
Систематизация факторов позволяет более глубоко изучать взаимосвязь факторов при формировании величины изучаемого показателя. Это имеет важное значение на других этапах экономического анализа хозяйственной деятельности.
Одна из задач факторного анализа — моделирование взаимосвязей между результативными показателями и факторами, которые определяют величину.
Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторным выражается в форме конкретного математического уравнения.
Типы факторных моделей в детерминированном анализе:
1) мультипликативные. Данный тип моделей применяется в тех случаях, когда результативный показатель представляет собой произведение нескольких факторов;
2) аддитивные. Используются в случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей;
3) кратные модели. Используются тогда, когда результативный показатель получают делением одного фактора на величину другого;
Моделирование мультипликативных факторных систем в экономическом анализе хозяйственной деятельности осуществляется путем последовательного расчленения факторов исходной системы на факторы — сомножители. Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации зависит от цели исследования, возможностей детализации, формализации показателей.
Моделирование аддитивных факторных систем осуществляется путем расчленения факторов исходной модели на составные элементы.
Способы преобразования кратных моделей:
1) метод удлинения (предусматривает удлинения числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей);
2) метод сокращения (представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель. Получается конечная модель того же типа, но с другим набором факторов);
3) метод расширения (предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Этот способ моделирования широко применяется в анализе). Результативные показатели могут быть разложены на составные элементы различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, профессиональных знаний и навыков исследователя.
7. Детерминированное моделирование факторных систем
7. Детерминированное моделирование факторных систем
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования факторных систем заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Моделирование себя как трейдера
Моделирование себя как трейдера Вышесказанное объясняет, почему модели идеального трейдера должны возникать на основе собственного торгового опыта, а не фантазий. Изучая свои прошлые результаты торговли, я нашел, что моими самыми успешными сделками были сделки
2. Моделирование инвестиционных проектов
2. Моделирование инвестиционных проектов Цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется. Иоганн Гете Моделирование инвестиционных проектов по сути является работой с механизмом расчетов различных параметров и
2.5. Моделирование рисков
2.5. Моделирование рисков Определение, расчет и анализ факторов риска – одна из главных частей инвестиционного проектирования. Созданный проект является, в сущности, прогнозом, который показывает, что при определенных значениях исходных данных могут быть получены
Моделирование поведения простых портфелей
Моделирование поведения простых портфелей Пример с подбрасыванием монеты должен убедить вас в ценности диверсификации активов. В реальном мире инвестиций вы сталкиваетесь с выбором активов, который кажется безграничным. Из этих активов можно создать буквально
Глава I ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРЕДПРИЯТИЯ
Глава I ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРЕДПРИЯТИЯ Динамическое моделирование предприятия представляет собой исследование предприятия как информационной системы с обратной связью; оно предусматривает применение моделей для проектирования усовершенствованных форм
27. Экономико-математическое моделирование
27. Экономико-математическое моделирование Применение математики в экономике принимает форму экономико-математического моделирования. С помощью экономико-математической модели изображается тот или иной действительный экономический процесс. Такая модель может быть
68. Моделирование
68. Моделирование Признанной группой расчетных методов является моделирование. В общем случае модель – это допустимо упрощенный аналог реальной или предполагаемой к созданию системы, используемой в процессе исследования. При проведении анализа используются два класса
Моделирование по методу Монте-Карло
Моделирование по методу Монте-Карло Моделирование по методу Монте-Карло представляет собой способ определения силы системы и отвечает на вопросы: «Что могло бы произойти, если бы прошлое было чуть другим?» или «Что может принести будущее?» Вы можете рассматривать метод
Моделирование
Моделирование Моделирование – это метод обучения, сочетающий в себе анализ конкретных ситуаций с ролевыми играми и позволяющий максимально приблизиться к реальности в условиях учебной аудитории. Цель метода заключается в том, чтобы способствовать переносу знаний,
МОДЕЛИРОВАНИЕ КОМПЕТЕНЦИЙ
МОДЕЛИРОВАНИЕ КОМПЕТЕНЦИЙ Моделирование компетенций сводит данные по организационному проектированию и управлению показателями труда, чтобы установить, какие навыки или компетенции требуются для выполнения определенных работ. Оно способствует принятию решений по
Шаг 7. Имитационное моделирование
Шаг 7. Имитационное моделирование Имитационное моделирование – это один из методов определить реализуемость и эффективность предлагаемых вариантов перестроенных процессов. Имитация также может применяться для проверки логики и согласованности процессов перед их
Моделирование
Моделирование Большинство современных моделей науки управления настолько сложны, что применять их можно только с помощью компьютерной техники. Однако сама концепция модели очень проста. По определению Р. Шеннона «Модель – это представление объекта, системы или идеи в
Моделирование успешного коучинга
Моделирование успешного коучинга Перенос моделей из других областей Мы покажем вам «сборную солянку» из различных коучинговых программ. Посмотрите их, чтобы понять, как ведется работа у других и что можно внедрить в своем бизнесе.Под словом «коучинг» можно выдавать
Моделирование процесса социального предпринимательства
Моделирование процесса социального предпринимательства Социальное предпринимательство можно рассматривать с точки зрения отдельного предпринимателя, предприятия или контекста, в рамках которого они действуют. Однако в любом случае социальное предпринимательство
Моделирование
Моделирование В начале работы над проектом почти всегда возникает ряд важных вопросов, связанных с реализацией той или иной технологии. Моделирование — важная методика, которая поможет получить необходимые ответы.О чём пойдёт речьСоздание прототипа — важный этап,
Моделирование нового средства рекламы
Моделирование нового средства рекламы В то время как Интернет развивался, становясь средством всемирной связи, Yahoo! быстро становилась одним из немногих мест, где множество людей, искавших возможность связаться друг с другом, могли регулярно регистрироваться. Эти люди
Детерминированное моделирование факторных систем
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования факторных систем заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Систематизация факторов и детерминированное моделирование факторных систем



Системный подход в экономическом анализе деятельности организации вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и соподчиненности, что достигается с помощью систематизации. Систематизация в целом – это размещение изучаемых явлений или объектов в определенном порядке с выявлением их взаимосвязи и подчиненности.
Одним из способов систематизации факторов является создание детерминированных факторных систем. Создать факторную систему – значит представить изучаемый объект в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.
Детерминированный факторный анализ – это методика исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов. Это обуславливает выделение типов факторных систем: мультипликативные, кратные, аддитивные и смешанные (см. п. 2.6).
При моделировании детерминированных факторных систем, как уже отмечалось выше, необходимо выполнять ряд требований:
— факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями;
— факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями;
— каждые показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность;
— факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это означает, что в ней должна учитываться соразмерность измерений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
Необходимо отметить, что существующие приемы детерминированного факторного анализа (цепной подстановки, индексный, абсолютных и относительных разниц, интегральный и логарифмирования) имеют различные области своего применения. Основные приемы детерминированного факторного анализа и сфера их применения систематизированы в виде таблице 3.1.
Таблица 3.1 – Область применения основных приемов детерминированного факторного анализа
| Прием | Модели | |||
| Мультипликативные | Аддитивные | Кратные | Смешанные | |
| Цепной подстановки | + | + | + | + |
| Индексный | + | — | + | — |
| Абсолютных разниц | + | — | — | 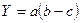 |
| Относительных разниц | + | — | — | 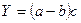 |
| Интегральный | + | — | + | 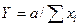 |
| Логарифмирования | + | — | — | — |
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.
Моделирование– это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения.
Моделирование мультипликативных факторных систем в экономическом анализе осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели мультипликативного типа, как:
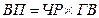
где 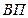
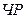
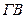
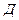
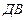
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.
Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный момент в экономическом анализе. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Систематизация факторов в анализе хозяйственной деятельности
Необходимость и значение систематизации факторов. Основные способы систематизации факторов в детерминированном и стохастическом анализе.
Системный подход в АХД вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и соподчиненности, что достигается с помощью систематизации. Систематизация в целом — это размещение изучаемых явлений или объектов в определенном порядке с выявлением их взаимосвязи и подчиненности.
Одним из способов систематизации факторов является создание детерминированных факторных систем.Создать факторную систему — значит представить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.
Например, объем валовой продукции промышленного предприятия можно представить в виде произведения двух факторов первого порядка: среднего количества рабочих и среднегодовой выработки продукции одним рабочим за год, которая в свою очередь зависит непосредственно от количества отработанных дней одним рабочим в среднем за год и среднедневной выработки продукции рабочим. Последняя также может быть разложена на продолжительность рабочего дня и среднечасовую выработку (рис. 5.2).
Однако необходимо заметить, что развитие факторных систем до необходимой глубины связано с некоторыми методологическими трудностями и прежде всего с трудностью нахождения факторов общего характера, которые можно было бы представить в виде произведения, частного или алгебраической суммы нескольких факторов. Поэтому обычно детерминированные системы охватывают наиболее общие факторы. Между тем исследование более конкретных факторов в АХД имеет существенно большее значение, чем общих.
Отсюда следует, что совершенствование методики факторного анализа должно быть направлено на взаимосвязанное изучение конкретных факторов, которые находятся, как правило, в стохастической зависимости с результативными показателями.
Большое значение в исследовании стохастических взаимосвязей имеетструктурно-логический анализ связи между изучаемыми показателями. Он позволяет установить наличие или отсутствие причинно-следственных связей между исследуемыми показателями, изучить направление связи, форму зависимости и т.д., что очень важно при определении степени их влияния на изучаемое явление и при обобщении результатов анализа.
Анализ структуры связи изучаемых показателей в АХД осуществляется с помощью построенияструктурно-логической блок-схемы, которая позволяет установить наличие и направление связи не только между изучаемыми факторами и результативным показателем, но и между самими факторами. Построив блок-схему, можно увидеть, что среди изучаемых факторов имеются такие, которые более или менее непосредственно воздействуют на результативный показатель, и такие, которые воздействуют не столько на результативный показатель, сколько друг на друга.
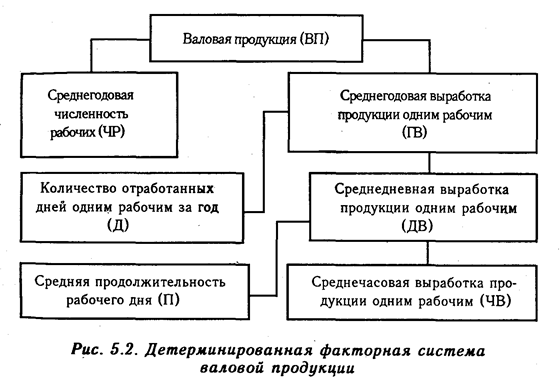
Например, на рис. 5.3 показана связь между себестоимостью единицы продукции растениеводства и такими факторами, как урожайность культур, производительность труда, количество внесенного удобрения, качество семян, степень механизации производства.
Прежде всего необходимо установить наличие и направление связи между себестоимостью продукции и каждым фактором. Безусловно, между ними существует тесная связь. Непосредственное влияние на себестоимость продукции оказывает в данном примере только урожайность культур. Все остальные факторы влияют на себестоимость продукции не только прямо, но и косвенно, через урожайность культур и производительность труда. Например, количество внесенных удобрений в почву содействует повышению урожайности культур, что при прочих одинаковых условиях обусловливает снижение себестоимости единицы продукции. Однако необходимо учитывать и то, что увеличение количества внесенных удобрений приводит к росту суммы затрат на гектар посева. И если сумма затрат возрастает более высокими темпами, чем урожайность, то себестоимость продукции будет не снижаться, а повышаться. Значит, связь между этими двумя показателями может быть и прямой, и обратной. Аналогично влияет на себестоимость продукции и качество семян. Приобретение элитных, высококачественных семян вызывает рост суммы затрат. Если они возрастают в большей степени, чем урожайность от применения более высококачественных семян, то себестоимость продукции будет увеличиваться, и наоборот.
Степень механизации производства влияет на себестоимость продукции и прямо, и косвенно. Повышение уровня механизации вызывает рост затрат на содержание основных средств производства. Однако при этом увеличивается производительность труда, растет урожайность, что содействует снижению себестоимости продукции.
Исследование взаимосвязей между факторами показывает, что из всех изучаемых факторов отсутствует причинно-следственная связь между качеством семян, количеством удобрений и механизацией производства. Отсутствует также непосредственная обратная зависимость данных показателей от уровня урожайности культуры. Все остальные факторы прямо или косвенно влияют друг на друга.
Таким образом, систематизация факторов позволяет более глубоко изучить взаимосвязь факторов при формировании величины изучаемого показателя, что имеет очень важное значение на следующих этапах анализа, особенно на этапе моделирования исследуемых показателей.