Что значит сочетательное свойство сложения в математике

Свойства сложения и вычитания

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

Источник

Сочетательный закон сложения – правило

Многие ученики путают понятия сочетательного закона сложения и сочетательного свойства сложения. Насколько это допустимо и как не путаться – разберемся вместе.

Сумма чисел

Сначала вспомним, что такое сумма чисел. Если два числа разбить на единицы, а потом все эти единицы свести в одно число, то получится сумма. Примерно так объясняют сумму в младших классах, иногда приводя примеры на сложение фруктов, конфет или канцелярских принадлежностей.

Такие объяснения правильны, но они не подходят для курса средней школы. Чем старше ученик, тем более глубокое и емкое определение ему нужно знать.

Поэтому в математике старших классов используют другое определение. Сумма это движение числа по числовой прямой вправо. На самом деле, число может двигаться и влево, при сложении отрицательных чисел. Но принято говорить «вправо», поскольку такие суммы сначала преобразовываются в разность

Законы сложения

Законов сложения всего два. Это сочетательный и переместительный. Сочетательный закон гласит, если в примере есть несколько слагаемых, то можно сложить два из них между собой, а потом к результату прибавить оставшееся слагаемое. Таким образом, можно складывать сколько угодно большие выражения. Применение этого свойства основано на сочетании слагаемых, откуда и взято это название.

Переместительный закон имеет следующую формулировку: «От перемены мест слагаемых сумма не меняется». Вне зависимости от того, как расположены слагаемые в примере, итоговое значение не измениться. Если подумать, то это логично. Какая разница, высыпать в корзину 10 фруктов, а потом еще 8 или сначала 8, а потом 10.

Разве количество фруктов в корзине от этого измениться? Конечно, нет.

Свойства сложения – это проявление простейшей логики в математике. Они доказывались опытным путем еще математиками Древней Греции. На сегодняшний день кажется невозможным не использовать их, поэтому свойства нужны скорее не для использования и запоминания, а для теоретического подтверждения того, что все и так знают. Ведь всеобщее знание это не аргумент в математике всегда нужно ссылаться на какие-то законы, аксиому и теоремы, чтобы доказать правильность решения. При этом свойство и закон сложения это одно и то же. Никакой разницы между ними нет.

Сочетательный закон

Сочетательный закон интересен тем, что может значительно ускорить выполнение сложения. Рассмотрим некоторые принципы быстрого счета, основанные на сочетательном законе.

3,72-5+5,28+17,8+9,2 – иногда проще разделить целые и дробные части дробей, чтобы ускорить счет.

Что мы узнали?

Мы поговорили о том, что такое сумма. Узнали о двух основных свойствах сложения и выделили правило сочетательного закона сложения. Привели несколько способов быстрого счета, основанных на сочетательном законе сложения. Рассмотрели несколько простых примеров.

Источник

Базовые свойства

Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:

Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.

Нахождение суммы многозначных чисел

Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.

Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.

Прибавление дробей и смешанных значений

Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.

При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.

Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).

Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:

В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.

Складывание векторов, пределов и матриц

Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:

Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.

Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.

Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.

Сложение в двоичной системе счисления

В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.

Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.

Источник

Сочетательное свойство сложения

Всего получено оценок: 79.

Всего получено оценок: 79.

Свойства сложения – это первый шаг к ускорению счета. Ученик, владеющий всеми приемами быстрого сложения, имеет больше времени для сложных задач и проверки своего решения. Поэтому имеет смысл рассмотреть свойства сложения еще раз, чтобы правильно применять их на практике

Что такое сложение?

Для начала вспомним, что такое вообще сложение? Сложение это одна из первых операций, которые изучают в школе, а иногда даже в детском саду. Как правило, сложение объясняют на примере фруктов.

Если взять 3 груши и 2 яблока, сложить их в корзину, то груши это первое слагаемое, яблоки второе, а общее количество фруктов в корзине – сумма. Это определение нельзя назвать неправильным, но ученики растут, как растут и используемые числа. Сложно представить себе сложение сотен тысяч фруктов.

Поэтому в математике используют другое определение, которое гласит, что сложение это перемещение точки на числовой прямой в право.

Многие знания усложняются со временем. Так, если в начальной школе ученикам говорят, что отрицательный результат сложения это ошибка, то в 5 классе все уже знают, что такой ответ возможен. Так и с определением свойств сложения. Обычных фруктов просто не хватит для того, чтобы представить себе большие числа. Поэтому в старших классах уходят к теоретическим определениям.

Свойства сложения

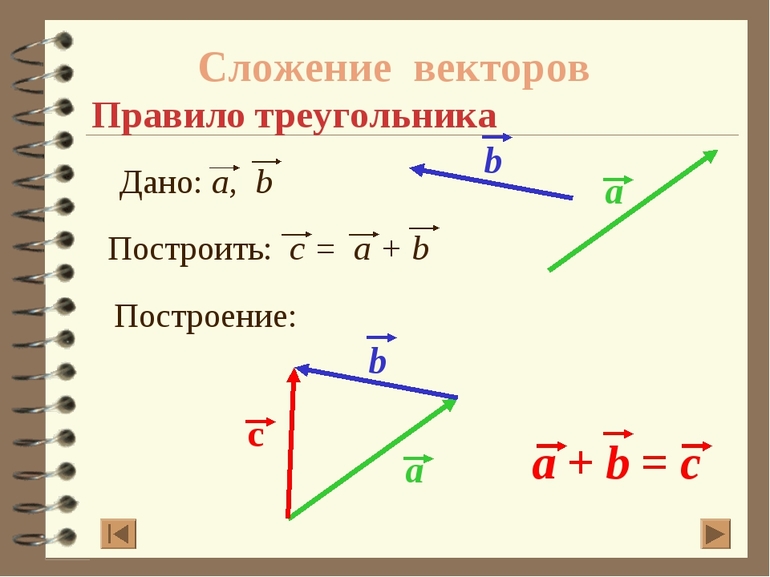
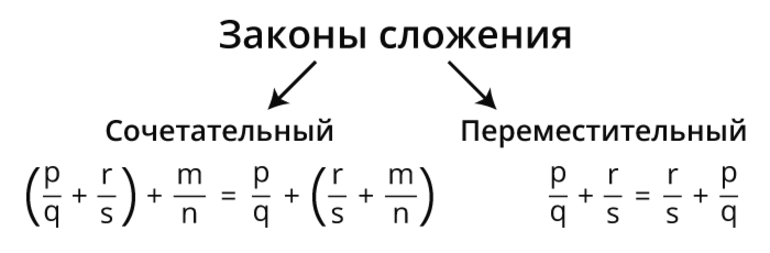
Выделяют переместительное и сочетательное свойство. Переместительное свойство говорит нам о том, что от перемены мест слагаемых сумма не поменяется.

Сочетательное свойство утверждает, что в примерах, где два и более множителя, сложение может производиться в любом порядке. Главное в этом случае правильно сгруппировать слагаемые, чтобы ускорить вычисления, а не затруднить его еще сильнее. Самый простой вариант это смотреть на количество единиц в числе. В первую очередь нужно складывать те числа, сумма единиц в которых равняется 10, например 29 и 31 в сумме дадут 60.

После этого складывают целые десятки и только потом все остальное. Это наиболее простой и быстрый путь решение примеров на сложение.

На самом деле даже не каждый профессор сможет отличить применение сочетательного свойства от переместительного. Они крайне похожи, некоторые математики считают даже, что сочетательное свойство является продолжением переместительного. По той же причине учителя редко просят отличить применение в задаче одного свойства от другого. Нужно просто уметь пользоваться обоими.

Пример

Примеры сочетательного свойства сложения найти не трудно. Практически в каждом примере используется это свойство.

15*3+5-13-17-2-16-2 – для начала выполним умножение.

45+5-13-17-2-16-2 – теперь сгруппируем члены так, чтобы вычислить результат как можно быстрее. Для этого нужно вспомнить, что разность можно представить, как сумму отрицательных чисел. В нашем случае просто вынесем минус за знак скобок.

45+5-13-17-2-16-2=(45+5)-(13+17)-(2+2+16) – теперь выполним вычисления в скобках и найдем окончательный результат

Вот такой ответ получился у достаточно большого примера. Не стоит пугаться простых ответов вроде 0 или 1. Иногда составители примеров таким образом путают учеников.

Что мы узнали?

Мы поговорили о сложении, выделили сочетательное и переместительное свойства сложения. Поговорили о различиях этих свойств, а также о правильном применении сочетательного свойства сложения. Решили небольшой пример, чтобы показать применение сочетательного свойства на практике.

Источник

Общие сведения

Сложение является одной из базовых арифметических операций в математике. Оно изучается во втором классе общеобразовательной школы. Существует всего 2 правила: переместительный и сочетательный закон сложения. Однако многие ученики часто их путают. Разобраться в этом помогут специалисты. Они разработали специальную методику, позволяющую быстро запомнить различие между ними.

Однако для изучения алгоритма нужно знать базовые термины и определения. К ним относятся:

Сложение состоит минимум из трех элементов: двух слагаемых (одно из них увеличивается на другое) и результата. Последний называется суммой. На примере это выглядит так: 5+9=14, где 5 — I слагаемое, 9 — второй элемент-слагаемое или число, на которое нужно увеличить первое слагаемое, а 14 — их сумма.

Переместительное правило

Переместительное (коммутативное) правило является очень простым для понимания. Оно формулируется следующим образом: если поменять местами слагаемые, их сумма не изменится. Математическая форма записи закона выглядит следующим образом: q+w=s.

На практическом примере правило реализуется в таком виде: 5+6=6+5=11. Последнее числовое выражение очень легко проверить. Для этого достаточно воспользоваться обыкновенным калькулятором. При сложении 5 и 6 он покажет величину, равную 11. Следует отметить, что таким образом и доказывается закон переместительного свойства сложения.

Прием практической реализации для доказательства правил и утверждений применяется очень часто. Это и есть оптимальная методика, позволяющая выяснить работоспособность того или иного утверждения. Далее необходимо рассмотреть сочетательный закон сложения.

Сочетательный закон

Сочетательное правило сложения возможно применить, когда числовое выражение включает в свой состав от трех и более слагаемых. Сочетательный закон сложения во 2 классе можно сформулировать следующим образом: слагаемые, входящие в состав выражения, можно для удобства складывать в любом порядке.

Очень часто правило называют ассоциативным свойством операции сложения. Ее математическая запись имеет такой вид: p+r+s=(p+s)+r=(s+r)+p=z. Чтобы доказать утверждение, нужно решить пример «2+9+8+1». Его специалисты рекомендуют решать по такому алгоритму:

К сочетательному свойству также можно применить и переместительное (коммуникативное) правило. Этим приемом очень часто пользуются специалисты. Кроме того, по-другому ассоциативный закон называется методом группировки чисел. Далее нужно рассмотреть методику применения двух законов на практике.

Методика применения

Методика использования правил сложения зависит от конкретного примера. Однако специалисты рекомендуют придерживаться следующего алгоритма нахождения результатов числовых выражений:

Сочетание элементов можно выполнять несколько раз, т. е. вычислить сначала одно значение, а потом опять перегруппировать выражение. Перемену мест слагаемых можно производить в несколько заходов.

Кроме того, законы сложения можно применять не только для целых чисел, но и для дробных. Для совершенствования качества усвоения теоретического материала рекомендуется придумать примеры и решить их.

Некоторые ученики часто путают принадлежность распределительного правила к суммации двух и более величин. Этого делать не нужно, а требуется запомнить, что у сложения только 2 закона, но не 3. Последний принадлежит только операциям деления и умножения.

Переместительное и сочетательное свойства можно применять и для вычитания. Далее необходимо на практическом примере разобрать использование правил сложения и методику их применения.

Пример решения

Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:

Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.

Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.

Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.

Источник