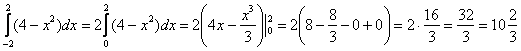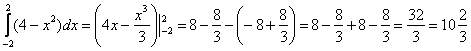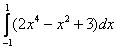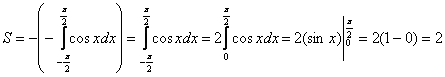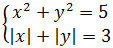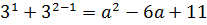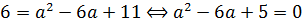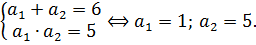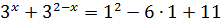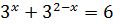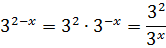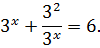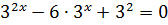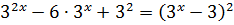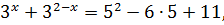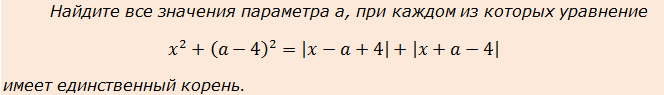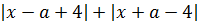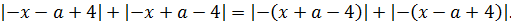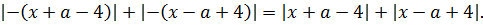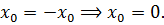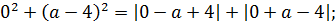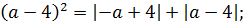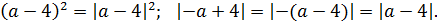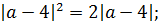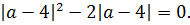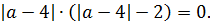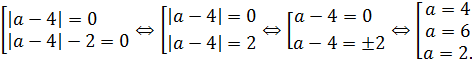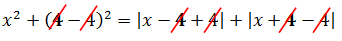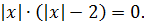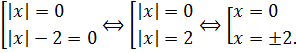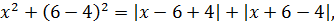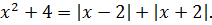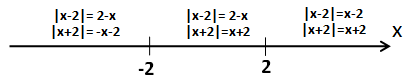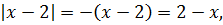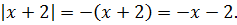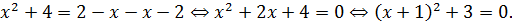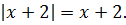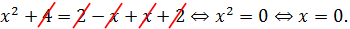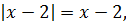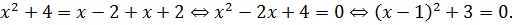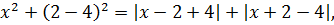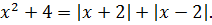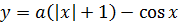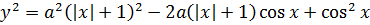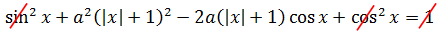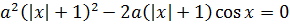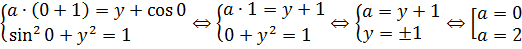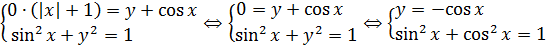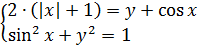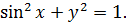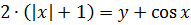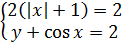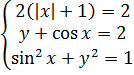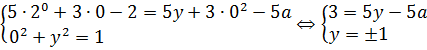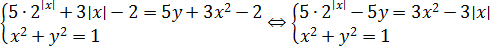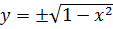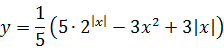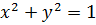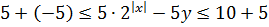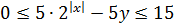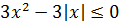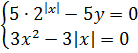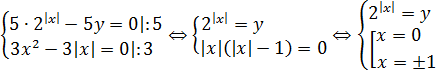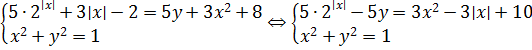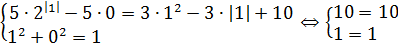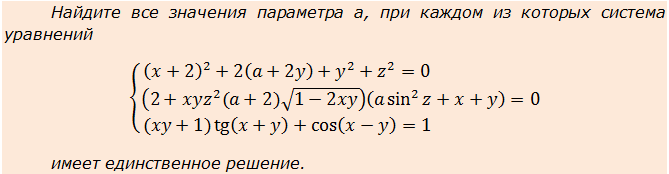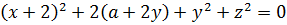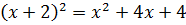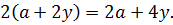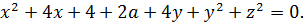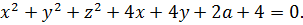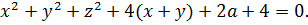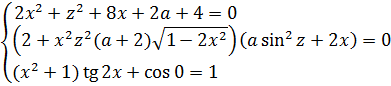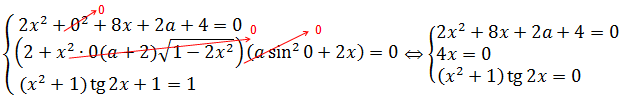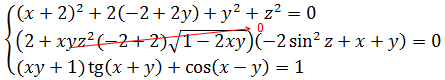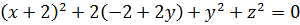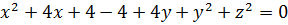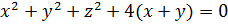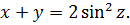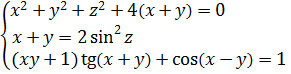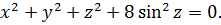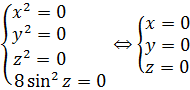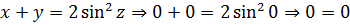Что значит симметрична относительно нуля

№47 Виды симметрии периодических функций.

Различают следующие виды симметрии периодических несинусоидальных функций.

1) Нечетная симметрия: функция симметрична относительно начала координат и удовлетворяет условию f(t)=-f(-t) (рис. 47.1).

Функции, обладающие нечетной симметрией, получили название нечетных. В разложении таких функций содержатся только синусные составляющие отдельных гармоник Bk и отсутствуют постоянная составляющая A0 и косинусные составляющие отдельных гармоник Сk:

При определении коэффициентов ряда Фурье нечетной функции интегрирование в формуле достаточно выполнить за половину периода T/2:

2) Четная симметрия: функция симметрична относительно оси ординат и удовлетворяет условию f(t)=f(-t) (рис. 47.2).

Функции, обладающие четной симметрией, получили название четных. В разложении таких функций содержатся только постоянная составляющая А0 и косинусные составляющие отдельных гармоник Ck и отсутствуют синусные составляющие отдельных гармоник Вк:

При определении коэффициентов ряда Фурье четной функции интегрирование в формулах достаточно выполнить за половину периода:

3) Косая симметрия: функция симметрична относительно оси абсцисс при смещении ее положительной части [f(t)>0] или отрицательной части [f(t)

Источник

Метод решения определенного интеграла от четной функции по симметричному относительно нуля отрезку

Рассмотрим определенный интеграл вида

.

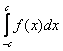
Легко заметить, что отрезок интегрирования [-c; c] симметричен относительно нуля.

Если подынтегральная функция 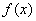является чётной, то интеграл

можно вычислить по половине отрезка, а результат – удвоить:

.

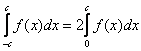
Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом:

Вычислить определенный интеграл

О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим один раз: функция является чётной, если для неё выполняется равенство .

Как проверить функцию на чётность? Нужно вместо«икс» подставить .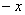

В данном случае: и ,

значит, данная функция является чётной.

Согласно правилу, на симметричном относительно нуля отрезке [-2; 2] наш интеграл от чётной функции можно вычислить следующим образом:

А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….

Любая чётная функция, в частности , симметрична относительно оси OY:

численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а, значит, и симметричности её графика относительно оси OY, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые же половинки! Именно поэтому справедливо действие

Аналогичная история происходит с любой чётной функцией 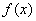по симметричному относительно нуля отрезку:

Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:

Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже. Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает. Короткий разминочный пример для самостоятельного решения:

Вычислить определенный интеграл

Полное решение и ответ в конце урока.

Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Иллюстрация к Примеру 1 дана только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:

1) Вычислить определенный интеграл

.

2) Вычислить площадь плоской фигуры, ограниченной линиями

, и осью OX на интервале .

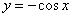
Это две разные задачи!Об этом уже говорилось в статье Как вычислить площадь плоской фигуры? Сначала разберемся с первым пунктом:

1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:

Определенный интеграл получился отрицательным и так бывает!

3) Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:

На отрезке график функции расположен ниже оси OX, поэтому:

Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (см. также Пример 3 урока Определенный интеграл. Как вычислить площадь фигуры).

Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок, и удвоили интеграл.

Источник

Симметрия чисел

Симметрия чисел
1. Введение
В нашем мире все взаимосвязано, похоже друг на друга, имеет одинаковые или схожие параметры. Часто эти свойства называют симметрией. В «Кратком Оксфордском словаре» симметрия определяется как «Красота, обусловленная пропорциональностью частей тела или любого целого, равновесием, подобием, гармонией, согласованностью». [1 ] Очень часто симметрия проявляется в математике и физике. В физике свойства симметрии ярко проявляются в квантовой механике и ее математическом аппарате, например Уравнении Шредингера [ 2]. В математике существует специальный математический аппарат, оперирующий понятиями подобия и симметрии. Этот математический аппарат называется теорией групп [3]. Одним из практических применений симметрии в математике, является шифрование с открытым ключом “RSA” [4].

2. Матрица остатков простого числа

Рассмотрим определение вычета и сравнения по модулю. Вот определение, приведенное в современном толковом словаре. Число “ a “ называется вычетом числа “ b “ по модулю “ m “, если разность “ a – b “ делится на “ m “ ( a, b, m > 0 – целые числа ). То есть “ a “ сравнимо с “ b “ по модулю “ m “.

Это означает, что если “ a “ не делится нацело на “ m ”, то “ b “ остаток от деления “ a “ на “ m “. Два целых числа “ a “ и “ b “ сравнимы по модулю натурального числа “ m “, если при делении на “ m “ они дают одинаковые остатки.
Возьмем простое целое число и обозначим его “ b ”. Множество целых чисел в интервале (1,2,3,…b-1) обозначим “ B “. Если это множество записать в виде столбца, в порядке возрастания снизу вверх, то получим матрицу столбец. Все числа в этом столбце расположены одно за другим, их количество равно “ b – 1 “. Обозначим этот столбец номером “ 1 “. Каждое число из множества “ B “ возведем в квадрат и разделим на “ b “ с остатком. Полученные в результате деления остатки запишем в столбец. Обозначим этот столбец номером “ 2 “ и расположим его справа от столбца номер “ 1 “. Нужно расположить остатки так, чтобы они соответствовали числам, возводимым в квадрат, и находились с ними на одной прямой. После этого каждое число из множества “ B “ возведем в третью степень и разделим на “ b “ с остатком. Из полученных остатков сформируем столбец под номером “ 3 “, по аналогии со столбцом номер “ 2 “. Далее по аналогии возводим в следующую степень и находим остатки от деления на “ b “. Действия выполняем до тех пор, пока показатель степени, в которую возводим числа из множества “ B “, меньше “ b “. В результате получим квадратную матрицу размером (b-1) x (b-1).

Пример такой квадратной матрицы для простого целого числа “ b = 23 “ представлен на рис.1.

Рис. 1 Матрица остатков простого целого числа b = 23.

Полученная матрица обладает удивительными свойствами:

— Наглядно видно, что последний столбец матрицы состоит из одних единиц. Это полностью соответствует тесту простоты Ферма. A n-1 ≡ 1(mod N) [5].
— Следует отметить, что столбец с номером (b-1)/2 ( “ b “ минус 1 деленное на 2 ) состоит только из двух значений множества “ B “. Это значения 1 и ( b-1).
— Значения чисел, множества “ B “, в столбцах, симметричны относительно середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2.
— Виды симметрии для различных столбцов различны.
— Для столбцов с четными номерами, значения равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, совпадают. Для матрицы, изображенной на рис. 1, остаток от 11 в квадрате, деленное на 23 и остаток от 12 в квадрате, деленное на 23, совпадают и равны 6.
— Для столбцов с нечетными номерами, значения, равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, в сумме всегда равны “ b “. Для матрицы, изображенной на рис. 1, остаток от 11 в третьей степени, деленное на 23, равен 20, остаток от 12 в третьей степени, деленное на 23, равен 3. В сумме эти два остатка равны 23, т.е. равны “ b “.

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 1, присущи матрицам, построенным по таким же правилам для других простых целых чисел.

3. Матрица остатков составного числа

Матрица, рассмотренная в разделе 2, характеризует симметрию простых чисел. Для составных чисел матрица, построенная по тем же самым правилам, существенно отличается. Она наследует свойства матрицы простого числа, но приобретает и новые свойства. Рассмотрим составное число, являющееся произведением двух простых чисел “ x “ и “ y “. Точно так же величину числа обозначим “ b “, а множество всех чисел, в интервале (1,b-1), обозначим “ B “. Рассмотрим составное число “ b = 35 “, являющееся результатом перемножения простых чисел “ x = 5 “ и “ y = 7 “. Построим матрицу остатков различных степеней, для числового интервала (35-1). Матрица остатков представлена на рис. 2

Рис. 2 Матрица остатков составного числа b = 35.
Часть свойств унаследована от матрицы остатков простого числа. Так например, значения чисел, присутствующих в столбцах, симметричны относительно середины значений числового интервала, т.е. значений (b-1)/2 и (b+1)/2.

Матрица, изображенная на рис. 2, несет в себе новые свойства:

— Значения строк матрицы, у которых в первом столбце присутствуют величины кратные делителям составного числа, принимают числовые значения кратные делителям составного числа и никогда не равны 1. Например, в матрице рис. 2, строка 5, во втором столбце, имеет значение 25, в третьем 20, в четвертом 30 и так далее. Все эти значения кратны 5.
— Если исключить строки, значения которых кратны делителям числа “ b “, то обязательно найдутся два столбца, в которых остальные значения равны 1. Например, на рис. 2 это столбцы с номерами 12, 24.
— Из этих двух выбранных столбцов, наибольший номер столбца равен произведению (x-1) на (y-1). Т.е. если от каждого из сомножителей, вычесть 1 и перемножить их, то получим номер наибольшего выбранного столбца. Для матрицы на рис. 2 сомножители числа “ b “ равны 5 и 7. Если от каждого из них отнять 1 и перемножить, то получим (5-1) x (7-1) = 24. Это как раз номер наибольшего выбранного столбца. Следует отметить, что в данном случае, номер столбца равен функции Эйлера, значение которой равно (x-1) x (y-1) = ѱ(n). [6].
— Во втором столбце обязательно присутствуют четыре значения равные 1. Для матрицы остатков простого числа и значений множества “ B “равных (1,b-1), величины во втором столбце принимают значение 1. Для матрицы остатков составного числа, обязательно существуют еще два числа множества “ B “, при возведении которых в квадрат и делении на “ b “, остаток равен 1. На рис. 2 это числа 6 и 29.
— Всегда присутствуют пары чисел, множества “ B “, следующих друг за другом, значения которых, кратны делителям “ x “ и “ y “ числа “ b”. Для матрицы на рис. 2 это пары ( 14, 15 ) и ( 20, 21 ).

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 2, присущи матрицам, построенным по таким же правилам для других составных целых чисел.

4. Факторизация чисел

Если рассмотреть метод шифрования с открытым ключом RSA [4], то его использование основано на существовании взаимно противоположных отображений в матрице остатков составного числа. Если взять составное число “ b “, в его матрице остатков всегда существуют два столбца “ c “ и “ d “, для которых выполняются следующие условия:

(b1**c) ≡ c1( mod b); (c1**d) ≡ d1( mod b ); b1 = d1

где b1, c1, d1 числовые значения в столбцах 1, c, d.

То есть для составного числа “ b “ всегда существует два числа “ c “, “ d “ из диапазона (1,b-1), для которых справедлива последовательность действий:
— Определим остаток любого числа “ b1 “, из диапазона (1,b-1), возведенного в степень “ c “ и деленного на “ b “. Обозначим этот остаток “ c1 “.
— Полученный остаток “ c1 “ возведем в степень “ d “ и разделим на “ b “ с остатком. Обозначим этот остаток “ d1 “.
— Полученный остаток “ d1 “ всегда равен “ b1 “.
Для алгоритма шифрования RSA, (c,b) – открытый ключ, (d,b) – секретный ключ.

Рис. 3 Матрица остатков составного числа b = 33.

Рассмотрим матрицу остатков числа b = 33, рис. 3. Для этого числа c = 3, d =7. Возьмем любое число из первого столбца, например 8 и возведем его в 3 степень, остаток равен 17. Число 17 возведем в степень 7, остаток равен 8, т.е. этот остаток равен исходному числу из первого столбца.
RSA один из распространенных алгоритмов шифрования с открытым ключом. Вместе с совершенствованием методов шифрования, совершенствуются методы дешифровки секретных сообщений.
Часто задачу дешифровки для RSA, пытаются решить в лоб, т.е. найти делители базового составного числа. Эти методы называются факторизацией чисел. Кроме простого перебора значений и проверки чисел, используют метод квадратичного решета.

Основы этого метода в том, что часть остатков от возведения в квадрат и деления на число “ b “, являются полными квадратами чисел. На рис. 2 полными квадратами являются квадратичные остатки чисел (11, 12, 17), из первого столбца. Для нахождения делителей числа “ b “, необходимо из квадратичного остатка извлечь квадратный корень. Результат, т.е. квадратный корень, вычесть из числа “ b “ или сложить с числом “ b “. Будут получены числа кратные делителям числа “ b”. Используя алгоритм Евклида можно найти делители числа “ b “.
На рис. 2, для числа 11, квадратичный остаток равен 16. Извлекаем из 16 корень квадратный, он равен 4. К 11 прибавляем 4, получаем 15, число кратное делителю 5. От 11 отнимаем 4, получаем 7, число равное делителю 7.

Одним из самых современных методов факторизации чисел, является метод решета числового поля [7]. Этот метод позволяет сократить количество проверяемых значений и уменьшить время проведения вычислений. Использование метода решета числового поля и свойств матрицы остатков составного числа, позволяет достичь еще более весомых результатов.

Для экспериментальной проверки методов факторизации чисел можно использовать, так называемые, числа Мерсенна [8]. Эти числа представляют собой число 2 в степени “ n “, минус 1, где “ n “ натуральное число. Только ограниченное количество чисел Мерсенна являются простыми, остальные разлагаются на конечное количество делителей.
Как наглядный пример, один из делителей, числа 2 в степени 4099, минус 1, равен –
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717675764345142
549580867720367836084289513946899287311856029114297

Источник

Инвариантность или метод симметричных корней

Продолжаем знакомство с аналитическими способами решения сложных задач с параметрами, предлагающихся на различных пробниках и в настоящих вариантах ЕГЭ. В сегодняшнем материале будет рассмотрена новая группа задач, связанных с поиском значений параметра(ов), при которых имеется единственное решение задачи. Слово «единственное» в данной теме является ключевым. Один из самых распространённых методов решения таких задач — так называемый метод симметричных корней или, более научно, метод инвариантностей.

Типичные формулировки таких задач следующие: «Найдите все значения параметра а, при которых система уравнений имеет единственное решение.» Или: «Найдите все значения параметра а, при которых уравнение имеет единственный корень.»

Итак, пора познакомиться с инвариантностью. Что это за понятие? В переводе на русский язык слово «инвариантность» означает «неизменяемость». Неизменяемость чего-то по отношению к чему-то.)

В математике под инвариантностью понимается неизменяемость каких-либо выражений с переменными или функций по отношению к каким-либо преобразованиям над этими самыми переменными. Это может быть замена одной переменной на другую, смена знака и т.п. На словах, быть может, звучит не совсем понятно, но на деле всё гораздо проще.

Рассмотрим простой пример. Все мы с начальной школы знаем (я верю!) переместительное свойство сложения двух чисел:

Кто бы спорил, верно? От перестановки слагаемых сумма не меняется.) По-научному этот факт означает, что выражение a + b инвариантно относительно замены а на b и b на а. Можно сколько угодно менять буквы местами, а суть всего выражения от наших перестановок не изменится.)

Другой классический пример инвариантности – чётность. Если функция f(x) чётная, то, как мы знаем,

и тогда можно сказать, что функция f(x) инвариантна относительно замены x на –x.

Посмотрим на инвариантность в жизни?

Допустим у нас есть вот такое крутое уравнение:

Как нетрудно заметить, решений у него бесконечно много. Это, например, пары чисел (1;9), (5;5), (0;10), (-37;47), ну и так далее, можно писать до посинения.) Зачем, спрашивается? Пока — незачем. Бестолковое занятие, прямо скажем. Но, поскольку, как мы знаем, от перестановки слагаемых сумма не меняется, все эти решения объединяет одна важная особенность: если какая-то пара чисел (x₀; y₀) удовлетворяет данному уравнению, то автоматически и пара чисел (y₀; x₀) также обязательно ему удовлетворяет. Или в таких случаях говорят, что уравнение

инвариантно относительно замены x на y и y на x. Например, если пара (1;9) — решение, то автоматически и (9;1) — тоже решение. Понятно, я думаю.)

Идём дальше. Допустим, перед нами вот такая красивая система:

Кто умеет решать системы и в курсе, как раскрываются модули, тот без труда получит восемь её решений. Это пары:

Чем красива эта система? А тем, что она обладает сразу тремя типами инвариантностей!

Во-вторых, квадрат и модуль — чётные функции. Это значит, что суть системы не изменится от замены, например, x на -х. Поэтому, помимо пары (x₀; y₀) решением системы будет являться и пара (-x₀; y₀). Что выражается, например, парами (1; 2) и (-1; 2). Или (2; 1) и (-2; 1).

А теперь представим, что у нас есть какая-нибудь ооочень страшная система. И мы каким-то чудом установили, что эта система инвариантна относительно, скажем, замены x на y. При этом в задаче требуется, чтобы решение было единственным. Тогда обязательно должно выполняться равенство x = y. То есть, таким единственным решением может быть только пара чисел (x₀; x₀) (или (y₀; y₀), что в данном случае одно и то же).

И теперь во всей задаче мы всюду можем смело заменить игрек на икс (или наоборот) и перейти к одной переменной, что, скорее всего, сильно упростит дальнейшие выкладки.)

Но симметрия бывает не только относительно нуля. Если, скажем, уравнение не меняется относительно замены x на 2-x и должно иметь единственный корень, то обязательно должно выполняться равенство

x = 2 — x

То есть, этим единственным корнем может быть только единица. И теперьуже можно подставить x = 1 в исходное уравнение и определить все значения параметра, при которых единица является корнем.

А бывают и менее очевидные инвариантности. Например, относительно замены x на 1/x, откуда кандидатами на единственное решение могут быть только числа ±1. И так далее. Поиск таких закономерностей — порой процесс творческий и весьма интересный, и задачи такого типа предназначены для претендентов на высокие баллы.)

Сам процесс решения таких задач состоит из четырёх ключевых шагов.

1) Осмотр задачи и выявление инвариантных конструкций. Например, выражения x и -x, y и y-1 и т.п.

2) Нахождение решений-кандидатов на единственность. Делается это путём приравнивания этих самых инвариантных конструкций друг другу и решения получившегося уравнения.

3) Подстановка решений-кандидатов в исходную задачу и поиск соответствующих этим решениям значений параметра.

4) Проверка каждого найденных значений параметра на удовлетворение условий задачи.

Четвёртый шаг очень (ОЧЕНЬ!) важен в решении таких задач! Пояснения — ниже. На примерах.

Пример 1

Итак, речь идёт о единственном корне. Это явный призыв поискать в уравнении инвариантные конструкции.)

От икса зависит только левая часть. Выпишем её отдельно:

А теперь рассуждаем примерно так:

«У нас слева стоит сумма двух показательных выражений. Основания у них одинаковые — тройка. Что очень хорошо.) А вот показатели — разные. «Икс» и «два минус икс». Но! Если в первом слагаемом показатель х заменить на 2-х, а во втором — наоборот, 2-х заменить на х, то слагаемые просто поменяются местами, а суть всего выражения при этом не изменится.»

Совершенно верно! Данное уравнение инвариантно относительно замены х на 2-х! Другими словами, если какое-то число х₀ является корнем этого уравнения, то автоматически и число 2-х₀ также будет его корнем. )

У нас же, по условию, корень должен быть единственным. Поэтому это возможно в том и только в том случае, когда

Здесь выявлена так называемая симметрия относительно единицы.

Это означает, что если данное уравнение имеет единственный корень, то им может быть только единица. И теперь уже можно подставить х = 1 в исходное уравнение и определить, при каких же значениях параметра а оно будет выполняться. Подставляем:

Решаем данное квадратное уравнение. Проще всего по теореме Виета:

Получили два значения параметра — единицу и пятёрку. Но (внимание!) это пока что ещё не ответ, а лишь два возможных кандидата на ответ.) Теперь нам ещё предстоит сделать последний шаг — проверить каждое значение параметра а на выполнение условия единственности корня.

Специально акцентирую внимание на этом последнем шаге решения. Пропускать его ни в коем случае нельзя. Почему?

Казалось бы, всё классно: параметры найдены, и на этом решение задачи следовало бы закончить и записать ответ. Но… Вынужден открыть горькую правду. Всё дело в том, что найденные на третьем шаге значения параметра представляют собой лишь так называемое необходимое условие единственности решения. Но, к сожалению, не достаточное! Поясняю.

Поэтому последним (и обязательным!) шагом решения является проверка достаточности. Делается это так. Берётся каждое из найденных значений параметра и подставляется в исходную задачу. После чего решаем исходную задачу для каждого такого кандидата и устанавливаем, сколько решений в каждом случае получается. Тех кандидатов, при которых задача имеет более одного решения, безжалостно отсеиваем.)

Следует сказать, что последний шаг в подобных задачах зачастую наиболее трудоёмкий, потому что далеко не всегда при этом получаются уравнения и системы, решаемые стандартными алгебраическими преобразованиями — разложением на множители, приведением подобных, формулами тригонометрии, логарифмов и т.п. А требующие порой значительной изобретательности и искусства, я бы даже сказал. В чём мы лично убедимся на дальнейших примерах.)

Поэтому берём сейчас наши найденные значения параметра и подставляем в исходное уравнение.

Начнём с а = 1. Просто берём и подставляем в уравнение уже вместо «а» (а не икс!) единичку:

По правилам действий со степенями:

Перепишем наше уравнение с учётом данного факта:

Умножим обе части на знаменатель 3 х (это вполне безобидно, поскольку выражение 3 х положительно при любом x и никогда не равно нулю) и перенесём всё влево:

.

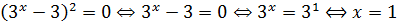
Итак, при a = 1 исходное уравнение действительно имеет своим единственным корнем единицу. Значит, a = 1 нас полностью устраивает и идёт в ответ.

Теперь разбираемся с пятёркой a = 5. Берём и подставляем в исходное уравнение пятёрку вместо a:

Получили уравнение, в точности эквивалентное случаю a = 1, имеющее, как уже установлено, единственный корень единицу. Значит, пятёрка нас также устраивает: a = 5.

Итак, мы полностью обосновали, что оба найденных значения параметра удовлетворяют условию достаточности, т.е. исходное уравнение действительно имеет единственный корень, и этот корень x = 1. И вот теперь можно с чистой совестью записывать окончательный ответ.)

Здесь проверка достаточности никак не сказалась на ответе. Повезло, хороший пример.) Но, ещё раз повторю, что этот шаг является обязательной частью решения таких задач. На примерах ниже мы воочию в этом убедимся.)

Пример 2

Здесь в нагрузку добавились ненавистные многими модули, но и мы тоже поднялись на следующий уровень.) Поскольку в задаче снова речь идёт о единственном корне, поищем инвариантности. Замечаем, что икс везде стоит внутри чётных функций — либо под модулем, либо в квадрате.

Напрашивается чётность. То есть, инвариантность относительно х и –х.)

Ну, с x 2 всё ясно — тут чётность очевидна. А вот с суммой модулей, стоящей в правой части, всё не так очевидно. Попробуем в выражение

вместо «икс» подставить «минус икс» и посмотрим, что из этого выйдет:

Как известно, модуль — тоже функция чётная и «сжигает» минус:

Итак, что мы видим? Мы видим, что от замены x на –x правая часть уравнения также не изменилась (просто модули поменялись местами :)). А это значит, что уравнение действительно инвариантно относительно х и –х. И, если оно имеет какой-то корень х₀, то и число –х₀ автоматически также будет корнем этого уравнения.

Поэтому для единственности эти два корня должны совпадать, т.е. необходимо выполнение условия

Значит, если данное уравнение имеет единственный корень, то им может быть только ноль. Подставляем число 0 в исходное уравнение вместо икса:

Для дальнейших упрощений воспользуемся чётностью квадрата и модуля:

Перепишем наше уравнение с учётом этих фактов:

Выносим один модуль за скобку:

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

Итак, получены три кандидата на ответ. При этих значениях параметра a исходное уравнение обязательно будет иметь одним из своих корней число 0. А вот будет ли число 0 единственным корнем или нет, нам и предстоит сейчас проверить. Проверяем теперь достаточность: устраиваем нашим кандидатам конкурсный отбор. 🙂

Порядок здесь роли не играет. Давайте начнём с четвёрки: a = 4. Подставляем вместо а в исходное уравнение четвёрку:

Все четвёрки благополучно посокращались и осталось лишь:

x 2 = |x| + |x| или x 2 — 2|x| = 0

Снова заменяем x 2 на |x| 2 и выносим один модуль за скобку:

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

Итак, что мы видим? Мы видим, что при a = 4 наше уравнение имеет не только корень x = 0, но и ещё два корня — два и минус два! О чём это говорит? О том, что при a = 4 уравнение имеет более одного корня (а именно — целых три). Стало быть, первый кандидат a = 4 не прошёл наш кастинг, поэтому с треском вылетает из дальнейшей борьбы и в ответ не идёт. 🙂

Эстафета передаётся следующему претенденту a = 6. Подставляем в наше уравнение шестёрку вместо параметра a. Получаем:

Получили типовое уравнение с модулями, решаемое путём раскрытия модулей по промежуткам. Предполагается, что народ, интересующийся нестандартными задачами с параметрами, решать такие уравнения уже умеет, поэтому здесь я опущу подробное описание решения этого уравнения (что, как, зачем и почему) и оформлю его достаточно сжато.

Раскроем модули на каждом промежутке и для наглядности подпишем их на рисунке.

Тогда имеем следующее:

В этом случае наше уравнение станет таким:

Ноль принадлежит рассматриваемому интервалу (-2; 2) и, стало быть, является первым корнем нашего уравнения.

И, наконец, на очереди третий случай.

3) x ≥ 2. В этом случае оба модуля раскрываются с плюсом:

Понятно, что левая часть всегда положительна, а значит, как и в первом случае, корней при x ≥ 2 у нашего уравнения также нет.

Итак, все случаи разобраны, и единственным корнем нашего уравнения является x = 0.

А теперь вспоминаем, что это уравнение мы получили и решили для a = 6. А это значит, что при a = 6 исходное уравнение действительно имеет единственный корень x = 0, а других корней, кроме нуля, не имеет (мы только что это доказали). Всё, a = 6 нас полностью устраивает, и шестёрка пошла прямиком в ответ.)

Третий пошёл!) Подставляем теперь a = 2:

Кандидата a = 2 можно сразу принять на работу в ответ без предварительного собеседования решения полученного уравнения. Почему? А потому, что, если взглянуть на получившееся уравнение, то можно увидеть, что оно отличается от уравнения, полученного для a = 6 только порядком слагаемых в правой части. То есть, по своей сути — ничем.) И, ясное дело, оно также имеет своим единственным корнем число 0.

Итак, a = 2 тоже подходит.)

Всё, задача полностью решена! 🙂

Так, с уравнениями более-менее потренировались. Двигаемся на следующий уровень и переходим теперь к системам.)

«Так-с… Модуль, тригонометрия — всё намешано в одну кучу, что как-то не особо обнадёживает. Можно, конечно, напрямую выразить из первого уравнения игрек

и подставить во второе, только что это даст? Всю эту белиберду ведь ещё и в квадрат возводить придётся!

Ну, хорошо. Подставляем теперь всё это барахло во второе уравнение вместо «игрек квадрат»:

И что тут можно сделать? О-па! Да тут же основное тригонометрическое тождество sin 2 x + cos 2 x = 1, которое можно сократить с единичкой справа.)

Ну, а потом что? Можно левую часть разложить на множители, отправив, к примеру, одну из скобок за скобки (да простит меня русский язык за тавтологию). Но что-то уж больно запутанно получается… Не факт, что удастся добраться до истины, совсем не факт… Стоп! Но у нас же говорится о единственном решении! А может, тут тоже есть что-то симметричное или инвариантное, что сделает решение куда проще?»

Немного присмотревшись к системе, можно снова заметить, что икс везде тусуется внутри чётных функций — модуль, косинус, квадрат синуса….

А это означает, что вместе с какой-то парой (x₀; y₀) данная система автоматически будет иметь своим решением и пару (-x₀; y₀). Что при требовании единственности решения означает, что

Далее по проторенной дорожке — подставляем в нашу систему х = 0 и ищем необходимые значения параметра a:

Получили два необходимых значения параметра a. Необходимых для чего? Для того, чтобы пара чисел (0; y₀) была решением нашей системы. И не более того. Сколько этих решений окажется на самом деле, ещё непонятно. Что ж, снова тестируем наших кандидатов, подставляя каждого в исходную систему.)

Итак, проверяем a = 0.

Следующий клиент, a = 2.

Здесь уже так просто не выкрутиться (а я предупреждал, что проверка достаточности — очень часто самая сложная часть решения задач). В таких нестандартных ситуациях, когда в уравнении слева и справа стоят какие-то разнородные (и обычно ограниченные) конструкции (в нашем случае это модуль и косинус), чаще всего применяется метод оценок или, более научно и красиво, метод мажорант. Что ж попробуем оценить каждое из уравнений.

Ну, во-первых, про модуль мы знаем, что он всегда неотрицателен:

.

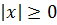
Значит, про левую часть первого уравнения можно сказать следующее:

.

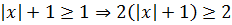
Итак, левая часть первого уравнения в любом случае не меньше двойки.

Что ещё в первом уравнении можно оценить? Ну, очевидно, косинус:

.

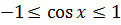
А вот всю правую часть первого уравнения мы пока оценить не можем: у нас ещё нет никакого ограничения на игрек. Ничего, сейчас получим.)

Для этого переключимся на второе уравнение:

Смотрим на него и прикидываем: слева стоит сумма квадратов — двух неотрицательных слагаемых. И эта сумма квадратов даёт единицу.

А теперь подумаем: какие такие два неотрицательных числа в сумме могут давать единицу? Как нетрудно догадаться, это могут быть либо какие-то дроби от нуля до единицы (например, 0,5 или 1/3), либо же когда одно из слагаемых равно в точности нулю, а другое — в точности единице. Значит, по-любому

0 ≤ sin 2 x ≤ 1 и 0 ≤ y 2 ≤ 1.

Итак, мы установили ограничения на косинус и на игрек. Они таковы:

А это значит, что их сумма (т.е. вся правая часть первого уравнения) ограничена вот так:

А теперь смотрим на первое уравнение системы

и на наши ограничения.

Для левой части: 2(|x|+1) ≥ 2, т.е. левая часть не меньше двойки.

Как вы думаете, когда возможно равенство обеих частей уравнения? Да! Когда каждая из них одновременно в точности равна двойке!

Значит, первое уравнение системы распадается на два условия:

Вместе со вторым уравнением системы получим:

Нетрудно убедиться (а это достаточно просто), что единственным решением этой системы (а значит, и исходной) является пара чисел (0; 1). Это значит, что значение параметра a = 2 нас полностью устраивает. Всё, задача полностью решена, можно записывать окончательный ответ.

Кстати, стандартный способ подстановки (размышления синим цветом в самом начале решения этого примера), который был нами прерван, здесь со скрипом, но тоже действует.) Кому интересно, попробуйте довести решение до конца, продолжив разложение на множители и приравняв каждый к нулю. 🙂 А вот следующий пример уже куда серьёзнее будет.

Пример 4

Уже при первом взгляде на систему видно, что ничего никуда не преобразуется, переменные друг через друга «красиво» не выражаются — ни y через x, ни x через y. Значит, стандартные приёмы не катят. Но! Переменная икс у нас снова везде стоит под модулем или в квадрате, т.е. под чётными функциями! А это означает, что единственным решением данной системы может быть только пара вида (0; y₀). Почему это именно так, объяснять, думаю, уже не нужно.) Если всё же непонятно, просмотрите ещё раз хотя бы предыдущий пример.

При подстановке x = 0 вся наша термоядерная система существенно упрощается:

Поехали, подставляем в систему a = 2/5. В этом случае вся система примет вид:

В первом уравнении я, во-первых, сократил двойки, а во-вторых, все члены с пятёркой собрал слева, а с тройкой — справа. Зачем — станет ясно ниже.)

Далее размышляем примерно так:

«Перед нами страшная система, которую как-то необходимо решить. Точнее не столько решить, сколько выяснить, сколько именно решений она имеет — единственное или нет. Или, возможно, вообще не имеет решений.) Но есть одна проблемка. Как к ней подступиться?

Если традиционно выразить y через x из второго уравнения, то будет

И что потом с этим плюс/минусом делать?! Непонятно…

А если выразить игрек из первого уравнения? Тогда вообще кошмар получится:

А если икс через игрек из второго? Тоже не фонтан. Значит, стандартные приёмы здесь явно не работают. Так… Но у нас в обоих уравнениях фигурируют модули и квадраты — ограниченные (снизу) конструкции. А что, если попробовать оценить левую и правую части первого (самого страшного) уравнения?»

Верные мысли! Итак, наша цель на данный момент – оценить обе части первого уравнения. Затяните потуже ремни на брюках, поскольку сейчас нам предстоит решать много неравенств. Точнее, не столько решать, сколько их выписывать, складывать, преобразовывать и т.д. Итак, перед оцениваем первое уравнение:

.

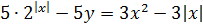
Но для начала обратим наш взор на второе уравнение:

Снова, как и в примере 3, видим сумму квадратов, равную единице. О чём это говорит? О том, что каждый из этих квадратов сам по себе не превосходит 1.

То же самое можно сказать и про модули икса и игрека:

Если теперь все три части последнего неравенства помножить на 5, то получим:

Теперь, сложив почленно эти два неравенства, получим ограничение на всю левую часть целиком:

Запомним этот факт.) Обратимся теперь к правой части уравнения: 3x 2 — 3|x|.

А вот её будем оценивать немного иначе.

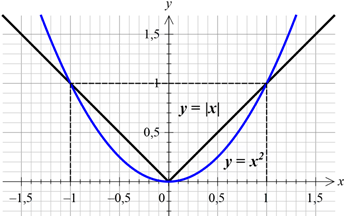
Далее воспользуемся одним весьма нетривиальным, но очень полезным сравнением:

Откуда я его взял? Как фокусник из рукава вытащил?)

Видно, что на отрезке [-1; 1] «уголок» везде, кроме точек 0 и ±1 лежит выше параболы.

Тогда x 2 — |x| ≤ 0 (я просто перенёс модуль влево).

Значит, если это неравенство умножить на 3, то получим:

Таким образом, вся правая часть не больше нуля.

А теперь вспоминаем, что же у нас с левой частью:

Таким образом, левая часть не меньше нуля.

Значит, равенство левой и правой частей возможно лишь в одном случае — когда каждая из них отдельно равна нулю:

Решаем эту системку.)

Отсюда легко получаем три пары: (0; 1), (-1; 2), (1; 2).

Однако, решения этой системы — это на самом деле лишь решения первого уравнения нашей глобальной системы.) Вспоминаем про её второе уравнение: x 2 + y 2 = 1.

Нетрудно убедиться, что из этих трёх пар ему удовлетворяет лишь пара (0; 1). А что это означает? В дебрях долгих выкладок и рассуждений, неволей, и про основной вопрос забываешь… ) Да! При a = 2/5 наша исходная система и вправду имеет единственное решение.

Всё, a = 2/5 обводим как часть ответа.)

А вот здесь так красиво провести оценку уже не получится: десятка справа всё испортила.( Как быть? В таких ситуациях, как правило, приходится прибегать к самой крайней мере — попытаться тупо подбором угадать два каких-нибудь решения и таким образом доказать, что система имеет более одного решения.) Как угадывать? Ну, тут уже всё от конкретного задания зависит. И немного от интуиции и иногда от везения. В нашем случае попробуем зацепиться за второе уравнение:

Что ещё можно проверить? Ха! У нас же симметрия по икс! Мы же как раз этот факт использовали для решения всей задачи! И думать не надо — тут же всплывает решение (-1; 0)!

Что ж, мы уже набрались достаточно опыта, чтобы рассмотреть какую-нибудь откровенную жесть. Берём быка за рога! 🙂

Пример 5

Ничего не боимся и стараемся при виде подобных монстров мыслить примерно следующим образом:

«Ух, наворотили, ужас! Корень, тангенс, синусы… Точно не решить… Так, стоп! От нас хотят найти единственное решение. Значит, скорее всего, нас просят отыскать какую-нибудь инвариантную конструкцию и с её помощью решить всю задачу.

Но есть ещё первое уравнение. В нём пока что никакой инвариантностью относительно перестановки икса и игрека и не пахнет. А вдруг, эту инвариантность и там удастся выявить? Ну-ка, посмотрим…

И что тут можно сделать? Можно хотя бы пораскрывать все скобки:

Вставляем всё в уравнение:

Ну, хорошо, а дальше? Сгруппируем-ка в кучку квадраты и первые степени. Хуже не будет. Будет либо хорошо, либо никак.)

Кажется, уже что-то вырисовывается:

Ну, вот и выявилось то, чего мы так добивались: x 2 +y 2 и x+y – инвариантные конструкции. Относительно замены x на y и y на x. Ура!»

Из второго уравнения сразу ясно, что х = 0. Третье уравнение при х = 0, очевидно, выполняется. А из первого уравнения при х = 0 получим:

Ух ты, как интересно! Получено одно единственное допустимое значение параметра. Минус два. Но радоваться рано, т.к. это ещё не ответ: нам же ещё достаточность надо проверить (да-да!). Деваться некуда, подставляем минус двойку в исходную систему вместо «а»:

По максимуму упрощаем каждое из уравнений. В первом раскроем все скобки:

Во втором уравнении благополучно обнуляется самое ужасное слагаемое с корнем, сокращается двойка, оставшаяся от первой скобки, и остаётся лишь

Ну, а третье уравнение так и оставим, без изменений. Итого:

А теперь делаем такой финт ушами — подставляем в первое уравнение вместо x + y выражение 2sin 2 z из второго. Что получим:

Проанализируем полученное уравнение. Чем оно примечательно? Тем, что слева стоит сумма каких-то квадратов, т.е. неотрицательных слагаемых! А когда возможно равенство нулю суммы неотрицательных слагаемых? Только в одном единственном случае — когда одновременно каждое слагаемое равно нулю! То есть:

Итак, единственным решением первого уравнения является тройка чисел (0; 0; 0). Проверим эту тройку и по остальным уравнениям: вдруг, она там не пройдёт? Тогда ответом, очевидно, будет пустое множество.)

Разумеется, эти рассмотренные пять примеров далеко не исчерпывают всего многообразия параметрических задач на единственное решение и инвариантность. ) Но в них я постарался максимально подробно и доходчиво изложить, как действовать в ситуации, если, вдруг, где-то (в пробнике или в настоящем ЕГЭ) вам попалась подобная задача. Итак, подытожим тему:

2) Выявив тип инвариантности, составляем необходимое условие единственности решения и ищем допустимые (необходимые) значения параметра. Как правило, вся задача при этом существенно упрощается, и их поиск не составляет особого труда.

3) Проверяем найденные допустимые значения параметра на достаточность . В случае, если получаемая задача не решается стандартными методами, применяем специальные приёмы — ограниченность, монотонность и т.п. Если и они не помогают — пробуем подобрать корень или решение. Чаще всего они лежат на поверхности и, как правило, являются целыми числами.

4) Не боимся. Пробуем различные варианты.) И побольше тренируемся.) Только так можно выработать необходимый опыт в решении таких (да и вообще любых) задач с параметрами.

Источник