Что значит равномерные шкалы
Reveal the Data
Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.
Равномерная шкала
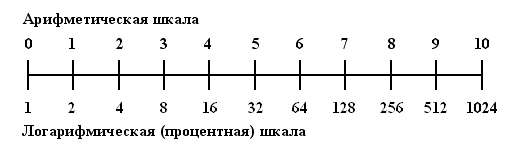
Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.
Логарифмическая шкала
Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.
Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.
Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.
Степенная шкала
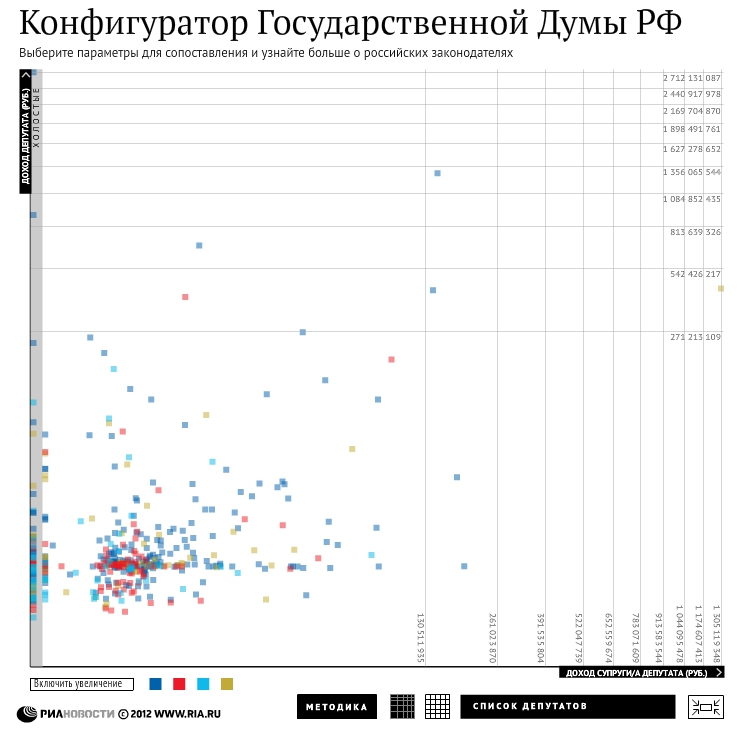
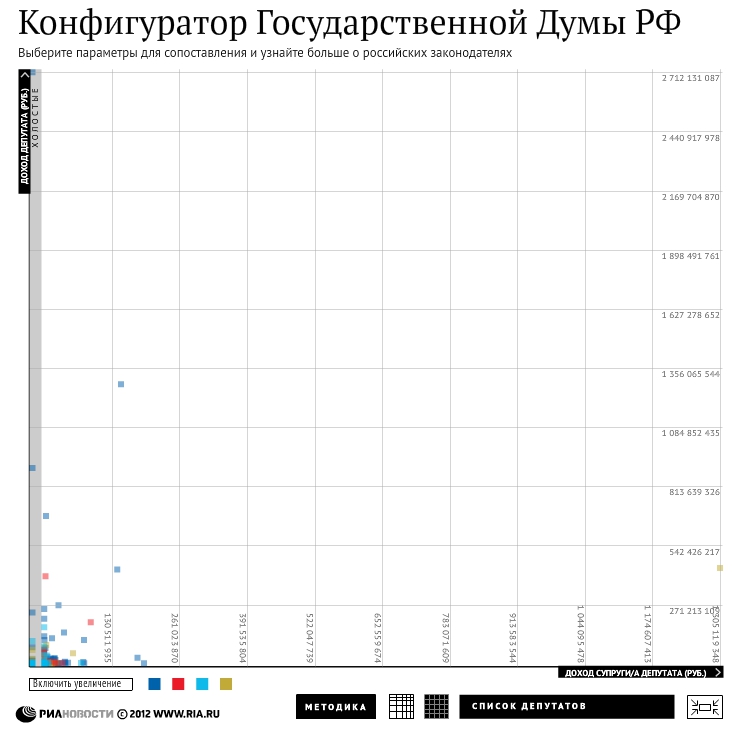
Это менее известный тип шкал. Он отличается от остальных тем, что расстояние между рисками, соответствует числам возведенным в степень. То есть получается, что расстояние между соседними рисками постоянно растёт или уменьшается. Такие шкалы удобны, когда мы хотим показать на одном графике более детально какую-то группу значений, но при это не хотим потерять из вида, значения которые, сильно отличаются от этой группы. Чем-то это похоже на логарифмическую шкалу, но здесь идёт акцент не на всем промежутке, а только на отдельной его части. Это хорошо видно на примере РИА новости, где они использовали степенные шкалы, чтобы сгладить выбросы по доходам отдельных депутатов.
Со степенной шкалой
С равномерной шкалой
То есть степенные шкалы используются когда данные смещены в ту или иную сторону.
Сравнение шкал
Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.
Что значит равномерные шкалы
Счётная линейка получила широкое применение в инженерных расчётах, а с повышением технического уровня нашей страны она становится необходимым инструментом не только инженера, но и квалифицированного рабочего.
Устройство счётной линейки основано на теории логарифмов, но для практического пользования линейкой можно обойтись без знания логарифмов.
Для того чтобы в совершенстве овладеть вычислениями на линейке, необходимо непрерывно упражняться и пользоваться ею при всевозможных расчётах на уроках математики, физики, химии, машиноведения, а также в мастерских и вне школы.
§ 85. Равномерные и неравномерные шкалы.
Рассмотрим обыкновенную миллиметровую линейку (черт. 34).
Если принять за единицу длины отрезок в 1 см, то в точке а (черт. 35) мы прочтём число 0,8, в точке
в точке 

Итак, в зависимости от того, какую длину мы принимаем за единицу, значение одного и того же штриха шкалы изменяется.
Так как один и тот же штрих шкалы может обозначать различные числа, отличающиеся друг от друга в 
При помощи двух равномерных шкал можно устроить прибор для сложения и вычитания чисел. На чертеже 36 показано, как на таком приборе найти сумму 14 и 26.
Для того чтобы осуществить это сложение, нужно против 14 на нижней шкале поставить 0 (начало) верхней шкалы, и тогда против 26 верхней шкалы прочтем на нижней
Легко сообразить, как на этом приборе, можно производить вычитание двух чисел.
Но если вместо равномерных шкал воспользоваться специальными неравномерными шкалами, то оказывается возможным производить умножение, деление, возведение в степень и другие действия над числами.
Познакомимся с некоторыми неравномерными шкалами.
На чертеже 37 изображена мерная коническая мензурка, которая кверху расширяется, и расстояния между делениями шкалы постепенно уменьшаются, хотя соответствующие им объёмы жидкости равны. На мензурке мы видим неравномерную шкалу.
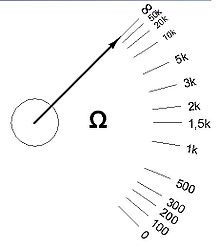
На многих электрических приборах можно увидеть неравномерные шкалы, например на амперметре (черт. 38), вольтметре и др. Дальше мы подробно рассмотрим неравномерные шкалы на счётной линейке.
Виды шкал средств измерений
Односторонняя шкала — шкала с нулевой отметкой, расположенной в начале или в конце шкалы
Двусторонняя шкала — шкала с нулевой отметкой, расположенной между начальной и конечной отметками.
Различают симметричные (начальная и конечная отметки соответствуют одинаковым значениям измеряемой величины) и несимметричные двусторонние шкалы (начальной и конечной отметкам соответствуют разные значения).
Рис. 8 Неравномерная шкала омметра
Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
Равномерная шкала — шкала, отметки на которой нанесены равномерно.
Стрелочные измерительные приборы: вольтметры, амперметры, омметры и т. д., обладают шкалами. Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка.
Отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.
Рис. 10 Многофункциональный прибор, Тестер
Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет, как правило, условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.
Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.
Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.
Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.
У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.
Рис. 12 Миллиамперметр
Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.
В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.
Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.
Рис. 13 Многофункциональный прибор, Тестер
На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.
Цена деления шкалы микроамперметра А1.
Микроамперметр А1 измеряет силу тока до 50 мкА. Шкала прибора содержит 5 больших делений, каждое из которых разделено еще на 10 делений.
Для того чтобы определить показание микроамперметра необходимо умножить цену деления на количество делений шкалы, соответствующих отклонению стрелки прибора.
Пример 1.Отклонение стрелки соответствует 2 большим или 20 маленьким делениям. Показание микроамперметра равно 10мкА * 2 = 20 мкА или 1мкА * 20 = 20 мкА.
Измерение. Шкалы измерений
Известное изречение гласит «все познается в сравнении».
Для идентификации объектов и их характеристик во множестве их проявлений требуется большое количество и разнообразие мер. С учетом особенностей измеряемых объектов и задач измерений меры группируют и используют для построения шкал измерений.
Шкала измерений – упорядоченное множество проявлений количественных или качественных характеристик объектов, а также самих объектов. Указанное множество может быть образовано из наименований и обозначений (в том числе в цифровой форме) объектов и их характеристик, а также из значений и числовых значений (для количественных характеристик).
Согласно РМГ 83-2007 [7] «шкала измерений – отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений)». «Измерение – сравнение конкретного проявления измеряемого свойства (величины) со шкалой измерений этого свойства (величины) в целях получения результата измерений (оценки свойства или значения величины)».
Под качественной характеристикой в определении шкалы измерений и далее понимается описание объектов, их свойств и состояний, в словесной форме, в том числе с использованием наименований и обозначений.
Количественная характеристика – характеристика, которая может быть представлена числовым значением, равным отношению количественного содержания этой характеристики к еѐ базовой реализации, называемой единицей измерения.
Шкала наименований – шкала, состоящая из множества наименований (обозначений) объектов или проявлений их характеристик, в соответствии которым поставлено описание объекта (конкретная реализация объекта, его графическое изображение, математическая формула, график и т.п.) или проявлений его характеристик.
Наименование (обозначение) в этом случае рассматривают как обобщенную характеристику объекта или его свойств и состояний. С помощью шкалы наименований устанавливают эквивалентность (равноценность) измеряемого объекта или его характеристик и описания, поставленному в соответствие тому или иному наименованию (обозначению). Это позволяет отнести объект к какой-либо группе или выделить его, путем присвоения индивидуального наименования (обозначения), после чего наименования (обозначения) применяются как идентификаторы объектов (характеристик объектов). При построении шкал наименований могут использоваться числа, но лишь как метки объектов. Примерами таких шкал являются: атласы цветов (до 1000 наименований), запахов (сырой, затхлый, кислый и т.д.), вкуса (чистый, полный, гармоничный и т.д.); множество номеров телефонов, автомашин, паспортов; разделение людей по полу, расе, национальности; классификаторы промышленной продукции, специальностей высшего образования; терминологические справочники и т.п.
Числа, знаки, обозначения, наименования, составляющие шкалу наименований, разрешается менять местами. Для результатов измерений, полученных с использованием этой шкалы, нет отношений типа «больше — меньше», не применимы понятия единица измерения, нуль, размерность. С ними могут проводиться только некоторые математические операции. Например, числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Оценки экспертов часто осуществляются с использованием шкал порядка. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию.
В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п. Однако нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
Шкалы наименований и порядка, для которых не определены единицы измерений, называют также условными шкалами или не метрическими шкалами.
Абсолютная шкала – шкала числовых значений количественной характеристики. Отличительные признаки абсолютных шкал: наличие естественного нуля и отсутствие необходимости в единице измерений. С использованием абсолютных шкал измеряют коэффициенты усиления, ослабления, амплитудной модуляции, нелинейных искажений, отражения, коэффициент полезного действия и т. п. Результаты измерений в абсолютных шкалах при необходимости выражают в процентах, промилле, байтах, битах, децибелах.
Разновидностью абсолютных шкал являются дискретные (счетные) шкалы, в которых результат измерения выражается числом частиц, квантов, или других объектов, эквивалентных по проявлению измеряемого свойства. Например, шкалы для электрического заряда ядер атомов, числа квантов (в фотохимии), количества информации. Иногда за единицу измерений (со специальным названием) в таких шкалах принимают какое-то определенное число частиц (квантов), например один моль – число частиц, равное числу Авогадро.
Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы) называют абсолютной ограниченной шкалой.
Шкалы разностей (интервалов), отношений и абсолютные классифицируют как метрические или физические шкалы. Эти шкалы допускают логарифмическое преобразование, часто применяемое на практике, что приводит к изменению типа шкал. Такие шкалы называют логарифмическими. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.
Практически реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, при необходимости, способов и условий (спецификаций) их однозначного воспроизведения.
Измерение с помощью шкал заключается в установлении соответствия объекта или его характеристики отметке на шкале измерений. После чего объекту измерений приписывают количественную или качественную определенность, соответствующую выявленной отметке шкалы.
Большая Энциклопедия Нефти и Газа
Равномерная шкала
Равномерные шкалы имеют одинаковый размер всех делений. У неравномерных шкал размер каждого последующего деления уменьшается или увеличивается с определенной закономерностью, зависящей от принципа преобразования измеряемой величины. [1]
Равномерные шкалы ( например, для образцовых манометров) обычно рассчитывают и изготовляют без предварительной градуировки. После установки такой шкалы на прибор достаточно отрегулировать измерительный механизм или схему таким образом, чтобы крайние отметки совпадали с соответствующими значениями измеряемой величины. Все остальные отметки должны после этого иметь правильное значение без какой-либо дополнительной регулировки. [3]
Равномерные шкалы имеют одинаковый размер всех делений. У неравномерных шкал размер каждого последующего деления уменьшается или увеличивается с определенной закономерностью, зависящей от принципа преобразования измеряемой величины. [4]
Равномерные шкалы ( например, для образцовых манометров) обычно рассчитывают и изготовляют без предварительной градуировки. После установки такой шкалы на прибор достаточно отрегулировать измерительный механизм или схему таким образом, чтобы крайние отметки совпадали с соответствующими значениями измеряемой величины. Все остальные отметки должны после этого иметь правильное значение без какой-либо дополнительной регулировки. [6]
Равномерные шкалы имеют одинаковый размер всех делений. У неравномерных шкал размер каждого последующего деления уменьшается или увеличивается с определенной закономерностью, зависящей от принципа преобразования измеряемой величины. [7]
Равномерные шкалы ( например, для образцовых манометров) обычно рассчитывают и изготовляют без предварительной градуировки. После установки такой шкалы на прибор достаточно отрегулировать измерительный механизм или схему таким образом, чтобы крайние отметки совпадали с соответствующими значениями измеряемой величины. Все остальные отметки должны после этого иметь правильное значение без какой-либо дополнительной регулировки. [9]
Равномерная шкала фиксированных направлений обусловливает неравномерное квантование этих приращений. [11]
Равномерную шкалу прибора можно также получить, используя мембранную коробку с линейной характеристикой и передаточный механизм, при котором угол поворота стрелки был бы пропорционален корню квадратному из смещения центра коробки. [12]
Равномерной шкале квантования координатных приращений соответствует неравномерная система фиксированных направлений. [14]
Построение равномерной шкалы производится следующим образом. [15]