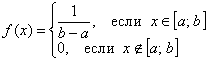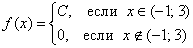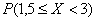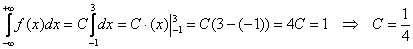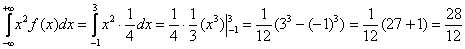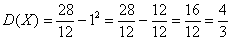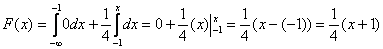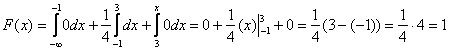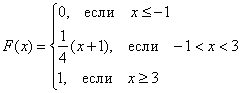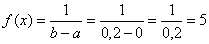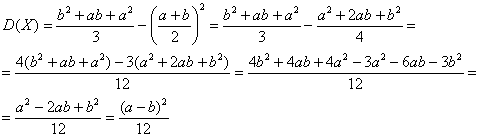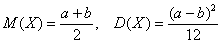Что значит равномерное распределение
Что значит равномерное распределение
13.5.3 тБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ
оБ РТБЛФЙЛЕ ЬФП ТБУРТЕДЕМЕОЙЕ ЧУФТЕЮБЕФУС ФПЗДБ, ЛПЗДБ УТЕДЙ РТЙОЙНБЕНЩИ УМХЮБКОЩНЙ ЧЕМЙЮЙОБНЙ ЪОБЮЕОЙК ОЕФ ЛБЛЙИ МЙВП РТЕДРПЮФЙФЕМШОЩИ. ч ЮБУФОПУФЙ, ПВЩЮОП УЮЙФБАФ, ЮФП УПВЩФЙС, РТПЙУИПДСЭЙЕ Ч РТПЙЪЧПМШОЩЕ НПНЕОФЩ ЧТЕНЕОЙ У ТБЧОПК ЧЕТПСФОПУФША НПЗХФ РТПЙУИПДЙФШ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ.
 |  |
| тЙУ 1. | тЙУ 2. |
оБКДЕН ЪОБЮЕОЙЕ РПУФПСООПК у ЙЪ ХУМПЧЙС, ЮФП РМПЭБДШ, ПЗТБОЙЮЕООБС ЛТЙЧПК ТБУРТЕДЕМЕОЙС, ТБЧОБ ЕДЙОЙГЕ.

пФУАДБ 
оБКДЕН ЧЩТБЦЕОЙЕ ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС F(И) ДМС ТБЧОПНЕТОПЗП ЪБЛПОБ ТБУРТЕДЕМЕОЙС
фБЛЙН ПВТБЪПН, ЙНЕЕН
зТБЖЙЛ ЖХОЛГЙЙ F(x) ЙЪПВТБЦЕО ОБ ТЙУХОЛЕ 2.
пРТЕДЕМЙН ПУОПЧОЩЕ ЮЙУМПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ УМХЮБКОПК ЧЕМЙЮЙОЩ и, ЙНЕАЭЕК ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ.

йФБЛ, НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ ТБЧОПНЕТОПЗП ТБУРТЕДЕМЕОЙС ОБИПДЙФУС РПУЕТЕДЙОЕ ЙОФЕТЧБМБ 

нПДЩ ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ ОЕ ЙНЕЕФ.
дЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ и ОБИПДЙН РП ЖПТНХМЕ
фП ЕУФШ 

чЕТПСФОПУФШ РПРБДБОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ и, ЙНЕАЭЕК ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ, ОБ ПФТЕЪПЛ 

Равномерное распределение вероятностей
Простейшее из непрерывных распределений, с помощью которого моделируются многие реальные процессы. И самый такой распространённый пример – это график движения общественного транспорта. Предположим, что некий автобус (троллейбус / трамвай) ходит с интервалом в 10 минут, и вы в случайный момент времени подошли к остановке. Какова вероятность того, что автобус подойдёт в течение 1 минуты? Очевидно, 1/10-я. А вероятность того, что придётся ждать 4-5 минут? Тоже 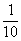
Рассмотрим некоторый конечный промежуток, пусть для определённости это будет отрезок 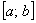
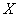
И в самом деле, если длина отрезка (см. чертёж) составляет 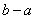
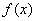
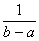
Проверим его формально: 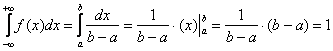
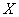
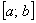
Суть равномерности состоит в том, что какой бы внутренний промежуток фиксированной длины 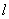
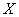
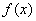
Рассмотрим типовое задание:
Непрерывная случайная величина 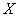
Найти константу 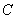
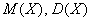
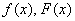
Иными словами, всё, о чём только можно было мечтать 🙂
Решение: так как на интервале 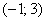
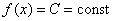
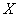
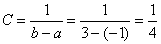
…почему лучше? Чтобы не было лишних вопросов 😉
Таким образом, функция плотности:
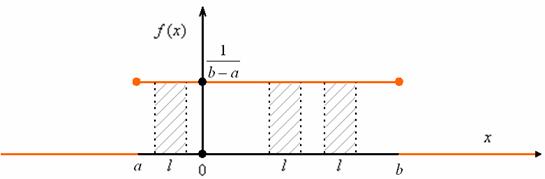
Выполним чертёж. Значения 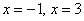
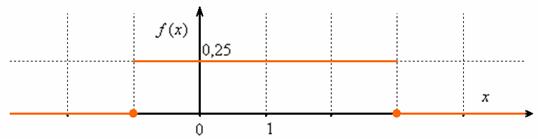
В качестве экспресс-проверки вычислим площадь прямоугольника: 
Найдём математическое ожидание, и, наверное, вы уже догадываетесь, чему оно равно. Вспоминаем «10-минутный» автобус: если случайным образом подходить к остановке много-много дней упаси, то в среднем его придётся ждать 5 минут.
Да, именно так – матожидание должно находиться ровно посерединке «событийного» промежутка: 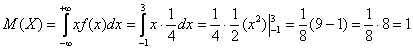
Дисперсию вычислим по формуле 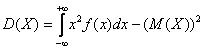
Таким образом, дисперсия:
Составим функцию распределения 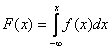
1) если 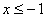
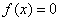
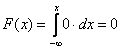
2) если 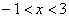
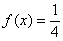
3) и, наконец, при 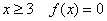
В результате:
Выполним чертёж: 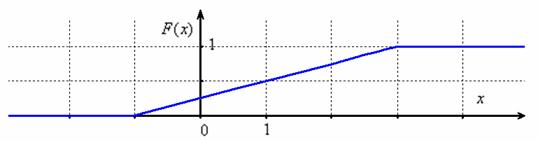
На «живом» промежутке функция распределения растёт линейно, и это ещё один признак, что перед нами равномерно распределённая случайная величина. Ну, ещё бы, ведь производная линейной функции – есть константа.
Требуемую вероятность можно вычислить двумя способами, с помощью найденной функции распределения: 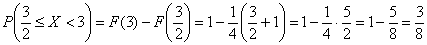
либо с помощью определённого интеграла от плотности: 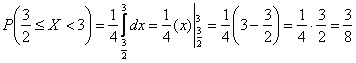
Кому как нравится.
И здесь ещё можно записать ответ: 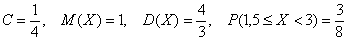
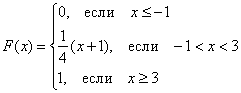
…«можно», потому что за его отсутствие обычно не карают. Обычно 😉
Для вычисления 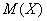
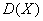
Непрерывная случайная величина 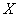
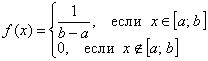
Вычислить математическое ожидание и дисперсию. Результаты максимально упростить (формулы сокращённого умножения в помощь).
Полученные формулы удобно использовать для проверки, в частности, проверьте только что прорешанную задачу, подставив в них конкретные значения «а» и «б». Краткое решение внизу страницы.
И в заключение урока мы разберём парочку «текстовых» задач:
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Считая, что погрешности округлений распределены равномерно, найти вероятность того, что при очередном измерении она не превзойдёт 0,04.
Для лучшего понимания решения представим, что это какой-нибудь механический прибор со стрелкой, например, весы с ценой деления 0,2 кг, и нам предстоит взвесить кота в мешке. Но не в целях выяснить его упитанность – сейчас будет важно, ГДЕ между двумя соседними делениями остановится стрелка.
Рассмотрим случайную величину 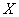
Составим функцию плотности распределения вероятностей:
1) Так как расстояние не может быть отрицательным, то на интервале 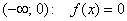
2) Из условия следует, что стрелка весов с равной вероятностью может остановиться в любом месте между делениями*, включая сами деления, и поэтому на промежутке 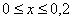
* Это существенное условие. Так, например, при взвешивании кусков ваты или килограммовых пачек соли равномерность будет соблюдаться на куда более узких промежутках.
3) И поскольку расстояние от БЛИЖАЙШЕГО левого деления не может быть больше, чем 0,2, то при 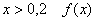
Таким образом:
Следует отметить, что о функции плотности нас никто не спрашивал, и её полное построения я привёл исключительно в познавательных цепях. При чистовом оформлении задачи достаточно записать только 2-й пункт.
Теперь ответим на вопрос задачи. Когда погрешность округления до ближайшего деления не превзойдёт 0,04? Это произойдёт тогда, когда стрелка остановится не далее чем на 0,04 от левого деления справа или не далее чем на 0,04 от правого деления слева. На чертеже я заштриховал соответствующие площади: 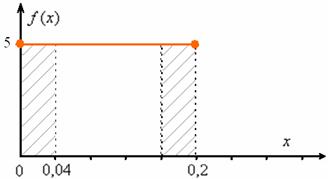
Осталось найти эти площади с помощью интегралов. В принципе, их можно вычислить и «по-школьному» (как площади прямоугольников), но простота не всегда находит понимание 😉
По теореме сложения вероятностей несовместных событий: 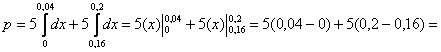
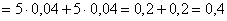
Легко понять, что максимально возможная погрешность округления составляет 0,1 (100 грамм) и поэтому вероятность того, что ошибка округления не превзойдёт 0,1 равна единице. И из этого, кстати, следует другой, более лёгкий способ решения, в котором нужно рассмотреть случайную величину 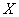
Ответ: 0,4
И ещё один момент по задаче. В условии речь может идти о погрешностях не округлений, а о случайных погрешностях самих измерений, которые, как правило (но не всегда), распределены по нормальному закону. Таким образом, всего лишь одно слово может в корне изменить решение! Будьте начеку и вникайте в смысл задач!
И коль скоро всё идёт по кругу, то ноги нас приносят на ту же остановку:
Автобусы некоторого маршрута идут строго по расписанию и интервалом 7 минут. Составить функцию плотности случайной величины 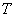
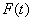
Несмотря на то, что время не может быть отрицательным, интервал 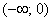
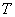
Краткое решение и ответ в конце урока. Дополнительные задачи с равномерным распределением можно найти в тематическом решебнике.
И не успел никто опомниться, как подошёл очередной автобус, который отвезёт нас до остановки Показательное распределение и конечной под названием Нормальное распределение вероятностей.
Пример 2. Решение: вычислим математическое ожидание: 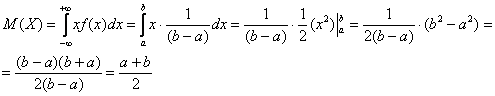
Дисперсию вычислим по формуле 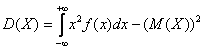
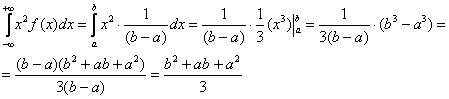
Таким образом:
Ответ:
Пример 4. Решение: случайная величина 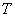
Вычислим вероятность того, что пассажир будет ожидать автобус не более 3 минут: 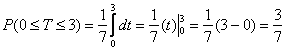
Составим функцию распределения 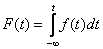
1) если 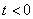
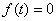
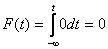
2) если 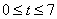
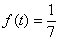
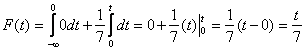
3) если 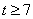
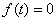
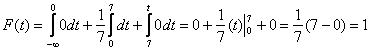
Таким образом: 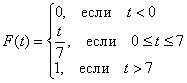
Функция 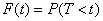
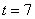
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5