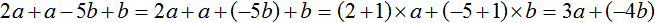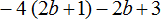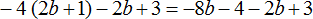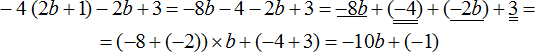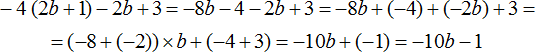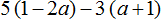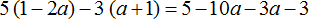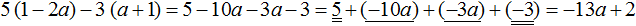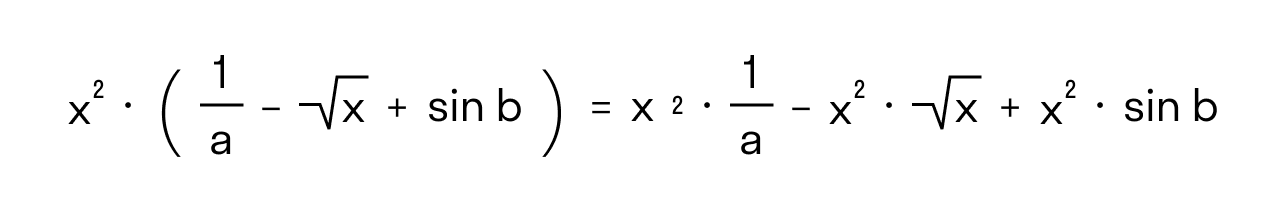Что значит раскройте скобки и приведите подобные слагаемые

6.4.2. Раскрытие скобок. Приведение подобных слагаемых

1. Раскрытие скобок, перед которыми стоит знак «+» или не стоит никакого знака.

Если перед скобками стоит знак «+» или не стоит никакого знака, то убираем скобки, знак «+» и записываем слагаемые, стоявшие в скобках, без изменений.

Примеры. Раскрыть скобки.

1в) 7x+(-a-2b+5c-k) = 7x-a-2b+5c-k.

2. Раскрытие скобок, перед которыми стоит знак «-».

Если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.

Примеры. Раскрыть скобки.

Числовой множитель, стоящий перед буквенным множителем, называют коэффициентом. Так, в выражении 5а коэффициент равен 5, а в выражении (-а) коэффициент равен (-1).

Нахождение алгебраической суммы подобных слагаемых называется приведением подобных слагаемых.

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).

Примеры. Привести подобные слагаемые.

3в) 5,2с-2,8с-6,4с+9с = (5,2-2,8-6,4+9)с = 5с.

4. В алгебраическом выражении могут быть различного вида подобные слагаемые. В этом случае подобные слагаемые подчеркиваются одинаковыми линиями.

Примеры. Привести подобные слагаемые.

5. Для преобразования алгебраических выражений с помощью раскрытия скобок используют распределительное свойство умножения: чтобы сумму чисел умножить на третье число, можно каждое слагаемое умножить на третье число и сложить результаты.

Примеры. Раскрыть скобки.

5а) 2 (4х-5у) = 2 ∙ 4х+2 ∙ (-5) = 8х-10у;

6. Упростить алгебраическое выражение – это значит раскрыть скобки, выполнить указанные действия, привести подобные слагаемые.

Примеры. Упростить выражение.

7. Примеры для самостоятельного решения. Упростить:

Источник

Раскрытие скобок

Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.

Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.

Первое правило раскрытия скобок

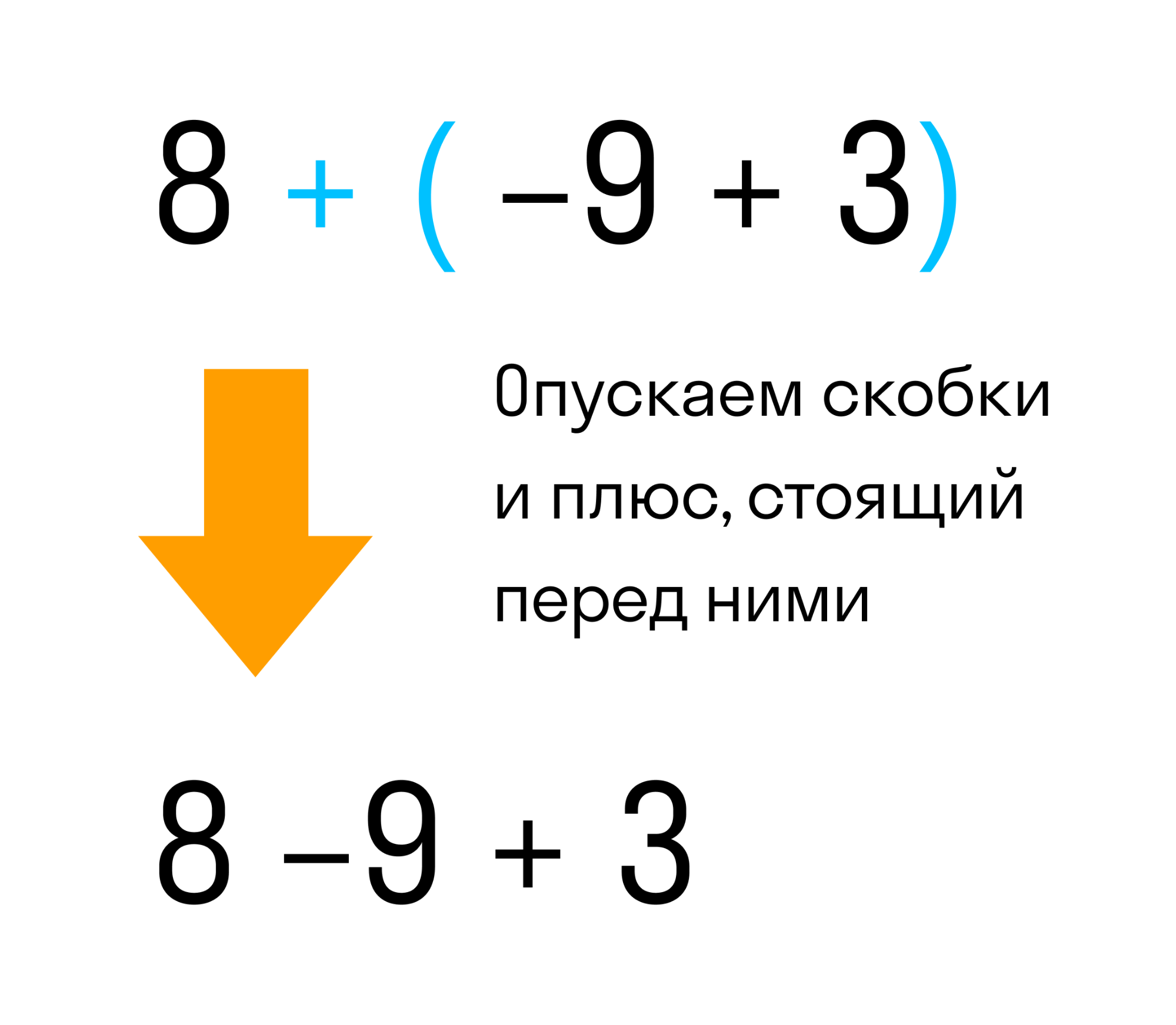
Рассмотрим следующее выражение:

Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.

Первое правило раскрытия скобок выглядит следующим образом:

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

Пример 3. Раскрыть скобки в выражении 2 + (−1)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.

Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:

Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)

В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:

Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)

Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:

Пример 5. Раскрыть скобки в выражении (−5)

Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)

Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)

В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Второе правило раскрытия скобок

Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

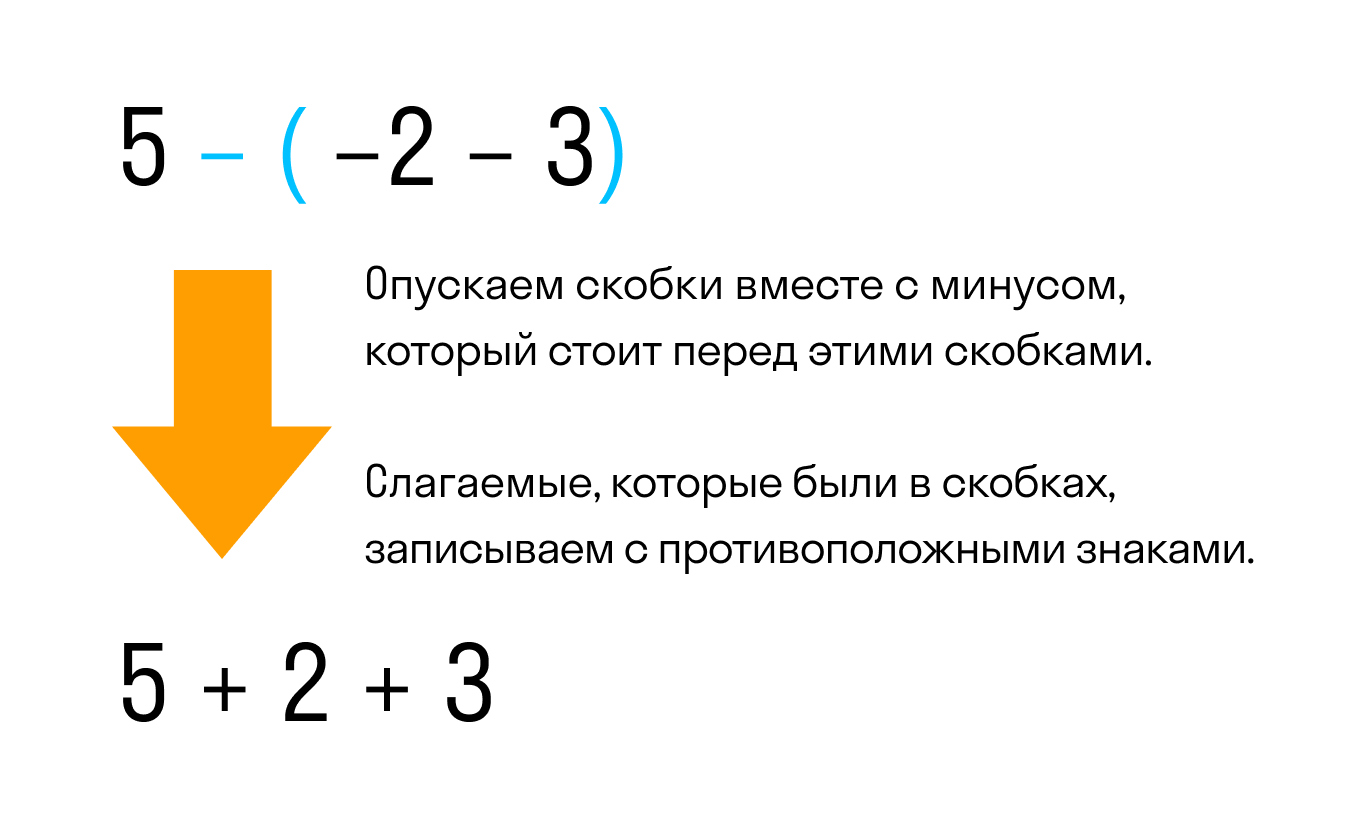
Например, раскроем скобки в следующем выражении

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:

Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 4. Раскрыть скобки в выражении −(−3 + 4)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:

−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2

Пример 6. Раскрыть скобки в выражении −(−a − 1)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 7. Раскрыть скобки в выражении −(4a + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:

2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5

Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)

Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:

−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15

Механизм раскрытия скобок

Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:

На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)

3 × (4 + 5) = 3 × 4 + 3 × 5

Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.

Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?

Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:

Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.

Для удобства заменим разность, находящуюся в скобках на сумму:

Далее умножаем общий множитель −1 на каждое слагаемое в скобках:

Но не мешает знать, как эти правила работают.

В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:

Раскрыть скобки и привести подобные слагаемые в следующем выражении:

Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:

1) Раскрываем скобки:

2) Приводим подобные слагаемые:

В получившемся выражении −10b+(−1) можно раскрыть скобки:

Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:

1) Раскроем скобки:

2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть

Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4

m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44

Источник

Подобные слагаемые, их приведение, примеры

Приведение подобных слагаемых является одним из наиболее употребимых тождественных преобразований. В этом разделе мы дадим определение термина, разберем, что обозначает словосочетание «приведение подобных слагаемых», рассмотрим основные правила выполнения действий и наиболее распространенные типы задач.

Определение и примеры подобных слагаемых

В большинстве учебных пособий тема подобных слагаемых разбирается после знакомства с буквенными выражениями, когда появляется необходимость проводить с ними различные преобразования.

Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.

Слагаемые – это, как известно, составные элементы суммы. Это значит, что они могут присутствовать лишь в тех выражениях, которые представляют собой сумму. Буквенная часть – это одна или произведение нескольких букв, которые представляют собой переменные. Слагаемые с буквенной частью – это произведение некоторого числа и буквенной части. Здесь некоторое число также носит название числового коэффициента.

Буквенная часть может быть представлена не только произведением букв, но также и произвольным буквенным выражением. Например:

Обобщим изложенные выше утверждения и дадим еще одно определение подобных слагаемых.

Подобные слагаемые – это слагаемые в буквенном выражении, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части, если под буквенной частью понимать любое буквенное выражение.

Числовые коэффициенты подобных слагаемых могут быть равны, тогда мы говорим о том, что подобные слагаемые одинаковые. Если же числовые коэффициенты различаются, то подобные слагаемые будут разными.

Возьмем для примера выражение 2 · x · y + 3 · y · x и рассмотрим такой нюанс: являются ли слагаемые 2 · x · y и 3 · y · x подобными. В задачах этот вопрос может иметь следующую формулировку: одинаково ли буквенное выражение части x · y и y · x указанных слагаемых? Буквенные множители в приведенном примере имеют различный порядок, что в свете данного выше определения не делает их подобными.

К слову, в некоторых источниках при нестрогом отношении к вопросу, слагаемые из примера могут называться подобными. Но лучше не допускать таких неточностей в трактовках.

Приведение подобных слагаемых, правило, примеры

Под преобразованием выражений, которые содержат подобные слагаемые, подразумевается проведение сложения этих слагаемых. Проводится это действие обычно в три этапа:

Приведем пример таких вычислений.

Описанные три шага для экономии времени записывают в виде правила приведения подобных слагаемых. Согласно правило для того, чтобы привести подобные слагаемые, необходимо сложить их коэффициенты, а затем умножить полученный результат на буквенную часть при ее наличии.

Решение

Источник

Раскрытие скобок

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

Первое правило раскрытия скобок

Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 18 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

Раскрытие круглых скобок при умножении одночлена на многочлен

Раскрытие круглых скобок при умножении многочлена на многочлен

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

Чтобы успешно решать подобные задания, нужно:

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

Теперь раскроем вторую скобку, внешнюю:

Упростим получившееся выражение:

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

Пример 1. Раскрыть скобки и упростить выражение:

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Источник