Что значит простые числа и составные числа
Простые и составные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Натуральные числа больше единицы бывают простые и составные.
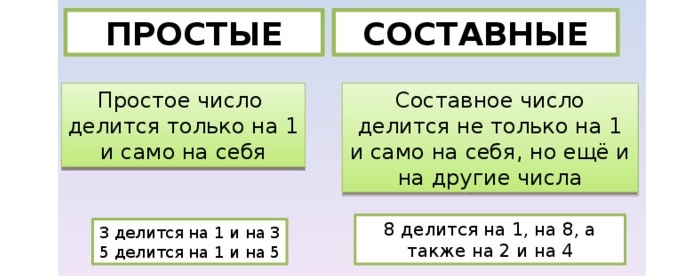
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
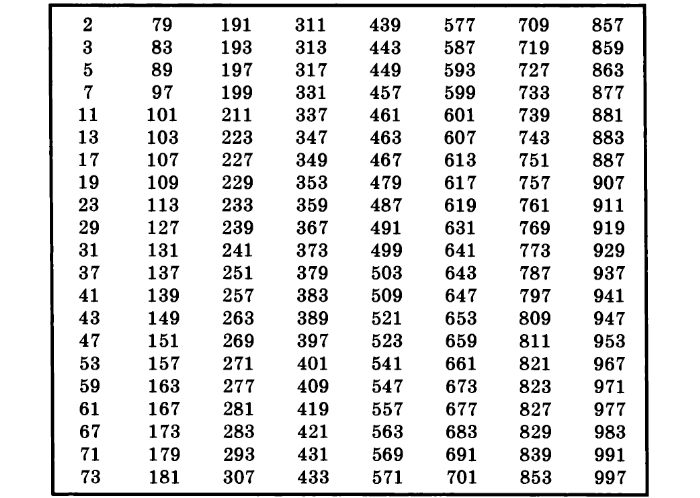
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.
Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами.
Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.
Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе.
Проверка на принадлежность к определенному множеству достаточно простая:
Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.
Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.
Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.
Простые двузначные числа определяются по внешнему виду:
Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.
Если на конце находится цифра 5, то она входит в число делителей.
Такие простые способы помогают легко классифицировать многозначные показатели.
Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.
Последовательность простых чисел
Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение.
Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше.
Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.
Наименьшее и наибольшее простое число
Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель.
Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.
Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу.
При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.
В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2 82 589 933
Множество простых чисел
Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.
Для изучаемых объектов к ним относятся:
принадлежность к натуральным;
наличие максимум двух делителей.
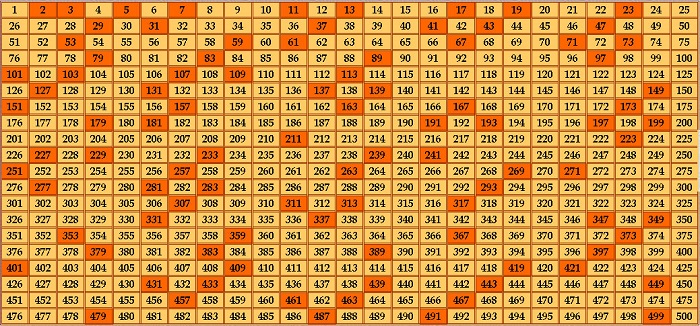
Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.
Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.
По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.
В итоге, все составные окажутся зачеркнутыми.
Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.
Некоторые свойства простых чисел
Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время.
Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.
Известны следующие правила:
Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.
Все являются нечетными, за исключением двойки.
Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.
Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.
Если одно из двух N делится на n, то их произведение также будет делиться на него.
Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.
Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.
Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.
Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.
Действия с простыми числами
Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени.
Извлечь корень из них невозможно.
Таблица простых чисел до 1000
Таблица простых числе до 10000
Простые и составные числа: определения и примеры
Простые и составные числа: Freepick
Математика по-разному называет числа и делит их на определенные группы. На уроках услышите о простых и составных числах. Чем обосновано такое деление и как научиться различать эти категории чисел? Помогут разобраться в этом вопросе примеры.
Простые числа и их особенности
Сложение, вычитание, умножение, деление — все эти операции привычны для математиков, которые ловко оперируют самыми разными числами и способны вести подсчеты в уме не хуже, чем вычислительные машины. Помогают им в этом простые и составные числа.
Познакомимся с первой группой чисел. Простое число — это любое число, которое можно разделить само на себя и на единицу. Яркий и простой для запоминания пример — число 13. Легко заключить, что разделить его получится:
Любое число, которому подходит под это определение, попадает в группу простых. Следует помнить о том, что подразумевается деление числа нацело. С целым или дробным остатком деление возможно практически для любых чисел.
Числа в математике: Freepick
Для удобства в математике используются таблицы простых чисел. При их составлении вручную последовательно проверяется каждое число. Например:
Такие операции можно выполнять до числа 100 и далее.
Но в книге о простых числах выдающегося математика Л. Г. Шнирельмана указано, что существует бесконечное множество простых чисел. Как быть и можно ли ускорить процесс их нахождения?
Математики нашли решение этой задачи. Быстро отобрать простые числа можно с помощью решета Эратосфена:
На уроках часто пользуются уже готовыми таблицами, но важно помнить о том, каким образом в них оказываются те или иные числа. Кроме простых, выделяют также группу взаимно простых чисел, у которых есть только один общий делитель — единица (например, 14 и 25).
Что такое составные числа
Количество составных чисел в разы превышает количество простых. Составными числами называют такие, которые не относятся к простым, то есть имеют делители, кроме единицы и самого себя. Иногда составные числа называют сложными.
Рассмотрим это на примере:
Таким образом, составным числом называют такое число, у которого есть два и более простых множителей.
Зачем математики используют простые и составные числа? Это необходимо для упрощения разложения на множители. Вместо долгих поисков того, на какие числа можно разложить большое значение, достаточно использовать специальную таблицу.
Разложение на простые множители необходимо для определения самого большого общего делителя и самого маленького общего кратного. Эти значения применяют в сложении, вычитании и сравнении дробей.
Математические расчеты: Freepick
Обсуждая простые и составные числа, не было сказано, в какую группу отнести ноль и единицу. Остановимся на единице. Согласно определению, у простого числа должно быть два делителя — единица и оно само.
Но для единицы делитель фактически один, потому к простым числам ее нельзя отнести. Составным числом единица также не может быть (нет более двух делителей), а потому она остается числом без категории.
Как быть с нулем? Ноль, в отличие от единицы, делится на любые числа и получается при этом все тот же ноль. Кроме того, его не получится разложить на простые множители. С учетом теории и определения простых и составных чисел математики приняли решение ноль, как и единицу, исключить из категорий простых и составных чисел.
Таким образом, математикам удалось классифицировать и разделить на две большие группы все многообразие чисел. Ученые сделали это, найдя для них общие признаки. Простые числа имеют только два делителя, а у составных их гораздо больше. Вне этой классификации остались лишь единица и ноль.
Уникальная подборка новостей от нашего шеф-редактора
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Простые числа
Простые числа намного полезнее, чем вы можете подумать, полагая их чисто умозрительными конструктами.
Простые числа — те числа, которые делятся без остатка только на само себя и 1. Это означает, что простое число нельзя представить в виде произведения (состоящего только из целых положительных чисел), кроме как:
[простое число] х 1 = [простое число]
Простые и составные
Составные числа — это числа, у которых есть делители, кроме самих себя и 1. Таким образом, все целые положительные числа, кроме 0 и 1, — либо простые, либо составные. Любое составное число можно представить в виде произведения простых сомножителей, то есть его можно разложить на множители, включающие только простые числа. Это наводит на мысль о важности простых чисел: это первичные блоки, из которых можно построить все остальные числа. Распределение простых чисел Теорема о распределении простых чисел, доказанная в XIX в., утверждает, что вероятность того, что случайным образом выбранное число n — простое, везде пропорциональна количеству цифр в нем, или логарифму n. Это означает, что чем больше число, тем меньше вероятность того, что оно будет простым.
Средний интервал между следующими друг за другом простыми числами к n приблизительно равен логарифму n, или ln(n).
Найти простое
Один из способов определения простого числа — «тест простоты». Если n — исследуемое число, то нужно попробовать разделить его на все числа больше 1 и меньше 1/2 n.
Самое большое обнаруженное простое число (на апрель 2015) содержит 17 425 170 знаков, это 2 57 885 161 – 1. Не стоит засиживаться до ночи, пытаясь выяснить следующее, если только вы не специализируетесь на этом, однако Фонд электронных рубежей (Electronic Frontier Foundation) назначил премию за первое простое число минимум в 100 миллионов знаков, а также за первое простое число минимум в пол миллиарда знаков.
Величайшие математические умы, а теперь еще и самые сложные компьютерные программы, давно пытаются найти закономерности в простых числах, но никакой предсказуемой закономерности до сих пор не было обнаружено.
Решето Эратосфена
Древнегреческий математик Евклид Александрийский, живший во II или III вв. до н. э., известен нам как первый человек, который выделил простые числа. Другой древнегреческий математик Эратосфен, II в. до н. э., представил свое так называемое «решето» для установления простых чисел. Оно годится только для относительно малых чисел, но его просто использовать.
Нарисуйте таблицу с 10 колонками и столькими рядами, сколько вам нужно, чтобы вместить числа, которые вы хотите проверить: если вы хотите проверить числа до n, нужно сделать таблицу от 1 до n. Начиная с 4, продвигайтесь по таблице и вычеркивайте все, что делится на 2. Затем вычеркните все, что делится на 3, затем — на 5, затем — на 7 и т. д., прокладывая путь сквозь простые числа. Когда вы доберетесь до делителя 1/2 n – 1, можете остановиться, так как большие числа не могут быть делителем n или меньших чисел. Числа, которые не были зачеркнуты, — простые.
Прискорбное пренебрежение
После Древней Греции и вплоть до XVII в. в интерес к простым числам почти отсутствовал. Даже в XVII в., простые числа не использовались нигде, кроме как в чистой математике, но ими, по крайней мере, стало позволительно поиграть. Они заняли свое законное место в компьютерную эпоху, с появлением необходимости в разработке шифровальных алгоритмов.
Есть работа
Простые числа пребывали в ленивом бездействии, пока не пришла необходимость в шифровании данных. Сейчас мы ежедневно посылаем несметное количество защищенных транзакций и других секретных данных через интернет, а простые числа предоставляют аналог защищенных фургонов, в которых перевозят данные. Начнем, перемножив два очень больших простых числа, чтобы получить составное число:
Составное число используется для генерации кода, который называется открытый ключ, который банк (или кто-нибудь) посылает человеку, желающему зашифровать свои данные. Если вы покупаете что-нибудь онлайн, данные вашей кредитки должны быть зашифрованы с использованием этого публичного ключа, шифрование происходит на вашем конце связи. Зашифрованные данные окажутся пустым набор слов, если будут перехвачены в процессе передачи. Когда данные вашей карты прибывают на другой конец, закрытый ключ — созданный из Р1 и Р2 — используется для расшифровки.
Это работает, так как очень сложно найти простые числа, из которых было получено составное, когда речь идет о больших числах. Любому хакеру понадобится 1000 лет компьютерного времени, чтобы взломать код и найти первоначальные простые числа. Именно потому, что так сложно взломать современный шифр, правительства скорее действительно предпочтут, чтобы разработчики встраивали «бэкдор» в свои системы, что позволяет им порой следить за тем, что делают люди.