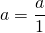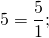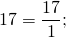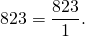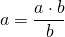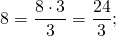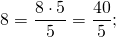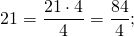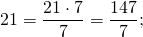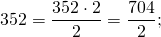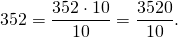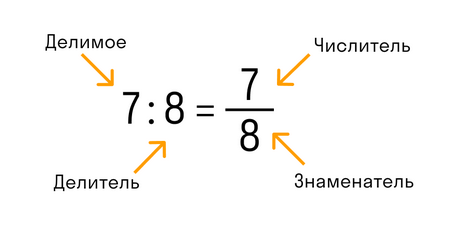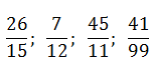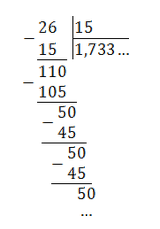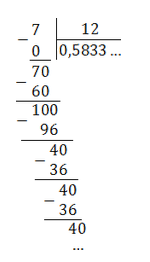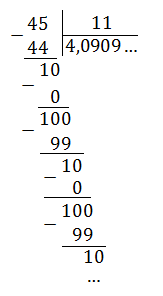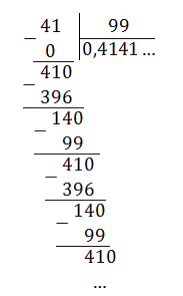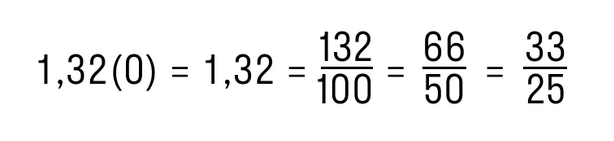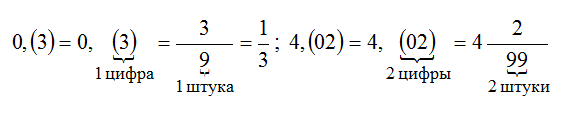Что значит представьте в виде дроби
Как целое число представить в виде дроби?
Неправильную дробь, у которой над и под дробной чертой одинаковые числа: 2/2, 11/11, 8/8 и другие, можно превратить в 1, потому что дробь — это частное, которое получается при делении числителя на знаменатель. Значит это и есть целое.
В математике целое принято принимать за единицу: отрезок, круг, яблоко, дом и т.д.
Рассмотрим несколько упражнений.
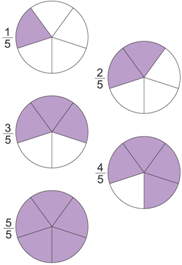
1. Назовите и запишите, какая часть круга закрашена?
Сколько всего пятых долей в целом круге?
2. На сколько частей разделили отрезок?
Сколько третьих долей во всем отрезке?
3. Строительные трубочки разделили на части.
Сколько частей в каждой трубочке? Сколько всего вторых долей в желтой трубочке? Сколько всего четвертых долей в красной трубочке? Сколько всего шестых долей в зеленой трубочке? Сколько всего восьмых долей в желтой трубочке? Сколько всего двенадцатых долей в последней красной трубочке?
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 77
Число в виде дроби
Любое целое число можно представить в виде дроби.
Чтобы записать целое число в виде дроби со знаменателем 1, нужно в числителе записать это число, а в знаменателе — единицу:
Целое число можно представить в виде дроби с любым знаменателем.
Чтобы записать целое число в виде дроби со знаменателем b, надо в числитель дроби записать произведение a∙b, а в знаменатель — b:
Записывая целое число в виде дроби, мы всегда получаем неправильную дробь.
2 Comments
иррациональное число нельзя представить в виде дроби
Да. Но понятие иррационального числа вводится в курсе алгебры.
Преобразование рациональных выражений: виды преобразований, примеры
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
Определение и примеры рациональных выражений
Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.
Следует начать с умножения, тогда получим, что
Производим представление полученного результата с исходное. Получим, что
Теперь выполняем вычитание:
После деления придем к рациональной дроби вида
Можно решить это иначе.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
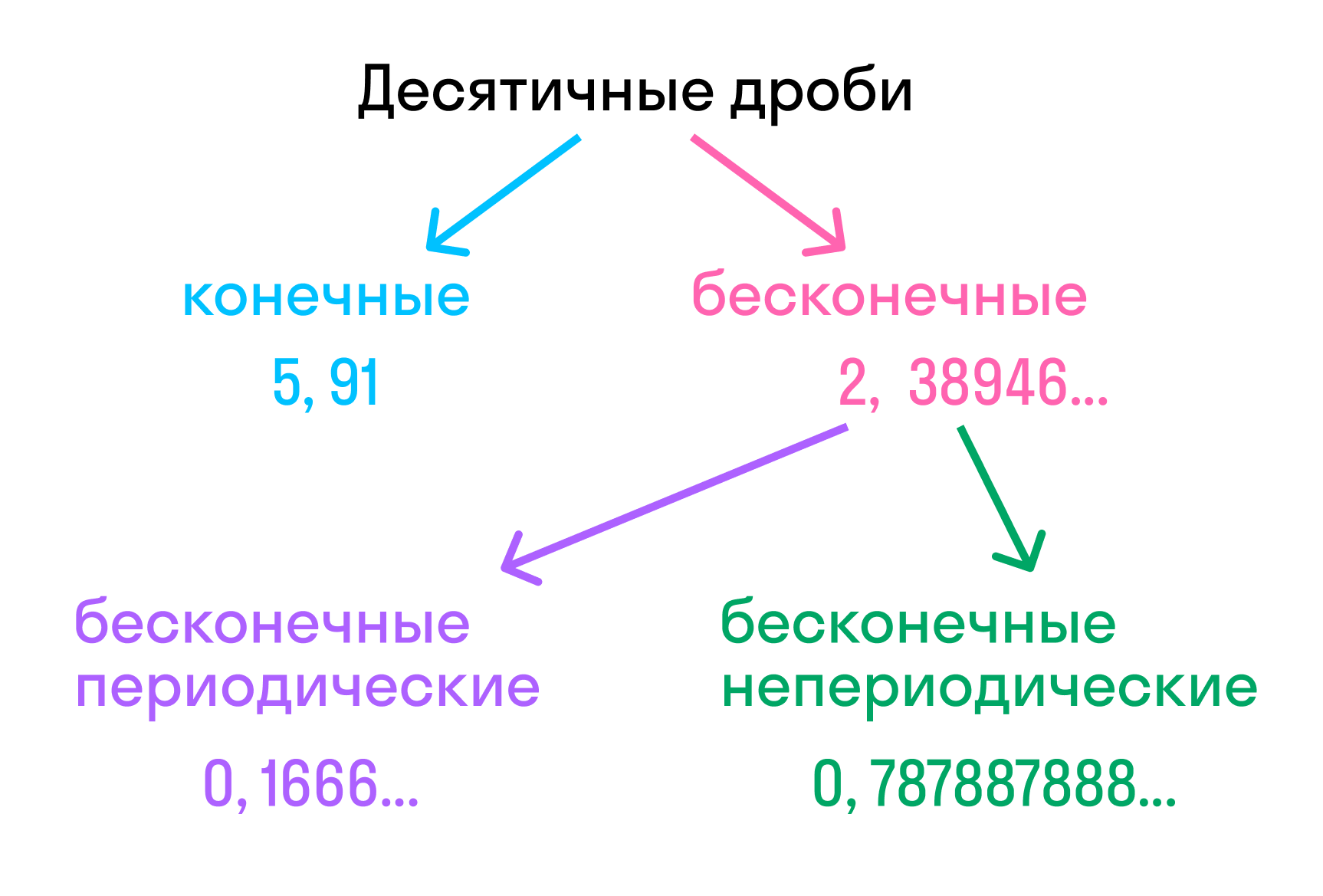
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
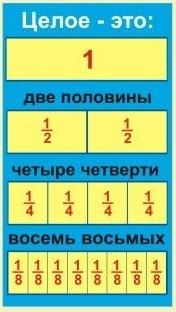
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Как перевести периодическую дробь
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:
Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.
Что будет происходить в процессе:
Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.
Пример. Перевести обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Определение периодической дроби
Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.
Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Виды периодических дробей: чистые и смешанные.
Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).
Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.
Рассмотрим примеры дробей, чтобы научиться определять части и период.
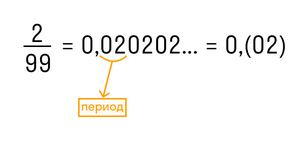
Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Читаем так: ноль целых три в периоде.
7/12 = 0,583333. = 0,58(3)
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.
17/11 = 1,545454. = 1,(54)
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Читаем так: одна целая пятьдесят четыре сотых в периоде.
25/39 = 0,641025 641025. = 0,(641025)
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.
Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.
пятьдесят четыре сотых в периоде.
9200/3 = 3066,666. = 3066,(6)
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.
Перевод периодической дроби в обыкновенную
Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
Рассмотрим пример, в котором период дроби отличен от нуля.
Как записать периодическую дробь 10,0219(37) в виде обыкновенной:
В нашем примере k = 2.
Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.
Теперь осталось подставить все найденные значения в формулу и получить ответ:
Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.
Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0
Перевод чистой периодической дроби в обыкновенную
Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:
Перевод смешанной периодической дроби в обыкновенную
Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.
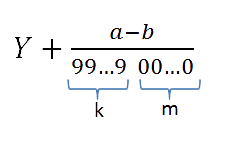
Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.
А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.
Например, запишем 2,34(2) в виде обыкновенной дроби: