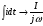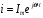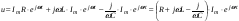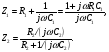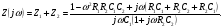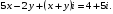Что значит практическая работа по математике

Что значит практическая работа по математике

Автор: Кабанова Светлана Дмитриевна

Организация: МОУ- СОШ д.Березина

Населенный пункт: Брянская область

Последнее время вопросу совершенствования преподавания математики уделяется большое внимание. Разрабатываются новые, более эффективные методы преподавания математики, совершенствуются формы организации уроков.

Важное условие совершенствования преподавания математики — усиление ее практической направленности.

Одним из путей решения этого вопроса является выработка у учащихся практических умений и навыков. Существенную роль в повышении эффективности обучения школьников играет сформированность у них практических умений и навыков геометрического характера (конструктивно-географических и измерительных), которые необходимы как для изучения математики, так и для повседневной деятельности.

Одной из форм обучения математики, способствующей развитию и воспитанию ценных графических и вычислительных навыков и умений, необходимых для конструирования и практической деятельности, на моих уроках являются лабораторные, лабораторно-графические и практические работы. Такие работы имеют большое воспитательное и образовательное значение. Они позволяют полнее и сознательнее уяснить математические зависимости между величинами; ознакомиться с измерительными и вычислительными инструментами и их применением на практике; установить более тесные связи между различными разделами курса математики и между различными школьными курсами.

Проведение лабораторных и практических работ с учащимися вносит разнообразие в мои уроки математики; повышает активность и самостоятельность учащихся на уроке; способствуют повышению качества знаний учащихся по математике; делает абстрактные теоретические положения понятными, доступными, наглядными.

При правильной организации работ воспитывается культура труда (умение организовать рабочее место, содержать его и инструменты в порядке), привычка к систематическому труду, уважение к работе, стремление к познанию и постоянному совершенствованию полученных знаний и навыков.

В методической литературе по математике нет строгой и четкой классификации лабораторных и практических работ.

Я выделяю 4 вида лабораторных работ.

1. Лабораторная работа, служащая для установления того или иного факта или положения.

5 класс. Тема «Треугольник».

Цель: Установить, что в любом треугольнике сумма всех углов треугольника равна 180ْ.

1. Начертите какой-нибудь треугольник. Обозначьте его.

2. Измерьте все его углы.

3. Найдите сумму их градусных мер.

2. Лабораторная работа, подводящая ученика к установлению определенной зависимости между величинами математического факта, требующего строгого доказательства.

7 класс. Тема «Соотношения между сторонами и углами треугольника».

Цель: Опытным путем установить зависимость между сторонами и углами треугольника.

1. Постройте треугольник с разными сторонами.

2. Измерьте стороны треугольника.

2. Измерьте все углы треугольника.

3. Сделайте вывод, как связаны между собой углы и стороны треугольника.

3. Лабораторная работа, которая содержит элементы исследовательского характера.

7 класс. Тема «Свойства высоты, биссектрисы, медианы в равнобедренном треугольнике».

Цель: установление свойств равнобедренного треугольника.

I. Постройте равнобедренный треугольник ABC (AB=BC).

1. Проведите высоту из вершины B к стороне AC.

2. Проведите медиану из вершины B к стороне AC.

3. Проведите биссектрису ÐB.

II. Постройте равнобедренный треугольник НМК (НМ=МК).

1. Проведите высоту из вершины М к стороне НК.

2. Проведите медиану из вершины М к стороне НК.

3. Проведите биссектрису ÐМ.

III. Сделайте вывод.

4. Если целью лабораторного занятия является выработка прочного навыка вычислений, конструирований и т. д., то такие занятия относятся к лабораторному практикуму по математике.

6 класс. Тема «Определение по карте расстояния между двумя пунктами земной поверхности».

Цель: Выработать навык работы с числовым масштабом.

1. Определите расстояние по железной дороге от станции А до станции В.

2. Определите длину реки.

К практическим работам отношу те самостоятельные работы учащихся, целью выполнения которых является проверка теоретически установленных фактов, соотношений, зависимостей в отдельном конкретном случае, применение теоретических знаний на практике, решение практических задач и т.д.

Выделяю следующие виды практических работ.

— с целью закрепления пройденного материала, выработки практических навыков;

— с целью повторения пройденной темы;

— с целью повторения, обобщения нескольких тем;

— с целью подготовки к изучению нового материала.

7 класс. Тема «Определение функции».

Цель: закрепить первоначальное представление о функции, посредством исследования зависимости площади прямоугольника данного периметра от длин его сторон.

I. Периметр прямоугольника 24 см, а его основание х см.

1.Найдите длину второй стороны.

2.Задайте формулой зависимость площади S (см 2 ) прямоугольника от длин его сторон.

Источник

Практические работы на уроках математики

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Практические работы в процессе обучения математики в начальных классах. Автор проекта: учитель начальных классов МОУ «Бендерская средняя общеобразовательная школа № 15» Цуркан Людмила Анатольевна

АКТУАЛЬНОСТЬ Существенную роль в повышении эффективности обучения младших школьников играет сформированность у них практических умений и навыков, которые необходимы как для изучения математики, так и для повседневной деятельности. Практические работы позволяют полнее и сознательнее уяснить математические зависимости между величинами; ознакомиться с измерительными и вычислительными инструментами и их применением на практике; установить более тесные связи между различными разделами курса математики и между различными школьными курсами.

При изучении элементов геометрии в начальных классах, для формирования практических навыков предлагается так же использовать «различные практические упражнения». К этим упражнениям относится «закрашивание, выделение признаков,конструирование,исследование.

К практическим можно отнести задание «оживить» геометрическую фигуру, «живые построения» используются когда, например, «четверым учащимся предлагают взяться за руки и образовать квадрат, изобразить куб, цилиндр, пирамиду». Прием «живого построения» предлагается использовать при усвоении компонентов сложения и вычитания, при знакомстве с задачами на движение, при показе математических действий.

На уроках-практикумах по математике дети: Сравнивают, уравнивают по длине, массе, объему, количеству, высоте, цене, площади. Измеряют длину, скорость, рост, вес. Вычисляют площадь, периметр реальных объектов. Работают с измерительными приборами, применяемыми в реальной жизни: с весами, часами, секундомерами, термометрами, линейками, сантиметровыми лентами, всевозможными емкостями. Решают текстовые задачи с помощью пласти лина, камней, кубиков. Между тем математика всегда была и всегда будет основным учебным предметом общего образования. Надо обучать детей, чтобы математическое образование «пригодилось для жизни, для дела, любви, радости».

3. Тема урока: «Ломаная линия» Оборудование: проволока, спички, счетные палочки, пластилин, полоски бумаги, клей. Соберите на партах ломаную. Продемонстрируйте свои модели. Из чего вы сделали ломаные линии? (Из отдельных палочек, частей, кусочков…) Из каких элементов состоит ваша ломаная? ( Из отрезков-звеньев) Сколько отрезков в вашей ломаной? А сколько может быть? Значит, из чего состоит ломаная линия? (Ломаная линия состоит из отрезков-звеньев.) Вывод: Ломаная линия – это несколько отрезков, при которой конец первого является началом второго, а конец второго – началом третьего и т.д.

Изучение состава числа

Таким образом, можно сделать вывод, что правильная организация практической и самостоятельной работы учащихся начальных классов является важным элементом развития школьников.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-278574

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В МГПУ сформулировали новые принципы повышения квалификации

Время чтения: 4 минуты

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Выполнение практических работ на уроках математики

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Выполнение практических работ на уроках математики.

… Ни один наставник не должен забывать,

что его главнейшая обязанность состоит

в приучении воспитанников к умственному труду

и что эта обязанность более важна,

нежели передача самого предмета.

Важным началом, обуславливающим содержание, организацию и методы преподавания математики в школе, должна стать тесная связь обучения с жизнью, трудом, практикой. Осуществление этого принципа будет содействовать выработке у учащихся правильного представления о математике как науке о пространственных формах и количественных отношениях реального мира, раскрытию перед ними значения математики в технике и повседневной жизни.

В процессе преподавания математики необходимо проводить систематическую и целенаправленную работу по развитию логического мышления учащихся. Для этого очень важное место занимают на уроках математики практические задания.

Практические задачи заставят ученика действовать: рисовать, чертить, вырезать, играть, измерять отрезки, находить вес, площадь объем, добывать необходимые для решения задач сведения, составлять планы, сметы, диаграммы, денежные расчеты и. т. п.

С помощью решения таких задач учащиеся развивают инициативу, самостоятельность, конструктивные способности, находчивость и смекалку, т. е. все те качества, какие им нужны будут в дальнейшей их практической деятельности.

Практические задачи в начальных классах с первых же шагов школьной жизни учащиеся вырабатывают в них умение владеть карандашом, линейкой, циркулем, ножницами и постепенно вводят в круг таких вопросов, которые связаны или со школьной жизнью или с жизнью общества.

Практические упражнения и задачи могут быть использованы как классной работе под руководством учителя, так и в качестве заданий для самостоятельной работы учащихся. Многие задачи и упражнения можно использовать как проверочные, тренировочные или контрольные работы.

Например: 1)Для работы в классе под руководством учителя.

Через две точки А и Б, поставленные на доске, вызванные учащиеся могут провести ряд различных линий.

Учет работы по глазомерному измерению.

Рулеткой или верёвкой

Расстояние от края доски до стены

Учитель предлагает учащимся оценить на глаз начерченный на доске, или отбитый шнуром на полу, или указанный учителем на каком – либо предмете (длина рамки, высота двери и. т. п.) отрезок т и записать в графу «на глаз», а затем двое учащихся (каждый раз разные) измеряют этот отрезок линейкой или рулеткой. Результат измерения записывают на доске, а дети вписывают его в следующую графу и вычисляют ошибку.

в) Начертите три разных треугольника, определите на глаз, сумму длин всех сторон (периметр) каждой фигуры и затем проверьте по линейке. Результаты измерений запишите.

Уроки по математике в начальных классах должны быть оборудованы наглядными пособиями и измерительными инструментами, линейками, треугольниками, рулетками, различными фигурами, одинаковыми картинками или игрушками, палочками, пуговицами, камешками, орехами, желудями, шнурами, веревками разных длин и. т. п.). Все это должно храниться в классном шкафу.

Сделайте такую же таблицу и вычислите произведение чисел а×в при условии, что множитель (в) будет постоянно равно 2, а множимое будет принимать значения от 1 до 10 по порядку.

Как отсюда можете сделать вывод.

б) Начертите один под другим 3 кружочка, а через строчку направо еще 3 кружочка и так 10 раз. У вас получится такая фигура из кружочков.

О О О О О О О О О О

О О О О О О О О О О

О О О О О О О О О О

Подсчитайте четырьмя способами ( сложением и умножением ) количество всех кружочков.

(3+3… +3=30 ; 3×10=30; 10×3=30; 10+10+10=30)

После того как дети своими словами объяснят определения окружности, радиуса и диаметра, желательно вывесить на стену плакат с определениями этих элементов.

Можно ли сказать, что при делении круга на две равные части и окружность разделилась на две равные части; что при делении круга на 4 равные части и окружность разделилась на 4 равные части и. т. д.

С минутой можно ознакомить различными способами. Можно предложить промолчать всем одну минуту. В течение минуты посчитать вслух, начиная с единицы. Вслед за таким счетом вслух можно предложить детям в таком же темпе посчитать молча, про себя. Можно предложить посчитать шепотом в более быстром темпе, кто до какого числа сумеет досчитать в минуту. Можно посчитать вслух что-нибудь из книги для чтения и. т. п.

Для освоения меры времени «час» можно предложить детям дома заметить по часам, сколько страниц печатного текста каждый из них прочтет за 20 минут, и вычислить сколько страниц он с может прочитать за один час. А в классе, сколько каждый из учеников решит, скажем за 15 минут каких-либо упражнений по арифметике, а затем вычислить, сколько таких же упражнений он сделал бы за 1 час.

При ознакомлении с сутками надо непременно объяснить, что середину ночи называют полночью, середину дня – полднем и что счет суток начинают с полночи. За время суток часовая стрелка обязательно делает два полных оборота и поэтому счет часов ведется от полуночи до полудня и от полудня до полуночи и поэтому каждая цифра на циферблате обозначает и дневные и ночные часы. Пояснить также, что слово «сутки» заменяют словом «день» и говорят например, что в неделе 7 дней (вместо 7 суток).

Необходимо научить детей определять время по часам. Этому надо учить с помощью циферблатов, которые должны быть у каждого ученика, и при помощи настоящих часов, например, будильников.

Неплохо провести ряд работ, связанных с отрывным календарём или с табелем-календарём. Например, дома ученики могут проследить по отрывному календарю, как изменяется долгота дня в данном месяце и подсчитать на сколько минут убавится или прибавится в этом месяце день. По табелю-календарю проследить, сколько в данном месяце воскресений, понедельников, сколько учебных дней в 1 четверти, во 2-ой четверти учебного года и. т. д. Все задачи связанные с календарём выполняются учащимися с удовольствием, они имеют большое жизненно практическое значение.

При изучении мер площади необходимо, чтобы модели единиц квадратных мер ученики сделали сами из бумаги, картона или фанеры.

Начать изучение квадратных мер лучше с квадратного дециметра, чертёж которого хорошо помещается в тетради. В левом нижнем углу квадратного дециметра надо сделать чертёж квадратного сантиметра, в нём чертёж квадратного миллиметра (чертежи делаются карандашом). Все эти чертежи надо затушевать штрихами различной плотности. Затем модели квадратного дециметра и сантиметра изготавливаются детьми из плотной бумаги,

Квадратный метр должен быть разделён на квадратные дециметры, а в одном из углов сделан квадратный сантиметр и в нём квадратный миллиметр (для сравнения мер)

Для лучшего освоения мер, полезно решать практические задачи, в которых ученики будут непосредственно иметь дело с этими мерами.

2) Постройте в тетради квадрат со стороной 12 см. 5 мм.. Определите его площадь путём подсчёта клеток и вычислением.

3) Ученик сделал чертёж прямоугольника, в котором длина втрое больше ширины, а сумма длины и ширины составляла вместе 12 см. Постройте этот прямоугольник и определите его площадь.

Эту задачу предлагают решить двумя способами: способом частей и способом составления уравнения:

а) Сколько частей составляют 12 см.?

б) Сколько сантиметров приходится на 1 часть?

Источник

Практические работы по математике

Методические указания по выполнению практических работ по математике, 2 курс, 1 семестр

Просмотр содержимого документа
«Практические работы по математике»

Федеральное государственное бюджетное образовательное учреждение

«Ростовский государственный университет путей сообщения»

Волгоградский техникум железнодорожного транспорта

(ВТЖТ – филиал РГУПС)

23.02.06 Техническая эксплуатация подвижного состава

Преподаватель Марченко Л.Е.

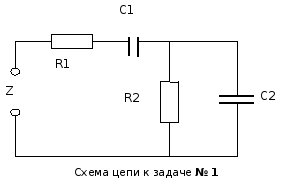
Практическая работа № 1

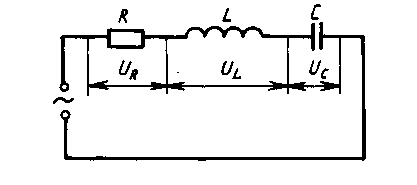
«Нахождение полного сопротивления электрической цепи

переменного тока с помощью комплексных чисел».

1) Систематизировать и обобщить знания студентов в области комплексных чисел;

2) Выработать навыки и умения применять теорию комплексных чисел в решении физических задач;

3) Развивать умения пользоваться опорным конспектом и дидактическим материалом для постановки задачи и её выполнения в ходе решения;

4) Воспитывать ответственное отношение к учебному труду, настойчивости для достижения конечных результатов.

Расчет линейных электрических схем переменного тока аналогичен расчету электрических схем постоянного тока. В обоих случаях составляют систему алгебраических уравнений по методам, основанным на законах Ома и Кирхгофа.

Для схем постоянного тока уравнения составляют по действительным значе­ниям напряжений, токов, сопротивлений и проводимостей. В схемах же переменного тока для уравнений приме­няют комплексные (символические) величины: U, I, Z=R+ jX. При этом все параметры записывают в виде комплексных чисел в алгебраической показательной или тригонометрической форме. При переходе от интегрально-дифференциальных уравнений дифференцирование мгновенного значения заменяют умножением jω на соответствующую комплексную величину, а интегри­рование — делением комплексной величины на jω:

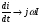
Алгоритм расчета комплексным методом

2. Комплексные сопротивления Z = R + jX всех ветвей схемы записывают в зависимости от выбранного метода расчета.

4. При необходимости переходят к мгновенному значению i = I_m cos (ωt + φ).

В любой момент времени сумма мгновенных значений на­пряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения (Рис. 1):

Во всех последовательно включенных элементах цепи из­менения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со ско­ростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:

Колебания напряжения на резисторе совпадают по фазе с ко­лебаниями силы тока

,

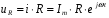
а колебания напряжения на катушке опережают по фазе колебания силы тока на /2.

,

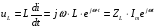
где ,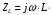

колебания напряжения на конденсаторе отстают по фазе на /2 от колебаний силы тока

,

, (емкостное сопротивление)

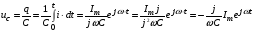
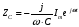
Поэтому уравнение можно записать так:

согласно закона Ома: 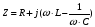– комплексное сопротивление.

Таким образом, мы видим, что действительное число это активное сопротивление, а мнимое число – реактивное. Общее комплексное сопротивление можно найти сложением комплексных чисел, что значительно проще метода векторных диаграмм особенно для разветвленных цепей. Покажем это на примере задачи № 1.

Получить формулу, описывающую комплексное сопротивление Z двухполюсника с двумя резисторами и двумя конденсаторами.

Искомая величина Z является суммой сопротивлений Z₁ и Z₂ двух более простых цепей, одна из которых образована последовательным, а другая параллельным включением элементов:

Приводя к общему знаменателя, получаем

Следующую задачу решить самостоятельно.

Задания для самостоятельного решения

Найдите действительные числа и из условия равенства двух комплексных чисел: 1) ; 2) ; 3)

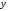
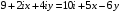
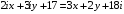
Выполните деление в тригонометрической форме:

Практическая работа № 2

«Построение графа по условию ситуационных задач».

1) Систематизировать и обобщить знания студентов по теории графов;

2) Выработать навыки и умения применять теорию графов в решении ситуационных задач;

3) Развивать умения пользоваться опорным конспектом и дидактическим материалом для построения графа в ходе решения задачи;

4) Воспитывать ответственное отношение к учебному труду, аккуратность в оформлении решения задачи.

Задача №1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Задача № 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.

Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу?

Решение: Занумеруем последовательно клетки доски:

А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:

Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – представление решения с помощью графа. Заметим, что не каждая картинка такого вида будет называться графом. Например, если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет.

Задача №3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, то есть степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза).

Ответ. Соединить телефоны таким образом невозможно.

Теорема: Любой граф содержит четное число нечетных вершин.

Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.

Есть еще одно важное понятие, относящееся к графам – понятие связности.

Граф называется связным, если любые две его вершины можно соединить путем, то есть непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.

Задача №4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.

Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:

Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.

Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: «Доказать, что граф дорог страны Семерка связен».

Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких «кусков», каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:

Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов.

Рассмотрим пример задачи, в которой используется компонента связности:

Задача №5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.

Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.

Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру, не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, то есть существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Задача №6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?

Решение: Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.

Сейчас мы доказали теорему об Эйлеровых графах:

Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.

Задания для самостоятельного решения

2.1. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9?

2.2. В государстве 100 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве?

2.3. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?

2.4. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей?

2.5. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?

2.6. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.

Практическая работа № 3

«Применение обыкновенных дифференциальных уравнений при решении прикладных задач».

1) Систематизировать и обобщить знания студентов по решению дифференциальных уравнений;

2) Выработать навыки и умения применять теоретические знания в области дифференциальных уравнений при решении прикладных задач;

3) Развивать умения пользоваться теоретическим материалом для постановки задачи и её выполнения в ходе решения;

4) Воспитывать ответственное отношение к учебному труду, настойчивости для достижения конечных результатов.

Решение: Согласно условию, имеем

Решение: Пусть угловая скорость вращения диска в момент времени тогда замедления вращения диска под воздействием силы трения равно

Согласно условию, где коэффициент пропорциональности. Разделив переменные и интегрируя, получим

Подставив значение в равенство (2), получим

Найдем скорость вращения диска в момент времени с. Подставим в равенство (3) значение :

Задания для самостоятельного решения

3.5. Радий распадается со скоростью, пропорциональной начальному его количеству. Через сколько лет распадется половина начального его количества? Принять (единица измерения времени – год).

Практическая работа № 4

«Решение задач с применением числовых рядов».

1) Систематизировать и обобщить знания студентами числовых рядов;

2) Выработать навыки и умения применять теорию рядов в ходе решения практических задач различной сложности;

3) Развивать умения пользоваться дидактическим материалом для постановки задачи и её выполнения в ходе решения, грамотно оформлять решение задачи;

4) Формирование умения рационально, аккуратно оформлять задание на доске и в тетради.

Задача № 1: Найдите первые пять членов ряда по его заданному общему члену.

Решение: Находим частичные суммы членов ряда:

Задача № 3: Найти сумму членов ряда

По определению суммы ряда:

Задача № 4: Исследовать ряд на сходимость, применяя признак Даламбера:

Решение: Преобразуем выражение :

Ряд сходится по признаку Даламбера.

Решение: При данный ряд превращается в числовой ряд

Исследуем сходимость этого ряда по признаку Даламбера. Имеем

то есть ряд сходится.

который расходится, так как не выполняется необходимый признак сходимости ряда.

Это знакочередующийся ряд, который согласно признаку Лейбница, сходится.

Задача № 6: Найти промежуток сходимости степенного ряда:

Задания для самостоятельного решения

4.1. Найдите первые пять членов ряда по его заданному общему члену:

4.2. Найдите п-й член ряда по его данным первым членам:

4.3. Исследовать ряд на сходимость:

4.4. Определить радиус сходимости ряда:

4.5. Найти промежуток сходимости степенного ряда:

Практическая работа № 5

«Решение прикладных задач с использованием комбинаторики».

1) Обобщить понятие комбинаторной задачи, видов соединений;

2) Отработать умение решать задачи на применение формул перестановок, размещений, сочетаний;

3) Развивать умение обобщать, систематизировать на основе сравнения, делать вывод;

4) Воспитание коммуникативной и информационной культуры студентов.

Задача № 1: Сколькими способами могут быть расставлены 8 участниц финального забега на 8 беговых дорожках?

Решение: Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что

Задача № 2: Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?

Решение: Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо предметами, либо порядком следования предметов. Значит, в этом примере идет о размещениях из 8 элементов по 4.

Задача № 3: Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

Решение: Каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3.

Задача № 4: Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?

Решение: Выбрать 3 яблока из 9 можно способами, а выбрать 2 груши из 6 можно способами. Так как при каждом выборе яблок груши можно выбрать способами, то сделать выбор фруктов, о котором говорится в задаче, можно способами.

Задания для самостоятельного решения

5.1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?

5.2. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?

5.3. Сколькими способами из 10 человек можно выбрать комиссию, состоящую из 5 человек?

5.5. Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд. Найдите число возможных комбинаций, если: а) Олег должен находиться в конце ряда; б) Олег должен находиться в начале ряда, а Игорь – в конце ряда; в) Олег и Игорь должны находиться рядом.

5.8. Сколько существует перестановок букв слова «пирамида», в которых буквы п, и, р стоят рядом?

5.9. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?

5.10. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихов, так, чтобы сборники стихов стояли рядом в произвольном порядке?

5.11. Имеется девять различных книг, четыре из которых – учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?

5.12. В соревнованиях по футболу участвовало 12 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника. Сколько всего игр было сыграно?

Практическая работа № 6

«Решение прикладных задач на нахождение вероятности события».

1) Систематизировать знания основных определений, формул теории вероятностей;

2) Выработать умения и навыки применять теоретический материал при решении вероятностных задач различного уровня;

3) Активизировать самостоятельную деятельность студентов;

4) Формирование умения аккуратно оформлять задание в тетради.

Задача № 1. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.

Задача №2: Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).

Задача № 3. В билете 3 раздела. Из 40 вопросов первого раздела студент знает 30 вопросов, из 30 вопросов второго – 15, из 30 вопросов третьего – 10. Определить вероятность правильного ответа студента по билету.

Задача № 4. На склад ежедневно поступают детали с трех предприятий. С первого – 30 деталей, со второго – 20и с третьего – 40. Установлено, что 2, 4 и % продукции этих предприятий, соответственно, имеют дефекты. Найти вероятность того, что взятая наудачу деталь будет дефектна.

Решение: Обозначим: взятая наугад деталь дефектна; деталь изготовлена на первом предприятии; деталь изготовлена на втором предприятии; деталь изготовлена на третьем предприятии. События и образуют полную группу несовместных событий и

Условные вероятности события равны:

Задача №5: Случайная величина задана законом распределения:

Источник