Что значит открытое множество
Открытое множество
Откры́тое мно́жество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии.
Термин «открытое множество» применяется к подмножествам топологических пространств и никак не характеризует «само» множество (ни в смысле теории множеств, ни даже в смысле индуцированной на нём топологической структуры). [1] [2]
Содержание
Евклидово пространство
Пусть 
есть некоторое подмножество евклидова пространства. Тогда 
называется открытым, если 
0,» border=»0″ /> такое что 
, где 
— ε-окрестность точки 
Иными словами, множество открыто, если любая его точка является внутренней.
Например, промежуток как подмножество действительной прямой является открытым множеством.
Метрическое пространство
Пусть 
— некоторое метрическое пространство, и 
. Тогда называется открытым, если 0,» border=»0″ /> такое что , где 
— ε-окрестность точки 
относительно метрики 
.
Топологическое пространство
Обобщением приведённых выше определений является понятие открытого множества из общей топологии.
Топологическое пространство 
по определению содержит «перечень» своих открытых подмножеств 
— «топологию», определённую на 
. Подмножество , такое, что оно является элементом топологии (то есть 
), называется открытым множеством относительно топологии .
См. также
Сноски
Полезное
Смотреть что такое «Открытое множество» в других словарях:
Открытое множество — точечное множество, не содержащее предельных точек (См. Предельная точка) дополнительного к нему множества (см. Множеств теория). Любая точка О. м. является внутренней, т. е. имеет Окрестность, содержащуюся целиком в О. м. Наряду с… … Большая советская энциклопедия
Открытое множество (топология) — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия
Множество Жюлиа — Множество Жюлиа. Точнее, это не само множество (которое в данном случае состоит из несвязных точек и не может быть нарисовано), а точки из его окрестности. Чем ярче точка, тем ближе она к множеству Жюлиа и тем больше итераций ей нужно, чтобы уйти … Википедия
Множество Джулия — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Множество Фату — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Открытое подмножество — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия
Замкнутые и открытые множества
Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.
Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек
Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.
1. Пересечение любого числа замкнутых множеств замкнуто.
2. Сумма любого числа открытых множеств есть открытое множество.
3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.
4. Если множество замкнуто, то его дополнение открыто и обратно.
Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.
В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).
Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.
Канторово совершенное множество
Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.
Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.
Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.
Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.
Открытое множество
Смотреть что такое «Открытое множество» в других словарях:
Открытое множество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. Термин «открытое множество» применяется к подмножествам топологических пространств и никак … Википедия
Открытое множество (топология) — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия
Множество Жюлиа — Множество Жюлиа. Точнее, это не само множество (которое в данном случае состоит из несвязных точек и не может быть нарисовано), а точки из его окрестности. Чем ярче точка, тем ближе она к множеству Жюлиа и тем больше итераций ей нужно, чтобы уйти … Википедия
Множество Джулия — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Множество Фату — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Открытое подмножество — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия
Открытое множество (топология)
Откры́тое мно́жество в математическом анализе, геометрии — это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии.
Термин «открытое множество» применяется к подмножествам топологических пространств и никак не характеризует «само» множество (ни в смысле теории множеств, ни даже в смысле индуцированной на нём топологической структуры). [1] [2]
Содержание
Евклидово пространство
Пусть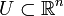 
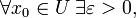
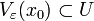
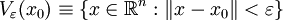
есть некоторое подмножество евклидова пространства. Тогда U называется открытым, если 
такое что 
, где 
— ε-окрестность точки x0. Иными словами, множество открыто, если любая его точка является внутренней.
Например, промежуток как подмножество действительной прямой является открытым множеством.
Метрическое пространство
Топологическое пространство
Обобщением приведённых выше определений является понятие открытого множества из общей топологии.
См. также
Сноски
Полезное
Смотреть что такое «Открытое множество (топология)» в других словарях:
Открытое множество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. Термин «открытое множество» применяется к подмножествам топологических пространств и никак … Википедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия
ТОПОЛОГИЯ — раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация это деформация фигуры, при которой не… … Энциклопедия Кольера
Открытое покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Дискетная топология — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ОТКРЫТОЕ МНОЖЕСТВО
Смотреть что такое «ОТКРЫТОЕ МНОЖЕСТВО» в других словарях:
Открытое множество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. Термин «открытое множество» применяется к подмножествам топологических пространств и никак … Википедия
Открытое множество — точечное множество, не содержащее предельных точек (См. Предельная точка) дополнительного к нему множества (см. Множеств теория). Любая точка О. м. является внутренней, т. е. имеет Окрестность, содержащуюся целиком в О. м. Наряду с… … Большая советская энциклопедия
Открытое множество (топология) — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия
Множество Жюлиа — Множество Жюлиа. Точнее, это не само множество (которое в данном случае состоит из несвязных точек и не может быть нарисовано), а точки из его окрестности. Чем ярче точка, тем ближе она к множеству Жюлиа и тем больше итераций ей нужно, чтобы уйти … Википедия
Множество Джулия — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Множество Фату — Множество Жюлиа Множество Жюлиа В голоморфной динамике, множество Жюлиа рационального отображения … Википедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Открытое подмножество — Открытое множество в математическом анализе, геометрии это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии. Термин «открытое множество»… … Википедия