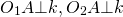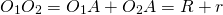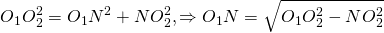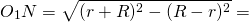Что значит окружности касаются внешним образом

Касание двух окружностей

Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.

Общая точка двух окружностей называется точкой касания окружностей.

Касание окружностей может быть внешним и внутренним.

Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.

Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.

Касающиеся окружности имеют только одну общую точку — точку касания.

Центры касающихся окружностей и их общая точка касания лежат на одной прямой.

При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.

Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

При внутреннем касании расстояние между центрами окружностей равно разности радиусов:

Источник

Касательные к окружности

В обычной жизни ты очень хорошо представляешь себе, что значит слово «коснуться».

И вот представь себе, в математике тоже существует такое понятие.

В этой теме мы разберёмся с выражениями «прямая касается окружности» и «две окружности касаются».

Касательные к окружности. Коротко о главном

Касательная – прямая, которая имеет с окружностью только одну общую точку.

Касательная окружности перпендикулярна радиусу, проведённому в точку касания.

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла: \( \displaystyle \angle CAB=\frac<1><2>\angle AOB\), где:

Касание окружностей: если две окружности касаются, то точка касания лежит на прямой, соединяющей их центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей:

Внешнее касание

Внутреннее касание

Для двух окружностей с центрами \( \displaystyle <>\) и \( \displaystyle <_<1>>\), и радиусами \( \displaystyle R=OA\) и \( \displaystyle r=<_<1>>A\):

Касательные к окружности. Определения и основная теорема

Прямая касается окружности, если имеет с ней ровно одну общую точку.

Такая прямая называется касательной к данной окружности.

Посмотри-ка внимательно: очень похоже на жизнь, не правда ли? Прямая на картинке лишь чуть-чуть дотрагивается до окружности, касается ее.

Ну вот, и точно так же:

Две окружности касаются, если имеют ровно одну общую точку.

Что же тебе нужно знать о касательных и касающихся окружности?

Самая важная теорема гласит, что:

Радиус, проведённый в точку касания, перпендикулярен касательной.

Запомни это прямо как таблицу умножения! Все остальные факты о касательных и касающихся окружностях основаны именно на этой теореме.

Доказывать её мы здесь не будем, а вот как эта самая важная теорема работает, увидим сейчас несколько раз.

Угол между касательной и хордой

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.

Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».

Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу.

То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!

Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.

Смотри, хорда \( \displaystyle AB\) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла \( \displaystyle BAC\), а другая дуга – внутри угла \( \displaystyle BAD\).

И теорема об угле между касательной и хордой говорит, что \( \displaystyle \angle CAB\) равен ПОЛОВИНЕ угла \( \displaystyle AOB\), \( \displaystyle \angle DAB\) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла \( \displaystyle AOB\).

При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?

Сейчас и увидим. \( \displaystyle OA\) – радиус, \( \displaystyle AC\) – касательная.

Значит, \( \displaystyle \angle OAC=90<>^\circ \).

И осталось вспомнить, что сумма углов треугольника \( \displaystyle AOB\) равна \( \displaystyle 180<>^\circ \).

Здорово, правда? И самым главным оказалось то, что \( \displaystyle \angle OAC=90<>^\circ \).

Равенство отрезков касательных

Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:

А ещё более удивительный факт состоит в том, что:

Отрезки касательных, проведённых из одной точки к одной окружности, равны.

То есть, на нашем рисунке, \( \displaystyle AB=AC\).

И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.

Проведём радиусы \( \displaystyle OB\) и \( \displaystyle OC\) и соединим \( \displaystyle O\) и \( \displaystyle A\).

\( \displaystyle OB\) – радиус.

\( \displaystyle AB\) – касательная, значит, \( \displaystyle OB\bot AB\).
Ну, и так же \( \displaystyle OC\bot AC\).

Получилось два прямоугольных треугольника \( \displaystyle AOB\) и \( \displaystyle AOC\), у которых:

(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).

Но раз \( \displaystyle \Delta AOB=\Delta AOC,\) то\( \displaystyle AB=AC\). УРА!

И ещё раз повторим – этот факт тоже очень важный:

Отрезки касательных, проведённых из одной точки, – равны.

И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.

Для любой прямой \( \displaystyle AD\), пересекающей окружность,\( \displaystyle AD\cdot AC=A<^<2>>\), где \( \displaystyle AB\) – отрезок касательной.

Хитроумными словами об этом говорят так:

«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».

Страшно? Не бойся, помни только, что в буквах это:

Общая касательная к двум окружностям

Прямая, которая касается двух окружностей, называется их общей касательной.

Общие касательные бывают внешние и внутренние. Смотри на картинки.

Две внутренние общие касательные:

Две внешние общие касательные:

А всего – четыре! Не больше, но может быть меньше.

Есть только две внешние общие касательные.

Или так: одна внутренняя и две внешних.

А может быть вообще так:

Только одна общая касательная.

И снова факты:

Длины отрезков двух внутренних общих касательных равны

Длины отрезков двух внешних общих касательных равны.

НО! При этом: внешние и внутренние касательные – разные! (а некоторых, может, и вообще нет…)

Касающиеся окружности

Касание окружностей бывает внешним и внутренним.

Вот такая картинка называется «окружности касаются внешним образом»:

А вот такая картинка называется «окружности касаются внутренним образом»:

Что же самое главное нужно знать?

Если две окружности касаются, то точка касания лежит на прямой, соединяющей центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей.

Если тебе показалось слишком длинно – посмотри картинку. Может быть ещё так:

Ура, теперь ты полностью вооружён на борьбу с касательными – дерзай! 🙂

Источник

Окружности касаются внешним образом

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

Обозначим O₁A=r, O₂C=R.

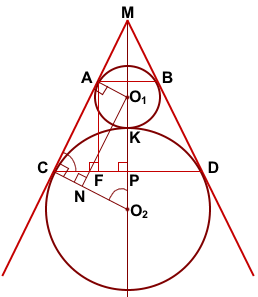
Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Рассмотрим прямоугольный треугольник O₁O₂N.

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).

Источник