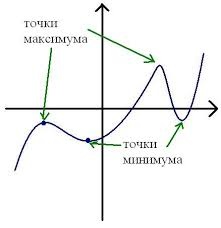
Что значит найти точку минимума функции
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Как найти точку максимума функции?
Глобальный и локальный максимум
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.
Область допустимых аргументов
Асимптоты
Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.
Производная и экстремумы
Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.
1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.
Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
Задание 11 Профильного ЕГЭ по математике
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
Найдем знаки производной.


7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если 


8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции

10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. 
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Как найти точки минимума и максимума функции
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
Точка минимума, минимум функции
Минимум функции — значение функции в точке минимума \(x_0\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Максимум функции — значение функции в точке максимума \(x_0\)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке \(x=x_0,\) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
Найти область определения функции — D(y).
Определить производную — f ‘(x).
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию \(f(x)=x^3-3x^2.\)
Решение задачи по алгоритму:
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
5) Найдем значение экстремумов функции.
Задача 2
Задача 3
Докажите, что функция \(f(x)=x^5+2x^3-4\) возрастает на всех числовой прямой.
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого