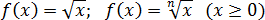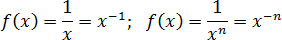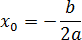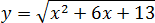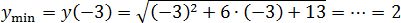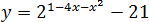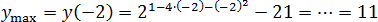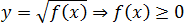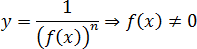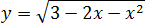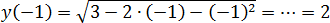Что значит найти наименьшее значение квадратичной функции
Наибольшее и наименьшее значение функции.
Графические примеры наибольших и наименьших значений функций на отрезках и интервалах.
Эта парабола на области определения имеет только наименьшее значение. Наибольшего значения нет, так как её ветви уходят в бесконечность.
На отрезке [a;b] есть и наибольшее, и наименьшее значения. В этом примере наименьшее значение достигается во внутренней точке отрезка и совпадает с экстремумом (минимумом) функции, наибольшее — на одном из концов отрезка. В данном случае это y = f(b).
Функция рассматривается на интервале (a;b). В этом случае краевые точки a и b не входят в область определения функции на оси Ox, и, соответственно, не определены значения функции f(a) и f(b) на оси Oy. Однако, можно вычислить сколь угодно близкие к ним значения. Поэтому в этом примере функция имеет наименьшее значение, но не достигает наибольшего, его нет.
На этом полуинтервале (a;b] есть наибольшее значение приведенной функции, но наименьшего нет.
Кубическая парабола на области определения имеет два экстремума, но наименьшего и наибольшего значений не достигает: её ветви уходят в бесконечность. E(f) = (−∞; +∞) — область значений кубической параболы.
Здесь на отрезке [a;b] наибольшее значение достигается в точке максимума, а наименьшее в краевой точке отрезка.
Если вместо отрезка [a;b] рассматриваем интервал (a;b) с теми же концами, то наименьшего значения нет.
Непрерывная функция, заданная на отрезке, всегда имеет наибольшее и наименьшее значения. Но, если функция имеет разрывы, то могут быть различные варианты, как для интервалов, так и для отрезков. Посмотрите на этот график разрывной функции, заданной на отрезке [−2;3]. Здесь функция не имеет наибольшего значения: перед точкой разрыва она возрастает и достигает значений больших, чем в других частях отрезка, но наибольшего не достигает, так как в предполагаемой точке максимума x = 2 она определена другим значением, не у = 2, а y = −1.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Как решать задачи B15 без производных
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность.
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Другими словами, для возрастающей функции Для убывающей функции все наоборот:
Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:
f ( x ) = log a x ( a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:
Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Задача. Найдите наименьшее значение функции:
Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент
x 0 = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.
Корень монотонно возрастает, значит точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,
x 0 = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:
Задача. Найдите наибольшее значение функции:
В показателе стоит квадратичная функция Перепишем ее в нормальном виде:
Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Аргумент логарифма должен быть положительным:
y = log a f ( x ) ⇒ f ( x ) > 0
Арифметический квадратный корень существует только из неотрицательных чисел:
Знаменатель дроби не должен равняться нулю:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.
Выписываем область допустимых значений (ОДЗ):
3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒
Теперь найдем вершину параболы:
Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x 0 = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) =
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Основные определения
Начнем, как всегда, с формулировки основных определений.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
Наибольшее и наименьшее значение функции на открытом интервале
Наибольшее и наименьшее значение функции на бесконечности
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Решение:
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
Следовательно, производные функции существуют на всей области ее определения.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Квадратичная функция (ЕГЭ 2022)
Проверь себя, ответь на эти вопросы:
В конце статьи ты будешь знать ответы на эти вопросы.
Квадратичная функция — коротко о главном
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Вершина параболы: \( \displaystyle <
Квадратичная функция вида: \( y=a<
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Варианты расположения параболы в зависимости от коэффициента \( \displaystyle a\) и дискриминанта \( \displaystyle D=<^<2>>-4ac\).
Что такое функция?
Не знаешь? Тогда сперва прочитай тему «Функции» – она несложная, но очень важная.
А мы пока повторим.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»? Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции».
Все дело в понятии «область определения»:
Для некоторых функций не все аргументы можно подставить в зависимость.
Например, для функции \( y=\sqrt
Кстати, а с линейной функцией ты уже дружишь? Про нее все написано в теме «Линейная функция» – там ты поймешь, что в функциях ничего страшного нет и научишься понимать и использовать коэффициенты (это циферки перед буквой \( x\)).
И еще, надеюсь, ты умеешь решать квадратные уравнения? Освежить память можно, почитав тему «Квадратные уравнения».
Квадратичная функция — подробнее
Квадратичная функция – это функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (они и называются коэффициентами).
Число \( a\) называют старшим или первым коэффициентом такой функции, \( b\) – вторым коэффициентом, а \( c\) – свободным членом.
Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений\( E\left( y \right)\).
Какими могут быть значения аргумента квадратичной функции \( y=a<
Значит, область определения – все действительные числа:
А теперь множество значений. Все ли значения может принимать функция?
Достаточно рассмотреть самую простую квадратичную функцию \( y=<
\), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю.
Значит, эта функция всегда не меньше нуля.
А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше.
Таким образом, можем написать для \( y=<
В каждом отдельном случае область значений будет разная, но всегда – ограниченная.
График квадратичной функции
Наверняка ты слышал, что график квадратичной функции называется параболой. Как она выглядит? Сейчас нарисуем
Кстати мы очень подробно разобрали как быстро и правильно рисовать параболу. Переходи по ссылке и всему научишься.
Начнем с простейшей квадратичной функции – \( y=<
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Нарисуем эти точки на координатной плоскости и соединим их плавной линией:
Именно так и выглядит парабола. Самая нижняя ее точка называется вершиной, а части спарва и слева от вершины называем ветвями параболы. Как видим, ветви симметричны относительно вертикали, проходящей через вершину.
Рассмотрим теперь другую функцию: \( y=<
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
Сравним два рисунка.
Видно, что это как будто одна и та же парабола, просто расположенная в разных местах.
Во второй параболе вершина переместилась в точку \( \left( 1;-4 \right)\), а ветви переехали вместе с ней.
Да, так оно и есть: все параболы с одинаковым старшим коэффициентом, a выглядят одинаково – даже при разных остальных коэффициентах.
Кстати, если хочешь научиться быстро и правильно рисовать график квадратичной функции, то переходи по ссылке, там отличная статья.
Коэффициенты квадратичной функции
Давай разберем, на что влияют коэффициенты квадратичной функции.
Начнем со старшего коэффициента.
Будем рассматривать функции вида \( y=a<
Что ты видишь? Чем они отличаются? Какую закономерность можно заметить?
Во-первых, это невозможно не заметить, если \( \displaystyle \mathbf \mathbf<0>\) – вверх.
Значит, если парабола пересекает ось \( \displaystyle Ox\) в двух точках, то у нас два корня квадратного уравнения.
Если не пересекает – корней нет.
Но бывает ведь, что дискриминант уравнения равен нулю, и тогда только один корень. В этом случае парабола касается оси \( \displaystyle Ox\) вершиной:
А что такое вершина параболы?
Вершина параболы
Корень уравнения в этом случае указывает на вершину параболы. Если вспомнить формулу корня квадратного уравнения при \( \displaystyle D=0\), получим формулу вершины:
Это тоже бывает очень полезно.
Итак, всего возможны шесть разных вариантов расположения параболы. Вот они все на одном рисунке:
А теперь порешаем задачки.
Решение задач
1. График какой из функций избражен на рисунке?
2. Найдите сумму корней квадратного уравнения \( a<
3. Найдите произведение корней квадратного уравнения \( a<
4. По графику функции \( y=<
Решения
1. Первое: куда «смотрят» ветви параболы? Вниз. А что это значит? Правильно, \( \displaystyle a
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.