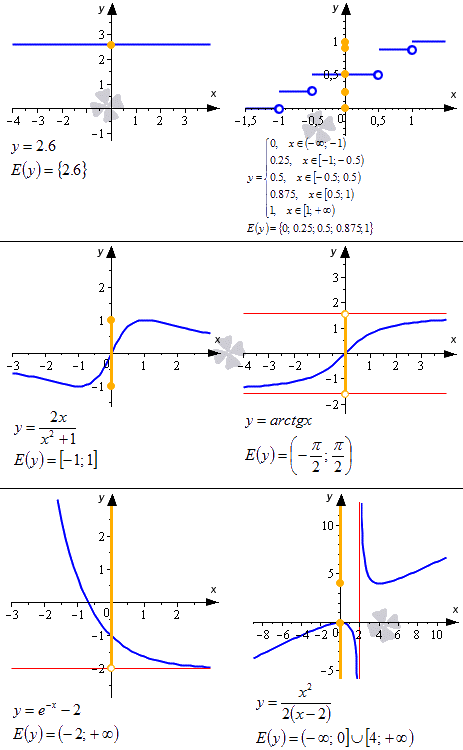
Что значит найти множество значений функции
Инструменты пользователя
Инструменты сайта
Боковая панель
Математика:
Контакты
Содержание
Нахождение множества значений функции
Обозначения
Способы нахождения областей значений функций.
Рассмотрим некоторые из них.
Используя производную
Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).
В случае, если нужно найти множества значений функции на отрезке:
Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.
Метод границ/оценок
Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Свойства непрерывной функции
Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Последовательное нахождение значений сложных аргументов функции
Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция
Области значений основных элементарных функций
| Функция | Множество значений |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^<2n>$ | E(y) = [0;+∞) |
| $y = x^<2n +1>$ | E(y) = (-∞;+∞) |
| $y = k/x$ | E(y) = (-∞;0)u(0;+∞) |
| $y = x^<\frac<1><2n>>$ | E(y) = [0;+∞) |
| $y = x^<\frac<1><2n+1>>$ | E(y) = (-∞;+∞) |
| $y = a^ | E(y) = (0;+∞) |
| $y = \log_ | E(y) = (-∞;+∞) |
| $y = \sin | E(y) = [-1;1] |
| $y = \cos | E(y) = [-1;1] |
| $y = <\rm tg>\, x$ | E(y) = (-∞;+∞) |
| $y = <\rm ctg>\, x$ | E(y) = (-∞;+∞) |
| $y = \arcsin | E(y) = [-π/2; π/2] |
| $y = \arccos | E(y) = [0; π] |
| $y = <\rm arctg>\, x$ | E(y) = (-π/2; π/2) |
| $y = <\rm arcctg>\, x$ | E(y) = (0; π) |
Примеры
Найдите множество значений функции:
Используя производную
НЕ используя производную
Найдите наибольшее и наименьшее значения функции:
Если решать эту задачу с помощью производных, то потребуется преодолевать препятствия, связанные с тем, что функция f(x) определена не на отрезке, а на всей числовой прямой.
Используя метод границ/оценок
Так как данная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением на всей области определения, если таковые существуют.
Следовательно, E(y) = [-6;6].
Используя непрерывную функцию
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
И последовательно найдём множества значений её сложных аргументов:
Используем прием, основанный на графическом изображении функции.
После преобразований функции, имеем: y 2 + x 2 = 25, причем y ≥ 0, |x| ≤ 5.
При этих ограничениях графиком данного уравнения является верхняя полуокружность с центром в начале координат и радиусом, равным 5. Очевидно, что E(y) = [0; 5].
Множество значений функции
Вы будете перенаправлены на Автор24
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Рисунок 1. Определение множества значений функции графическим методом
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
Готовые работы на аналогичную тему
Метод нахождения области значения функции через производную
Рассмотрим пример нахождения области значений функции через производную.
Теперь найдём производную функции:
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Определите область значений функции:
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
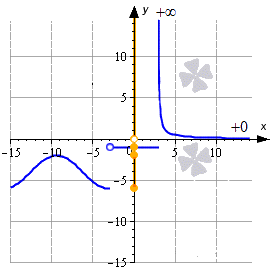
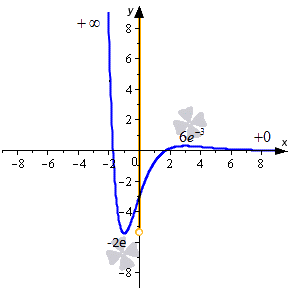
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Рассмотрим основные способы нахождения области значений функции.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Решение
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
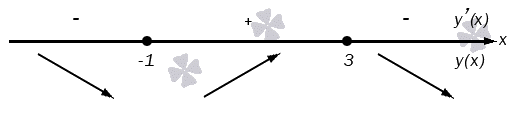
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
Решение
Решение
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
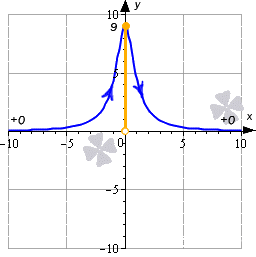
Посмотрим, как же ведет себя функция на бесконечности:
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
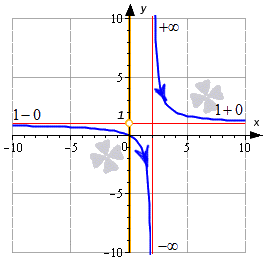
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Решение
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Решение
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Решение
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Решение
Решение показано на графике:
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
Теперь найдем соответствующие значения функции:
Посмотрим на поведение функции на бесконечности:
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Область значения функций в задачах ЕГЭ
Разделы: Математика
Понятие функции и всё, что с ним связано, относится к традиционно сложным, не до конца понятым. Особым камнем преткновения при изучении функции и подготовке к ЕГЭ являются область определения и область значений (изменения) функции.
Нередко учащиеся не видят разницы между областью определения функции и областью её значений.
И если задачи на нахождение области определения функции учащимся удаётся освоить, то задачи на нахождение множества значений функции вызывают у них немалые затруднения.
Цель данной статьи: ознакомление с методами нахождения значений функции.
В результате рассмотрения данной темы был изучен теоретический материал, рассмотрены способы решения задач на нахождение множеств значений функции, подобран дидактический материал для самостоятельной работы учащихся.
Данная статья может быть использована учителем при подготовке учащихся к выпускным и вступительным экзаменам, при изучении темы “Область значения функции” на факультативных занятиях элективных курсах по математике.
I. Определение области значений функции.
Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.
Напомним области значений основных элементарных функций.
| Функция | Множество значений |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x 2n | E(y) = [0;+∞) |
| y = x 2n +1 | E(y) = (-∞;+∞) |
| y = k/x | E(y) = (-∞;0)u(0;+∞) |
| y = x 1/2n | E(y) = [0;+∞) |
| y = x 1/2n+1 | E(y) = (-∞;+∞) |
| y = a x | E(y) = (0;+∞) |
| y = logax | E(y) = (-∞;+∞) |
| y = sin x | E(y) = [-1;1] |
| y = cos x | E(y) = [-1;1] |
| y = tg x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2 ; π/2] |
| y = arcos x | E(y) = [0; π] |
| y = arctg x | E(y) = (-π/2 ; π/2) |
| y = arcctg x | E(y) = (0; π) |
II. Свойства функций, используемые при нахождении области значений функции
Для успешного нахождения множества значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения, области значений и характер монотонности. Приведём свойства непрерывных, монотонных дифференцируемых функций, наиболее часто используемые при нахождении множества значений функций.
Свойства 2 и 3, как правило, используются вместе свойством элементарной функции быть непрерывной в своей области определения. При этом наиболее простое и краткое решение задачи на нахождение множества значений функции достигается на основании свойства 1, если несложными методами удаётся определить монотонность функции. Решение задачи ещё упрощается, если функция, вдобавок, – чётная или нечётная, периодическая и т.д. Таким образом, при решении задач на нахождение множеств значений функции следует по мере надобности проверять и использовать следующие свойства функции:
Несложные задачи на нахождение множества значений функции в большинстве своём ориентированны:
б) на выделение полного квадрата: х 2 – 4х + 7 = (х – 2) 2 + 3;
в) на преобразование тригонометрических выражений: 2sin 2 x – 3cos 2 x + 4 = 5sin 2 x +1;
г) использование монотонности функции x 1/3 + 2 x-1 возрастает на R.
III. Рассмотрим способы нахождения областей значений функций.
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Раскроем суть этих методов на конкретных примерах.
Пример 1. Найдите область значений E(y) функции y = log0,5(4 – 2·3 x – 9 x ).
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
y = log0,5(5 – (1 + 2·3 x – 3 2x )) = log0,5(5 – (3 x + 1) 2 )
И последовательно найдём множества значений её сложных аргументов:
E(3 x ) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2 ) = (-∞;4)
Пример 2. Найдите область значений функции
Решим этот пример методом оценок, суть которого состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Пример 3. Найдите область значений E(f) функции f(x) = cos2x + 2cosx.
По формуле косинуса двойного угла преобразуем функция f(x) = 2cos 2 x + 2cosx – 1 и обозначим t = cosx. Тогда f(x) = 2t 2 + 2t – 1. Так как E(cosx) =
[-1;1], то область значений функции f(x) совпадает со множеством значений функции g(t) = 2t 2 + 2t – 1 на отрезке [-1;1], которое найдём графическим методом. Построив график функции y = 2t 2 + 2t – 1 = 2(t + 0,5) 2 – 1,5 на промежутке [-1;1], находим E(f) = [-1,5; 3].
Замечание – к нахождению множества значений функции сводятся многие задачи с параметром, связанные, в основном, с разрешимостью и числом решений уравнения и неравенств. Например, уравнение f(x) = а разрешимо тогда и только тогда, когда
a 

Пример 4. При каких значениях параметра а уравнение (x + 5) 1/2 = a(x 2 + 4) имеет единственный корень на отрезке [-4;-1].
На отрезке [-4;-1] функция y = xІ + 4 непрерывна, убывает и положительна, поэтому функция g(x) = 1/(x 2 + 4) непрерывна и возрастает на этом отрезке, так как при делении на положительную функцию характер монотонности функции меняется на противоположный. Функция h(x) = (x + 5) 1/2 непрерывна и возрастает в своей области определения D(h) = [-5;+∞) и, в частности на отрезке [-4;-1], где она, кроме того, положительна. Тогда функция f(x)=g(x)·h(x), как произведение двух непрерывных, возрастающих и положительных функций, также непрерывна и возрастает на отрезке [-4;-1], поэтому её множество значений на [-4;-1] есть отрезок [f(-4); f(-1)] = [0,05; 0,4]. Следовательно, уравнение имеет решение на отрезке [-4;-1], причём единственное (по свойству непрерывной монотонной функции), при 0,05 ≤ a ≤ 0,4
Замечание. Разрешимость уравнения f(x) = a на некотором промежутке Х равносильна принадлежности значений параметра а множеству значений функции f(x) на Х. Следовательно, множество значений функции f(x) на промежутке Х совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень на промежутке Х. В частности, область значений E(f) функции f(x)совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень.
Пример 5. Найдите область значений E(f) функции
Решим пример методом введения параметра, согласно которому E(f) совпадает с множеством значений параметра а, для которых уравнение
имеет хотя бы один корень.
Так как точка а = 2 принадлежит отрезку

Как непосредственное развитие метода введения параметра при нахождении множества значений функции, можно рассматривать метод обратной функции, для нахождения которой надо решить относительно х уравнение f(x)= y, считая y параметром. Если это уравнение имеет единственное решение x =g(y), то область значений E(f) исходной функции f(x) совпадает с областью определения D(g) обратной функции g(y). Если же уравнение f(x)= y имеет несколько решений x =g1(y), x =g2(y) и т.д., то E(f) равна объединению областей определений функции g1(y), g2(y) и т.д.
Пример 6. Найдите область значений E(y) функции y = 5 2/(1-3x).
найдём обратную функцию x = log3((log5y – 2)/(log5y)) и её область определения D(x):
Так как уравнения относительно х имеет единственное решение, то
E(y) = D(x) = (0; 1)
Если область определения функции состоит из нескольких промежутков или функция на разных промежутках задана разными формулами, то для нахождения области значений функции надо найти множества значений функции на каждом промежутке и взять их объединение.
Пример 7. Найдите области значений f(x) и f(f(x)), где
Теперь, объединив промежутки [9;+∞) и [5;9] – множества значений функции f(f(x)), обозначим t = f(x). Тогда f(f(x)) = f(t), где 
Аналогично, обозначив z = f(f(x)), можно найти область значений E(f 3 ) функции f(f(f(x))) = f(z), где 5 ≤ z ≤ 9 и т.д. Убедитесь, что E(f 3 ) = [2cos8 1/2 + 7; 2cos2 + 7].
Наиболее универсальным методом нахождения множества значений функции является использование наибольшего и наименьшего значений функции на заданном промежутке.
0,5 ≤ t 3 – 2t 2 + t при 0,5 ≤ t 2 – 4t + 1. Следовательно, f(t) дифференцируема, значит, и непрерывна на отрезке [0,5;4]. Из уравнения f’(t) = 0 найдём критические точки функции t = 1/3, t = 1, первая из которых не принадлежит отрезку [0,5;4], а вторая принадлежит ему. Так как f(0,5) = 1/8, f(1) = 0, f(4) = 36, то, по свойству дифференцируемой функции, 0 – наименьшее, а 36 – наибольшее значение функции f(t) на отрезке [0,5;4]. Тогда f(t), как непрерывная функция, принимает на отрезке [0,5;4] все значения от 0 до 36 включительно, причём значение 36 принимает только при t = 4, поэтому при 0,5 ≤ t
Данная тема имеет практическое значение. В школьном курсе математики изучается тема “Область значения функции”. Такие задачи обязательно содержатся в заданиях различных математических тестов, в частности в заданиях единого государственного экзамена.
Результаты работы можно использовать на уроках и дополнительных занятиях при подготовке учащихся выпускным и вступительным экзаменам, при самостоятельной подготовке учащихся по данной теме.