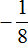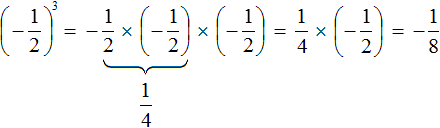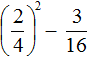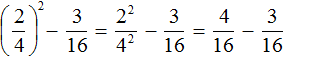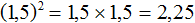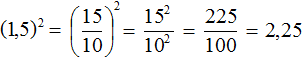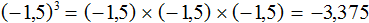Что значит натуральный показатель
натуральные показатели
Смотреть что такое «натуральные показатели» в других словарях:
Натуральные показатели — показатели, которые представляют информацию об объектах учета счетом, мерой, весом и т.п. Выбор единиц измерения зависит от особенностей объектов. Натуральные показатели используются для учета количества однородных материальных ценностей. См.… … Финансовый словарь
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ — измерители показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в физических единицах количества, веса, длины, площади, объема (в отличие от стоимостных показателей, выражаемых… … Экономический словарь
натуральные показатели — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN physical indicators … Справочник технического переводчика
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ — (см. НАТУРАЛЬНЫЕ ИЗМЕРИТЕЛИ) … Энциклопедический словарь экономики и права
Условно-натуральные показатели — показатели, которые предназначены для отражения однородных по назначению, но разных по качественным характеристикам объектов учета. См. также: Хозяйственный учет Финансовый словарь Финам … Финансовый словарь
ПОКАЗАТЕЛИ НАТУРАЛЬНЫЕ — (см. НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ) … Энциклопедический словарь экономики и права
натуральные измерители — показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в физических единицах количества, веса, длины, площади, объема (в отличие от стоимостных показателей, выражаемых в… … Словарь экономических терминов
НАТУРАЛЬНЫЕ ИЗМЕРИТЕЛИ — вид измерителей. с помощью которых получают показатели об объектах бухгалтерского учета в натуральном выражении, показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в… … Энциклопедический словарь экономики и права
ПОКАЗАТЕЛИ ЭКОНОМИЧЕСКИЕ — система численных характеристик, применяемая в анализе, учете, планировании всех областей экономической деятельности. В каждой из этих областей складывается своя система П.э., поэтому говорят о показателях плановых, показателях финансовых,… … Финансово-кредитный энциклопедический словарь
Натуральные волокна — (от лат. naturalis естественный, природный) текстильные волокна растительного, животного и минерального происхождения. Хлопок и лубяные волокна относятся к Н. В. растительного происхождения; шерсть и шёлк к волокнам животного происхождения;… … Энциклопедия моды и одежды
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ
Выбор единиц измерения зависит от особенностей объектов. Натуральные показатели используют, как правило, для учёта однородных экономических и социальных явлений в присущей им естественной форме. Урожай сельскохозяйственных культур, продукты животноводства и птицеводства, добыча нефти и газа, производство автомобилей, потребление тех или иных продуктов на душу населения, уровень безработицы, индикаторы социальной сферы и другие выражаются в натуральных показателях, поскольку их стоимостная (денежная) или какая-либо другая форма не может быть определена либо же не имеет значения для характеристики динамики и пропорций в экономике.
В условиях натурального хозяйства посредством натуральных показателей могли выражать не только количественные, но и качественные характеристики социально-экономических отношений. Так, оброк в крестьянских общинах вплоть до 1860-х годов рассчитывался в России по «силе» тех или иных хозяйств, а московские дьяки могли сосчитать, сколько «сох» (условная податная единица, применяемая для обложения землевладельческих хозяйств) содержится в рыбной «ловле», в «бортях» (промысел мёда диких пчёл), в мельницах и т. п.
Особое значение получила система натуральных показателей в условиях плановой экономики СССР и др. социалистических стран. Эти показатели служили основой определения стоимостных показателей, которые в условиях товарно-денежных отношений играли, наряду с натуральными, существенную роль. Огромное разнообразие производимых в промышленности и сельском хозяйстве продуктов требовало чёткой регламентации порядка формирования системы натуральных показателей. Обширная практика планирования и учёта продукции в натуральных показателях в советской экономике и народном хозяйстве др. стран выявили многие их (показателей) уязвимые места. Ннатуральным показателям присущи особенности, которые ограничивают область их применения. Так, каждое изделие обладает многими потребительскими свойствами, а в натуральных показателях можно отразить лишь одно из них. В отдельных случаях выход состоял в одновременном применении двух и более таких показателей. Например, выпуск двигателей планировался в штуках и единицах мощности (киловаттах).
Принято считать, что по мере развития товарно-денежных отношений система натуральных показателей уступает своё место стоимостным. Практика показывает, однако, что это происходит далеко не прямолинейно. Натурализация экономики, а потому и соответствующие ей натуральные измерители, как правило, «возвращаются» в условиях войн, кризиса финансовых систем, радикальных социальных изменений. Вместе с тем и в «спокойных» условиях рыночной экономики и национальная, и международная статистика широко использует систему натуральных показателей. Это объясняется тем, что они, в отличие от стоимостных показателей, не подвержены влиянию инфляционных процессов, на них не отражается разница валютных курсов и др. особенности, связанные со стоимостным учётом и монетарными манипуляциями. Натуральные показатели используются в демографии, при изучении социальных процессов в стране и мире, в др. социально-экономических науках.
Натуральные показатели
Смотреть что такое «Натуральные показатели» в других словарях:
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ — измерители показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в физических единицах количества, веса, длины, площади, объема (в отличие от стоимостных показателей, выражаемых… … Экономический словарь
натуральные показатели — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN physical indicators … Справочник технического переводчика
натуральные показатели — показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в физических единицах количества, веса, длины, площади, объема (в отличие от стоимостных показателей, выражаемых в… … Словарь экономических терминов
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ — (см. НАТУРАЛЬНЫЕ ИЗМЕРИТЕЛИ) … Энциклопедический словарь экономики и права
Условно-натуральные показатели — показатели, которые предназначены для отражения однородных по назначению, но разных по качественным характеристикам объектов учета. См. также: Хозяйственный учет Финансовый словарь Финам … Финансовый словарь
ПОКАЗАТЕЛИ НАТУРАЛЬНЫЕ — (см. НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ) … Энциклопедический словарь экономики и права
натуральные измерители — показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в физических единицах количества, веса, длины, площади, объема (в отличие от стоимостных показателей, выражаемых в… … Словарь экономических терминов
НАТУРАЛЬНЫЕ ИЗМЕРИТЕЛИ — вид измерителей. с помощью которых получают показатели об объектах бухгалтерского учета в натуральном выражении, показатели экономической деятельности, производства и потребления домашних хозяйств, предприятий, государства, выраженные в… … Энциклопедический словарь экономики и права
ПОКАЗАТЕЛИ ЭКОНОМИЧЕСКИЕ — система численных характеристик, применяемая в анализе, учете, планировании всех областей экономической деятельности. В каждой из этих областей складывается своя система П.э., поэтому говорят о показателях плановых, показателях финансовых,… … Финансово-кредитный энциклопедический словарь
Натуральные волокна — (от лат. naturalis естественный, природный) текстильные волокна растительного, животного и минерального происхождения. Хлопок и лубяные волокна относятся к Н. В. растительного происхождения; шерсть и шёлк к волокнам животного происхождения;… … Энциклопедия моды и одежды
Натуральные показатели
Спасибо инвесторам из Азино 777
НАТУРАЛЬНЫЕ ПОКАЗАТЕЛИ — показатели, характеризующие величины явлений в присущей им натуральной форме; измеряются в единицах, отражающих физическое состояние явлений. Так, добыча нефти в натуральном выражении измеряется в единицах массы или объема, потребление сахара на душу населения — в килограммах, валовой сбор зерна — в тоннах или центнерах, выпуск легковых автомобилей — в штуках и т, д. Натуральные показатели продукции характеризуют производство, накопление и движение потребительных стоимостей. В расчете на единицу продукции в натуральном выражении определяются затраты труда и средств, в натуре характеризуется состав основных и оборотных фондов, производственные мощности, нормы выработки и др.
Применяемые для измерения натуральных показателей физические единицы должны соответствовать принятым в международной системе единиц СИ. Натуральные показатели служат основой определения стоимостных показателей, которым в условиях товарно-денежных отношений наряду с натуральными показателями принадлежит важная роль. Огромное разнообразие производимых в промышленности и сельском хозяйстве продуктов требует четкой регламентации порядка формирования натуральных показателей.
Для обеспечения единства в планировании и учете продукции в натуральном выражении, а также возможности широкого применения в расчетах ЭВМ Госпланом СССР совместно с Госстандартом разработан единый общесоюзный классификатор продукции, содержащий наименования изделий, распределение их по классам, подклассам, группам, подгруппам и видам, а также присвоенное каждому виду продукции цифровое обозначение десятизначного кода. Натуральные показатели просты и удобны для применения в планировании и учете, для оценки итогов социалистического соревнования, они свободны от влияния многих факторов, не зависящих от качества деятельности трудовых коллективов.
В то же время натуральные показатели характеризуются такими особенностями, которые ограничивают область их применения: каждое изделие обладает многими потребительскими свойствами, а натуральные показатели отражают лишь одно из них, наиболее важное. В отдельных случаях выход из положения состоит в одновременном применении двух натуральных показателей. Например, выпуск двигателей планируется в штуках и единицах мощности (киловаттах).
Однако многие изделия обладают не одним-двумя, а несколькими важными свойствами. Скажем, для металлорежущего станка важна мощность, точность, долговечность, надежность, степень автоматизации и др. В последние годы проведена значительная работа по совершенствованию натуральных измерителей продукции. Она ориентирует предприятия на более полное удовлетворение общественных потребностей с меньшими затратами труда, позволяет лучше отражать потребительские свойства и назначение изделий. Так, производство бумаги планируется теперь не в тоннах, как раньше, а в квадратных метрах, что ориентирует на лучшее использование сырья, повышение качества бумаги.
В производстве проката наряду с физическими на первое место поставлены условные тонны, учитывающие не только массу, но и сложность, трудоемкость производства проката разного профиля и толщины. Объективное противоречие менаду способностью натуральных показателей отражать какое-либо одно свойство продукта и заинтересованностью потребителей в отражении нескольких его свойств смягчается, правильным сочетанием натуральных показателей со стоимостными. Необходимость такого сочетания определяется также тем, что в натуральном выражении, как правило, нельзя определить общий объем производства на предприятии, в объединении, отрасли или районе из-за разнообразия выпускаемых продуктов.
Источник: Краткий экономический словарь, М., 1987
 |
Обзоры и публикации |
 |
 Недавнее вступление России в ВТО вызвало массу вопросов: принесет ли членство в этой организации реальные дивиденты стране? Не приведет ли оно к ухудшению экономического положения в ряде отраслей? Поговорим об этой проблеме подробнее.
Недавнее вступление России в ВТО вызвало массу вопросов: принесет ли членство в этой организации реальные дивиденты стране? Не приведет ли оно к ухудшению экономического положения в ряде отраслей? Поговорим об этой проблеме подробнее.  Читать полностью >>
Читать полностью >> Термин оффшор прочно вошел в наш экономический лексикон. Что же представляет собой на практике регистрация компании в оффшорной зоне? Есть ли какие-либо ограничения для владельцев подобных компаний? Рассмотрим эту тему в нашем обзоре.
Термин оффшор прочно вошел в наш экономический лексикон. Что же представляет собой на практике регистрация компании в оффшорной зоне? Есть ли какие-либо ограничения для владельцев подобных компаний? Рассмотрим эту тему в нашем обзоре.  Венчурные инвестиции – занятие в высшей степени рискованное, но тем не менее в последние годы к этому вопросу приковано повышенное внимание. Чем же так привлекательно вложение в рискованные ценные бумаги или предприятия? Постараемся ответить на этот вопрос.
Венчурные инвестиции – занятие в высшей степени рискованное, но тем не менее в последние годы к этому вопросу приковано повышенное внимание. Чем же так привлекательно вложение в рискованные ценные бумаги или предприятия? Постараемся ответить на этот вопрос.  Термин хеджирование не так часто, как другие, встречается в экономической литературе, однако знание основных моментов, связанных с хеджированием, необходимо и рядовому участнику товарной биржи или фьючерсного рынка, и крупному инвестору. Рассмотрим подробнее эту тему.
Термин хеджирование не так часто, как другие, встречается в экономической литературе, однако знание основных моментов, связанных с хеджированием, необходимо и рядовому участнику товарной биржи или фьючерсного рынка, и крупному инвестору. Рассмотрим подробнее эту тему. 
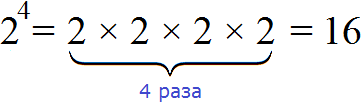
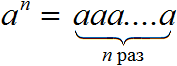
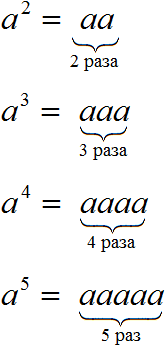
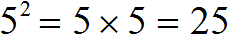

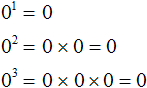
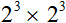
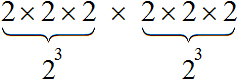
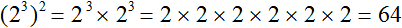

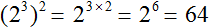

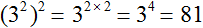
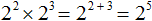


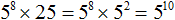
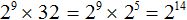
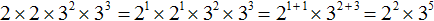

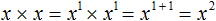
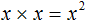
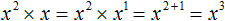
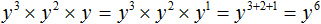
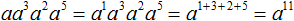
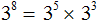
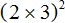
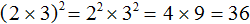
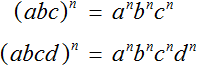
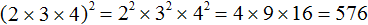


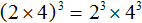
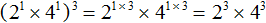
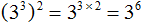
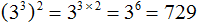

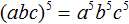
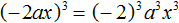
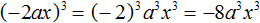
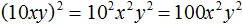
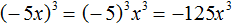
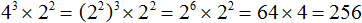
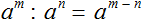
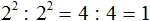
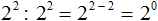
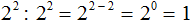
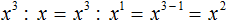
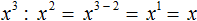
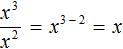

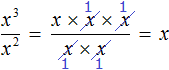

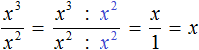


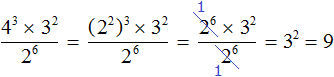

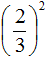
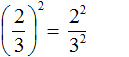
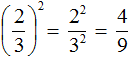
 .
.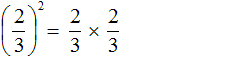
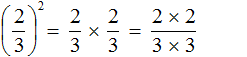
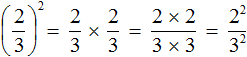
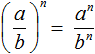
 в третью степень
в третью степень
 во вторую степень:
во вторую степень: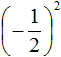
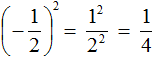
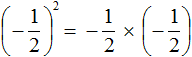
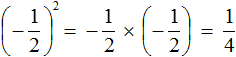
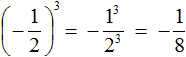
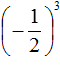 представляет собой произведение трёх множителей, каждый из которых равен дроби
представляет собой произведение трёх множителей, каждый из которых равен дроби 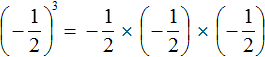
 , но затем умножив
, но затем умножив