Что значит хотя бы один

17.04.202220.04.2022 admin 0 Comments

Решение задач с формулировкой «хотя бы один»

Поговорим о задачах, в которых встречается фраза «хотя бы один». Наверняка вы встречали такие задачи в домашних и контрольных работах, а теперь узнаете, как их решать. Сначала я расскажу об общем правиле, а потом рассмотрим частный случай независимых событий и схемы Бернулли, выпишем формулы и примеры для каждого.

Общая методика и примеры

Общая методика для решения задач, в которых встречается фраза «хотя бы один» такая:

А теперь разберем ее на примерах. Вперед!

Пример 1. В ящике находится 25 стандартных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трёх наудачу выбранных деталей окажется хотя бы одна бракованная?

Действуем прямо по пунктам.
1. Записываем событие, вероятность которого надо найти прямо из условия задачи:
$A$ =(Из 3 выбранных деталей хотя бы одна бракованная).

Для первого примера запишем решение подробно, далее будем уже сокращать (а полные инструкции и калькуляторы вы найдете по ссылке выше).

4. Тогда искомая вероятность:

Пример 2. Из колоды в 36 карт берут наудачу 6 карт. Найти вероятность того, что среди взятых карт будут: хотя бы две пики.

4. Тогда искомая вероятность:

Пример 3. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета.

4. Искомая вероятность:

Частный случай. Независимые события

Идем дальше, и приходим к классу задач, где рассматривается несколько независимых событий (стрелки попадают, лампочки перегорают, машины заводятся, рабочие болеют с разной вероятностью каждый и т.п.) и нужно «найти вероятность наступления хотя бы одного события». В вариациях это может звучать так «найти вероятность, что хотя бы один стрелок из трех попадет в цель», «найти вероятность того, что хотя бы один автобус из двух вовремя приедет на вокзал», «найти вероятность, что хотя бы один элемент в устройстве из четырех элементов откажет за год» и т.д.

Если в примерах выше речь шла о применении формулы классической вероятности, здесь мы приходим к алгебре событий, используем формулы сложения и умножения вероятностей (небольшая теория тут).

Пример 4. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Действуем аналогично. Рассмотрим основное событие
$A$ =(Формула содержится хотя бы в одном справочнике). Введем независимые события:
$A_1$ = (Формула есть в первом справочнике),
$A_2$ = (Формула есть во втором справочнике),
$A_3$ = (Формула есть в третьем справочнике).

Пример 6. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Думаю, вы уже уловили принцип решения, вопрос только в количестве событий, но и оно не оказывает влияния на сложность решения (в отличие от общих задач на сложение и умножение вероятностей). Только будьте внимательны, вероятности указаны для «потребует внимания», а вот вопрос задачи «хотя бы один станок НЕ потребует внимания». Вводить события нужно такие же, как и основное (в данном случае, с НЕ), чтобы пользоваться общей формулой (1).

Ответ: 0,982. Почти наверняка мастер будет отдыхать всю смену;)

Частный случай. Повторные испытания

Думаете, дальше будет сложнее? Напротив, случаи все более частные, решения и формулы все более простые.

Подробнее о схеме Бернулли можно прочитать в онлайн-учебнике, а также посмотреть статьи-калькуляторы о решении различных подтипов задач (о выстрелах, лотерейных билетах и т.п.). Ниже же будут разобраны задачи только с «хотя бы один».

Пример 7. Пусть вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,9. Найти вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта.

Пример 8. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Думаю, с применением формулы (2) все более чем ясно (не забудьте почитать и о других задачах, решаемых в рамках схемы Бернулли, ссылки были выше). А ниже я приведу чуть более сложную задачу. Такие задачи встречаются пореже, но и их способ решения надо усвоить. Поехали!

Пример 9. Производится n независимых опытов, в каждом из которых некоторое событие A появляется с вероятностью 0,7. Сколько нужно сделать опытов для того, чтобы с вероятностью 0,95 гарантировать хотя бы одно появление события A?

Округляя, получаем что нужно провести не менее 3 опытов.

Ответ: минимально нужно сделать 3 опыта.

Полезные ссылки

Источник

хотя бы (один) раз

Смотреть что такое «хотя бы (один) раз» в других словарях:

Один день Ивана Денисовича — Щ 854 Жанр: рассказ (повесть) Автор: Александр Солженицын Язык оригинала: русский Год написания: 1959 … Википедия

Один день Ивана Денисовича (рассказ) — Один день Ивана Денисовича Автор: Александр Солженицын Жанр: повесть Язык оригинала: русский … Википедия

РАЗ — РАЗ, рас, рос, разо, предл. слитный, означающий: а) окончанье действия, как вообще все предлоги: рассмешить, разбудить; б) деленье, особленье, разноту: разломать, раздать, раскусить, разогнать; в уничтоженье, переделку снова: развить, растить;… … Толковый словарь Даля

Один против всех — Логотип … Википедия

Один против всех (телеигра, ТВЦ) — Один против всех Логотип передачи Жанр Телевизионная игра Производство Ведущий Александр Нуждин Композитор Groove Addicts, Anthony Philips Страна производства … Википедия

ОДИН — одна, одно, числит. колич. (склонение см. § 59). 1. только ед. ч. м. р. Название числа 1. Помножить один на три. Прибавить три к одному. 2. только ед. (мн. возможно при сущ., употр. только во мн. ч., а также при мн. ч. сущ. в знач. “пара”).… … Толковый словарь Ушакова

один — одна, одно, числит. колич. (склонение см. § 59). 1. только ед. ч. м. р. Название числа 1. Помножить один на три. Прибавить три к одному. 2. только ед. (мн. возможно при сущ., употр. только во мн. ч., а также при мн. ч. сущ. в знач. “пара”).… … Толковый словарь Ушакова

Один — Один ♦ Un Первый элемент перечисления (ноль, изобретенный гораздо позже, служит не для перечисления, а для счета). Может обозначать единицу (как один из элементов возможного множества; тогда мы говорим «один из…»), а также единственность… … Философский словарь Спонвиля

Один дома 2: Потерянный в Нью-Йорке — Home Alone 2: Lost in New York … Википедия

Раз в неделю — Ранняя заставка программы Жанр Юмористическая программа Автор(ы) Р. Кривицкий, В. Неклюдов, Ю. Исаков, В. Антонов, К Наумочкин, И. Осипов, А. Каранович … Википедия

Источник

Вероятность появления хотя бы одного события

$P\left( A \right) = 1 — P\left( <\bar A>\right) = 1 — \cdot\cdot \ldots \cdot$

где q — вероятность наступления события, противоположного событию A

Пример 1
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
q₁ — вероятность неисправности первого платёжного автомата;
q₂ — вероятность неисправности второго платёжного автомата.
Искомая вероятность равна:

P=1–0.02·0.02=0.9996

Пример 2

Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

Решение

А — «стрелки получат приз». Из условия задачи вероятность попадания равна р=0.3, следовательно вероятность их промаха

q=1–р=1–0,3=0,7

Отсюда искомая вероятность равна

P(A)=1–q 4 =1–0,7 4 =

=1–0,2401=0,7599

Пример 3
Вероятность попадания при одном выстреле в мишень 0,7. Найдите вероятность хотя бы одного попадания при 4 выстрелах.
Решение

q=1–р=1–0,7=0,3

P(A)=1–q 4 =1–0,3 4 =

=1–0,0081=0,9919

Пример 4
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение
А — «устройство не работает»
A₁ — «отказал первый элемент»
A₂ — «отказал второй элемент»
Найдём вероятности безотказной работы независимых элементов
q₁=1-0,05=0,95,
q₂=1-0,08=0,92
Следовательно, вероятность того, что устройство не работает равна

==1-0,874=0,126

Пример 6

Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,5; 0,6

Решение

A₁=0.3, A₂=0.4, A₃=0.5, A₄=0.6 из условия задачи.
Воспользуемся формулой:

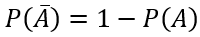
Находим соответствующие им вероятности

Р($\overline <>$) = 1 — 0,4 = 0,6

Р($\overline <>$) = 1 — 0,5 = 0,5

Р($\overline <>$) = 1-0,6 = 0,4

Из условия задачи события A₁, A₂, A₃ и A₄ независимы, следовательно получаем

Источник

Значение слова «хотя»

1. уступительный союз. То же, что хоть (в 1 знач.). И хотя [Иван Яковлевич] каждый день брил чужие подбородки, но его собственный был у него вечно не брит. Гоголь, Нос. Анатоль принес две свечки и поставил их на подоконник, хотя было уже совсем светло. Л. Толстой, Война и мир.

2. противительный союз. Употребляется для соединения противопоставляемых предложений, означает: однако, но. — Я тоже артист, хотя плохой. Тургенев, Дворянское гнездо. Начинаю понемножку оправляться от безденежья, хотя все-таки денег нет. Чехов, Письмо Н. А. Лейкину, 31 окт. 1886.

3. частица. Прост. То же, что хоть (в 4, 5 и 6 знач.). — Ну, что же? — продолжает Кошка, — Пропой, дружок, хотя немножко. И. Крылов, Кошка и Соловей. Мы не знаем даже, прочел ли Батюшков хотя одно стихотворение Пушкина. Белинский, Сочинения А. Пушкина.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

ХОТЯ’, (хоша́ обл.). 1. союз уступительный. То же, что хоть 2 в 1 знач. Одевался по-немецки и жил хотя грязненько, да открыто. Тургенев. Кто что ни говори: хотя животные, а всё-таки цари. Грибоедов. И хозяин, и хозяйка, хотя в этот час дня никогда не завтракали, однако тут и прикусили и пригубили. Тургенев. 2. союз противительный. Однако, но. Учился он порядочно, хотя часто ленился. Тургенев. Марья Алексеевна не мешала, не косилась, хотя, конечно, не оставляла без надзора. Чернышевский. 3. То же, что хоть 2 во 2, 3, 4, 5 и 6 знач. (простореч.). Мне, говорит, хотя Федот от проходных ворот, лишь бы денежки водились. А. Островский. ◊

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

хотя́ I

1. уступительный союз то же, что хоть; вводит придаточное предложение, которое описывает условие, маловероятное или неожиданное с учётом ситуации, описанной в основном предложении ◆ Но я никогда не видал, чтоб так били маленьких, и хотя здесь дядья щёлкали своих то по лбу, то по затылку, — дети относились к этому равнодушно, только почёсывая ушибленное место. Горький, «Детство», 1913–1914 г. ◆ В голом саду, за соломенным валом, пели дрозды, гудели пчёлы, хотя кое-где, среди коричневой листвы, ещё серел крепкий горбатый снежок. И. А. Бунин, «Личарда», 1913 г. (цитата из НКРЯ)

2. противительный союз вводит придаточное предложение, которое описывает условие, противоречащее ситуации, описанной в основном предложении; означает: однако, но ◆ И метафизика хочет стать наукой, походить во всем на науку, хотя это мало ей удается. Н. А. Бердяев, «Смысл творчества», 1913–1914 г. (цитата из НКРЯ) ◆ Земной шар имеет в поперечнике 12 тысяч вёрст, и хотя огромные размеры его далеко превосходят силу нашего воображения, самые длинные земные расстояния в сотни тысяч раз меньше, чем взаимные расстояния планет и Солнца. Я. И. Перельман, «Далёкие миры», 1914 г. (цитата из НКРЯ) ◆ И хотя то, что он рассказывал, было очень пустячно, но болтал он с таким неподдельным комизмом, что выходило удивительно смешно. М. П. Арцыбашев, «Миллионы», 1912 г. (цитата из НКРЯ) ◆ Кучер, урядник и Алёшка из всех сил прикидывались спокойными, хотя душа каждого из них горячо молила бога, чтобы Захар упал замертво. И. А. Бунин, «Захар Воробьёв», 1912 г. (цитата из НКРЯ)

3. прост. устар. усилительная частица по крайней мере

Источник