Что значит эпсилон в пределе
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Определение предела и число эпсилон
1. Предел последовательности.
Цитирую:
2. Геометрический смысл того же предела последовательности:
Заранее благодарен за ответ.
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось ИСН 16.02.2013, 20:14, всего редактировалось 1 раз.
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось henehen 16.02.2013, 22:34, всего редактировалось 3 раз(а).
PS. Причём, что самое интересное, такая привычка «объяснять» через левые переменные навроде эпсилонов и дельт сохраняется практически во всех учебниках и методичках, что весьма здорово способствует механическому использованию математики (не вникая ни во что) и убивает напрочь желание учиться.
И вообще, если кто-то мне объяснит человеческим языком на пальцах всю эту эпсилон-дельту технику, то я буду нечеловечески ему благодарен =)
| Заслуженный участник |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Эпсилон окрестность точки определение
Определение окрестности точки
Окрестностью действительной точки x называется любой открытый интервал, содержащий эту точку:
.
Здесь ε 1 и ε 2 – произвольные положительные числа.
Эпсилон – окрестностью точки x называется множество точек, расстояние от которых до точки x меньше ε :
.
Проколотой окрестностью точки x называется окрестность этой точки, из которой исключили саму точку x :
.
Окрестности конечных точек
В теории пределов можно использовать определение окрестности, основанное как на множестве (1), так и на множестве (2). Использование любой из этих окрестностей дает эквивалентные результаты (см. теорему ниже ⇓). Но определение (2) проще, поэтому часто используют именно эпсилон – окрестность точки, определяемую из (2).
Также широко используют понятия левосторонних, правосторонних и проколотых окрестностей конечных точек. Приводим их определения.
Проколотые окрестности конечных точек
Проколотые окрестности точки x – это те же самые окрестности, из которых исключена сама точка. Они обозначаются с кружочком над буквой. Приводим их определения.
Проколотая окрестность точки x :
.
Проколотая эпсилон – окрестность точки x :
;
.
Проколотая левосторонняя окрестность:
;
.
Проколотая правосторонняя окрестность:
;
.
Окрестности бесконечно удаленных точек
Наряду с конечными точками, также вводят понятие окрестности бесконечно удаленных точек. Все они являются проколотыми, поскольку не существует бесконечно удаленного действительного числа (бесконечно удаленная точка определяется как предел бесконечно большой последовательности).
Свойство окрестности
Также справедливы и обратные утверждения.
Эквивалентность определений предела функции по Коши
Теорема
Определения предела функции по Коши, в которых используются произвольные окрестности и окрестности с равноудаленными концами эквивалентны.
Доказательство 1 ⇒ 2
Докажем, что если число a является пределом функции по 1-му определению, то оно также является пределом и по 2-му определению.
Доказательство 2 ⇒ 1
Докажем, что если число a является пределом функции по 2-му определению, то оно также является пределом и по 1-му определению.
Это означает, что число a является пределом и по первому определению.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
ФАЗОВЫЙ ПЕРЕХОД — (фазовое превращение), в широком смысле переход в ва из одной фазы в другую при изменении внеш. условий темп ры, давления, магн. и электрич. полей и т. д.; в узком смысле скачкообразное изменение физ. св в при непрерывном изменении внеш.… … Физическая энциклопедия
Непрерывное отображение — или непрерывная функция в математике это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений. Наиболее общее определение формулируется для отображений… … Википедия
Вега — У этого термина существуют и другие значения, см. Вега (значения). Вега Звезда … Википедия
Vega — Вега Звезда Положение Веги в созвездии Лиры История исследования Обозначения Vega, α Lyr, 3 Lyr, HIP 91262[1], GCRV 11085 … Википедия
Вега (звезда) — Вега Звезда Положение Веги в созвездии Лиры История исследования Обозначения Vega, α Lyr, 3 Lyr, HIP 91262[1], GCRV 11085 … Википедия
Войти
Эпсилон-окрестности или О заключении.
В математическом анализе есть понятие эпсилон-окрестности. Если просто: берется точка, а ее эпсилон-окрестность – это все точки, находящиеся от нее на расстоянии не более эпсилон (попадающие в N-мерный шар с центром в этой точке; в случае прямой – отрезок, на плоскости – круг и т.д.). Но такая окрестность определяется не только для конечной точки. Эпсилон-окрестностью бесконечности будет «внешность» шара с центром в 0 и радиусом 1/эпсилон. Таким образом, одна и та же сфера будет ограничивать сразу два шара. И по ней не ясно, какой из этих шаров имеется ввиду.
К чему это я? А к тому, что, когда мы игнорируем кого-нибудь, отрезаем человека от себя, отводим ему пространство, и не заглядываем туда – неизвестно, кто от кого отгорожен. Пленник может быть обособлен от мира тюремной стеной, а может мыслить мир, отрезанным, отгороженным от себя. Вопрос восприятия. Отношение субъект-объект.
Если вернуться к образу заточения в бутылке забвения для определенного человека, можно взглянуть на это по-разному. В какой-то момент можно перестать мыслить себя (а значит, и быть!) пленником. Сфера-тюрьма понемногу раздвигается и становится сферой-оградой. Вроде защиты от вора. Она становится своеоброазной камерой для бывшего тюремщика (он, правда, об этом может и не догадываться). Клеточная мембрана выворачивается наизнанку, частичная проницаемость в другую сторону.
Смотрю сейчас на эти, порой бессвязные, мысли и вижу одну по сути идею. Идею диалектики, единства и борьбы противоположностей, возможно свобода. Но тут же и не-свобода – опять диалектика. Что ж, случилось прийти к этому петляющей, прерывистой, местами заросшей, но своей тропкой. Собран велосипед? Зато сборщик осознал его устройство.
Окрестность точки
Определение окрестности точки
Окрестности конечных точек
Также широко используют понятия левосторонних, правосторонних и проколотых окрестностей конечных точек. Приводим их определения.
Проколотые окрестности конечных точек
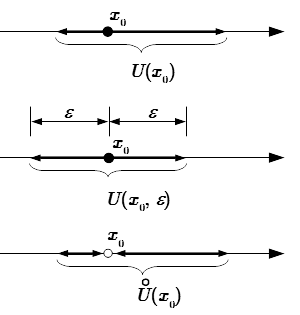
Проколотые окрестности точки x 0 – это те же самые окрестности, из которых исключена сама точка. Они обозначаются с кружочком над буквой. Приводим их определения.
Проколотая окрестность точки x 0 :
.
Проколотая эпсилон окрестность точки x 0 :
;
.
Проколотая левосторонняя окрестность :
;
.
Проколотая правосторонняя окрестность :
;
.
Окрестности бесконечно удаленных точек
Наряду с конечными точками, также вводят понятие окрестности бесконечно удаленных точек. Все они являются проколотыми, поскольку не существует бесконечно удаленного действительного числа (бесконечно удаленная точка определяется как предел бесконечно большой последовательности).
Свойство окрестности
Также справедливы и обратные утверждения.
Эквивалентность определений предела функции по Коши
Теорема
Определения предела функции по Коши, в которых используются произвольные окрестности и окрестности с равноудаленными концами эквивалентны.
Доказательство 1 ⇒ 2
Докажем, что если число a является пределом функции по 1-му определению, то оно также является пределом и по 2-му определению.
Доказательство 2 ⇒ 1
Докажем, что если число a является пределом функции по 2-му определению, то оно также является пределом и по 1-му определению.
Это означает, что число a является пределом и по первому определению.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
Что такое предел? Что такое |Xn-A| Математика Наука
Для начала успокойтесь, я понимаю на носу экзамен, но для математики нужна «холодная голова». Сейчас мы во всем разберемся, все очень просто на самом деле 🙂
Начнем с того, что вы немного запутались в обозначениях. Последовательность принято записывать в фигурных скобках:
Я допускаю, что иногда лектор (учитель) опускает фигурные скобки и обзывает последовательность просто Xn, и тут уже надо понимать из контекста, где речь идет о целой последовательности, а где о ее конкретном элементе (это не сложно, как правило).
Теперь, собственно, предел. Говорим о числовых последовательностях (для нечисловых все тоже самое, только слова другие). Так как нельзя брать предел от числа — это бессмыслица, то нет нужды писать фигурные скобки в пределе : lim
Запись, lim Xn = A, значит, что при стремлении n к бесконечности, то есть вы берете все больше и больше членов последовательности
Вот собственно и все! Теперь вы можете попробовать посмотреть, как работает это определение на простых последовательностях, например:
2)
Обратите внимание, в первом случае предел не принадлежит последовательности, а во втором — принадлежит.
Содержание
История
Кроме того, Ньютон иногда объяснял пределы в терминах, подобных определению эпсилон-дельта. [7] Готфрид Вильгельм Лейбниц разработал собственное бесконечно малое и попытался обеспечить ему прочную основу, но некоторые математики и философы все же с тревогой встретили его. [8]
Это не означает, что предельное определение было свободным от проблем, поскольку, хотя оно устраняло необходимость в бесконечно малых, оно требовало построения действительные числа от Ричард Дедекинд. [12] Это также не означает, что бесконечно малым нет места в современной математике, поскольку более поздние математики смогли строго создавать бесконечно малые величины как часть гиперреальное число или сюрреалистический номер системы. Более того, с этими величинами можно строго разрабатывать исчисления, и они имеют другие математические применения. [13]
Неофициальное заявление
Точное заявление и связанные заявления
Точная инструкция для функций с действительным знаком
Точная инструкция для функций между метрическими пространствами
Определение может быть обобщено на функции, которые отображают между метрические пространства. Эти пространства имеют функцию, называемую метрикой, которая берет две точки в пространстве и возвращает действительное число, которое представляет расстояние между двумя точками. [18] Обобщенное определение выглядит следующим образом: [19]
Отрицание точного утверждения
Точная формулировка пределов на бесконечности
Точная формулировка пределов на бесконечности выглядит следующим образом:
Также возможно дать определение в общих метрических пространствах. [ нужна цитата ]
Примеры работ
Пример 1
поскольку синус ограничена сверху 1 и снизу −1,
Пример 2
Докажем утверждение, что
Начнем с факторинга:
Таким образом, если мы далее предположим, что
Таким образом, мы установили
Пример 3
Докажем утверждение, что
Упрощение, факторинг и деление 3 в правой части импликации дает
что сразу дает требуемый результат, если мы выберем
Непрерывность
Функция ж как говорят непрерывный в c если они оба определены в c и его стоимость в c равняется пределу ж так как Икс подходы c:
Функция ж называется непрерывным на интервале я если он непрерывен в каждой точке c из я.
Сравнение с бесконечно малым определением
Учебники по исчислению бесконечно малых на основе РобинсонЭтот подход дает определения непрерывности, производной и интеграла в стандартных точках в терминах бесконечно малых. После того, как такие понятия, как непрерывность, были подробно объяснены с помощью подхода, использующего микропрерывность, также представлен эпсилон-дельта-подход. Карел Хрбачек утверждает, что определения непрерывности, производной и интеграции в нестандартном анализе в стиле Робинсона должны основываться на ε–δ метод, чтобы охватить также нестандартные значения ввода. [25] Błaszczyk et al. утверждает, что микропрерывность полезен для разработки прозрачного определения единообразной преемственности и характеризует критику Грбачека как «сомнительное причитание». [26] Грбачек предлагает альтернативный нестандартный анализ, который (в отличие от Робинсона) имеет множество «уровней» бесконечно малых, так что пределы на одном уровне могут быть определены в терминах бесконечно малых на следующем уровне. [27]