Что значит четность функции
Четные и нечетные функции
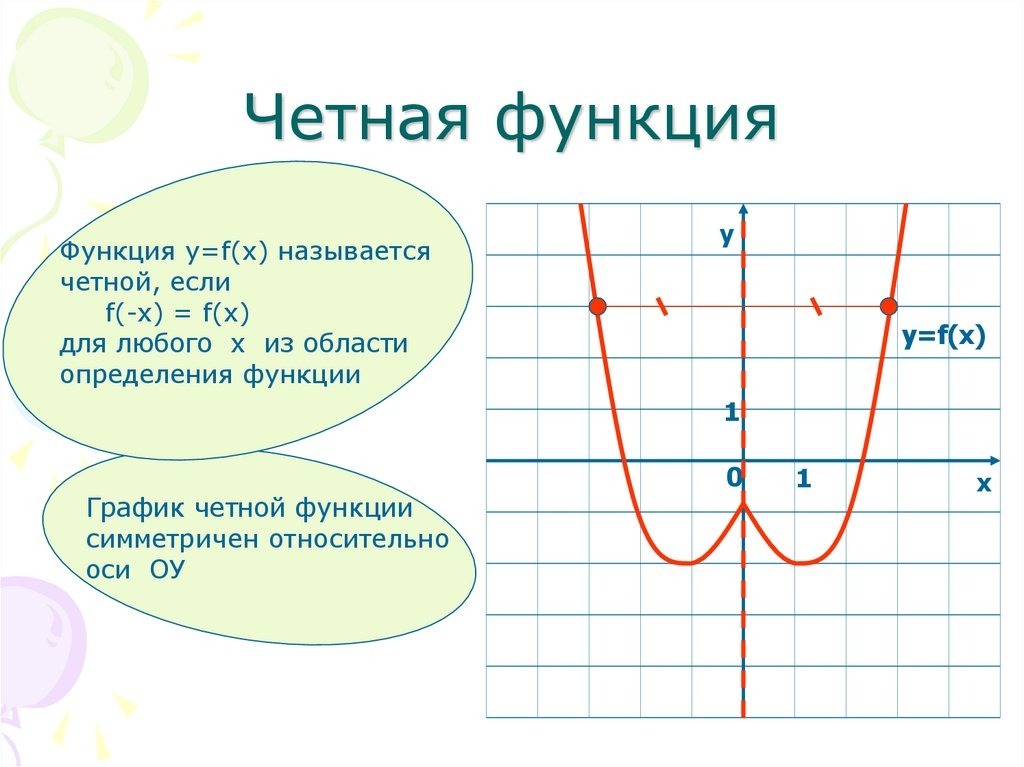
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
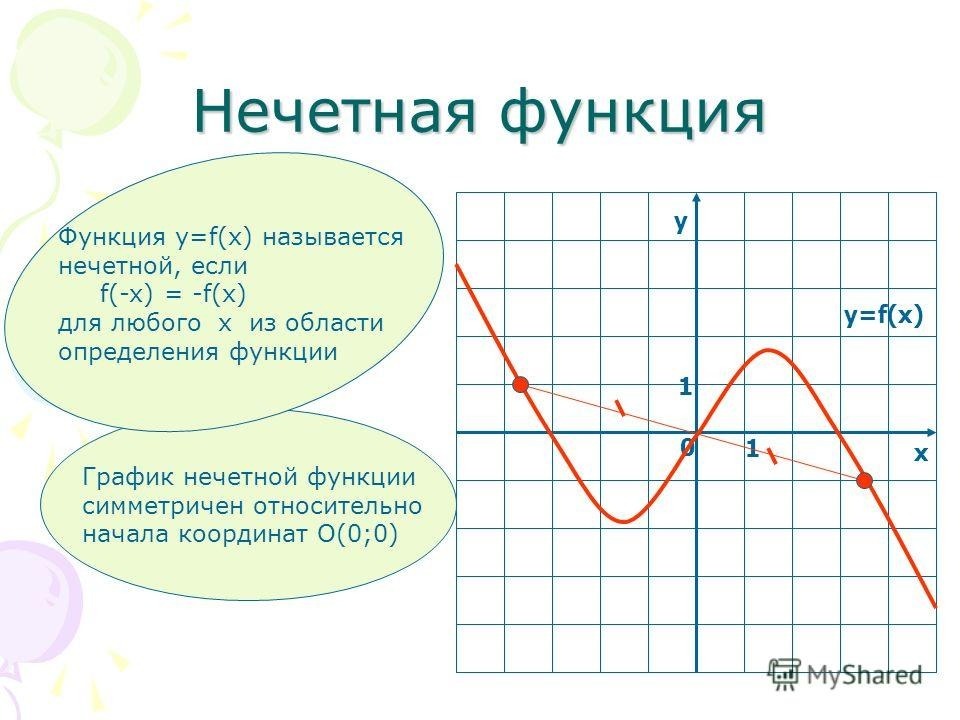
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
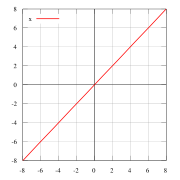
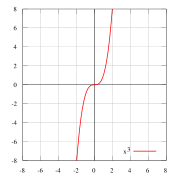
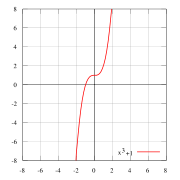
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
Чётность функции
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
Определения
Свойства
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Полезное
Смотреть что такое «Чётность функции» в других словарях:
Чётность — Чётность: В Викисловаре есть статья «чётность» Чётность в теории чисел способность целого числа делитьс … Википедия
Чётность (математика) — Чётность в теории чисел способность целого числа делиться без остатка на 2. Чётность функции в математическом анализе определяет, изменяет ли функция знак при изменении знака аргумента: для чётной/нечётной функции. Чётность в квантовой механике… … Википедия
Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия
Чётность (физика) — У этого термина существуют и другие значения, см. Чётность. Чётность свойство физической величины сохранять свой знак (или изменять на противоположный) при некоторых дискретных преобразованиях. Она выражается числом, принимающим два… … Википедия
Чётность уровня — Чётность состояния физической системы (чётность волновой функции), соответствующего данному уровню энергии. Такая характеристика уровней энергии возможна для системы частиц, между которыми действуют электромагнитные или ядерные силы,… … Большая советская энциклопедия
чётность — и; ж. к Чётный. Ч. чисел. Ч. изотопов. * * * чётность квантовое число, характеризующее симметрию волновой функции Ψ физической системы или элементарной частицы при некоторых дискретных преобразованиях; если при таком преобразовании Ψ не меняет… … Энциклопедический словарь
Исследование функции — Исследование функции задача, заключающаяся в определении основных параметров заданной функции. Содержание 1 Устаревание 2 Основные параметры 3 Источники … Википедия
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия
Нечётные и чётные функции — Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название… … Википедия
Нечетные и четные функции — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Чётные и нечётные функции
Сегодня мы разберём:
1. Определение
Примеры чётных функций:
Примеры нечётных функций:
2. Исследование функции на чётность
Чтобы узнать, является функция чётной или нечётной (или вообще общего вида), нужны две проверки:
Главное, чтобы функция была задана формулой, а не таблицей, графиком или ещё как. Тогда исследование на чётность занимает несколько секунд. Мы сейчас убедимся в этом, но сначала важное замечание.
Примеры симметричных множеств:
Примеры несимметричных множеств:
Первые два множества несимметричны всего в одной точке (кстати, какой?). Но этого достаточно, чтобы прекратить исследование и отнести функцию к общему виду.
Разберём несколько примеров. Для начала — стандартный:
Исследуйте на чётность / нечётность функцию
А вот более хитрый случай:
Исследуйте на чётность / нечётность функцию
Область определения. Перед нами рациональная дробь. Её знаменатель должен быть отличен от нуля:
\[\begin
Следовательно, область определения
Дальше попробуйте сами:
Исследуйте на чётность / нечётность функцию
Умение быстро определять чётность — чрезвычайно полезный навык. Особенно когда вы начнёте решать задачи с параметрами и всевозможные варианты ДВИ.
3. График чётной и нечётной функции
Всего два факта, которые нужно знать:
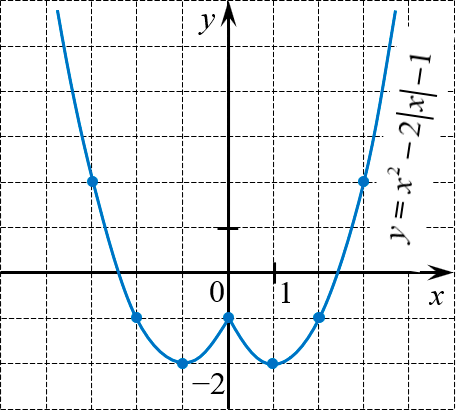
Ниже приведены графики нескольких чётных функций. Попробуйте построить их самостоятельно.
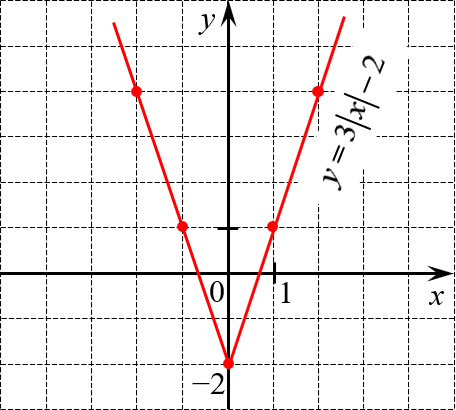
Постройте график функции
Постройте график функции
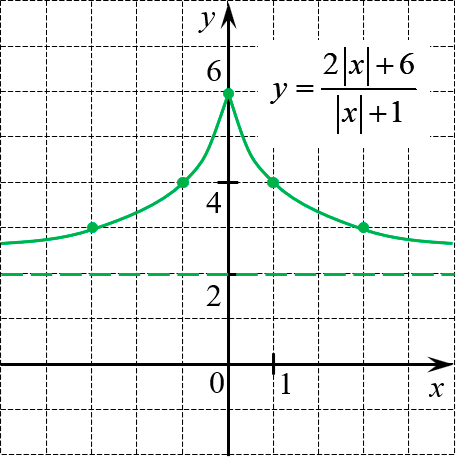
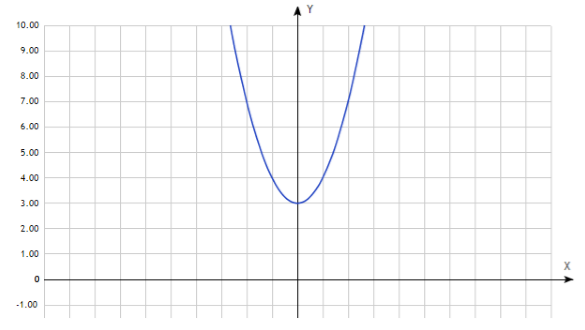
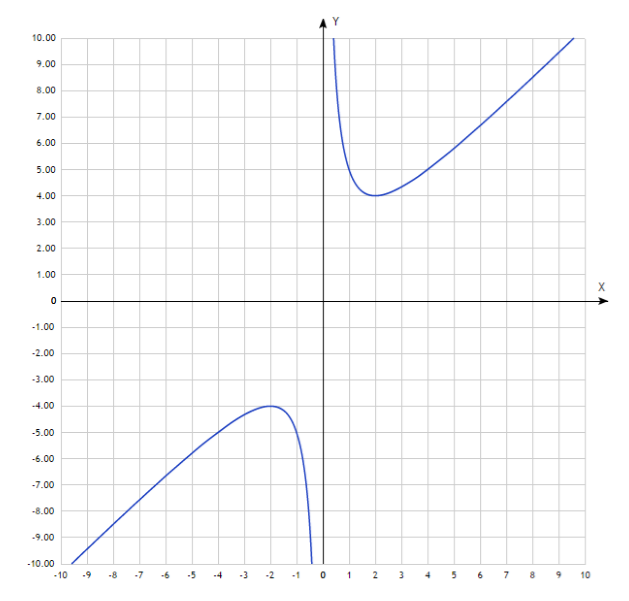
Это обычная гипербола, сдвинутая на 1 влево и на 2 вверх. Итого получим:
Обратите внимание на последний график. При всяком сдвиге и симметрии желательно показывать не только новое положение самого графика, но и положение всех ориентиров: вспомогательная система координат, вертикальные и горизонтальные асимптоты (особенно актуально для гипербол) и т.д.
Зачем всё это нужно? Исследование функции на чётность и нечётность незаменимо для решения сложных уравнений и задач с параметром:
4. Дополнение. Задачи с параметром
Чётность функций редко встречается сама по себе. Прежде всего это инструмент для решения сложных задач.
Задача решена. Ответы:
И ещё одна задача. Попробуйте решить её самостоятельно:
А чтобы действительно разобраться с чётностью, обязательно изучите ещё две темы:
После этого половина задач с параметром перестанет казаться вам сложными.:)
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
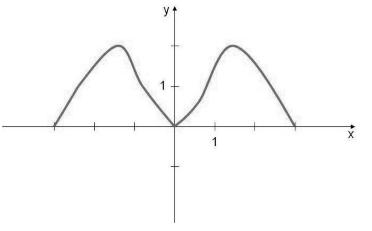
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
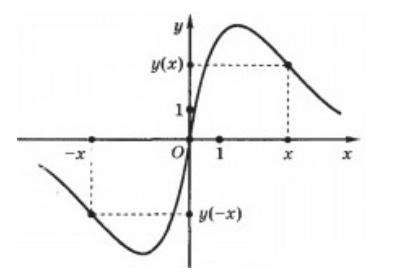
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
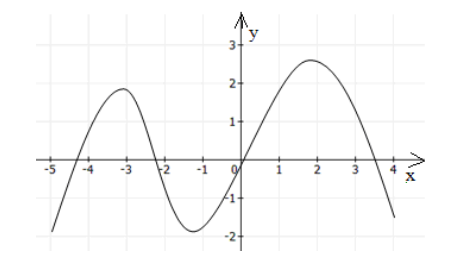
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021