Что такое xor сумма
Найти максимальную длину подмассива, XOR-сумма которого строго положительна
На зачете в параллели C были введены оригинальные правила оценки. Каждому ученику давался большой массив чисел, после чего ему надо было найти в этом массиве подмассив (несколько последовательных элементов массива) с максимальной XOR-суммой. Как всегда, есть люди, для которых главное — получить не ноль. Помогите ленивым школьникам и найдите максимальную длину подмассива, XOR-сумма которого строго положительна.
Примеры
Входные данные
6
0 0 3 7 4 0
Результат работы
4
Не могу понять что такое XOR-сумма пишу cout 0

1.Дана матрица C(M,N). Сформировать вектор В, элементами которого являются значения элементов тех.

Здравствуйте.Есть задача: Дан целочисленный массив из 20 элементов. Элементы массива могут.
Массив: Найти в массиве количество пар соседних элементов, сумма которых положительна
Дан целочисленный массив из 111 элементов. Элементы массива могут принимать целые значения от.
Найти в массиве количество пар соседних элементов, произведение которых нечётно, а сумма – положительна
Доброго времени суток, форумчане. Уезжаю до 31 числа. Возвращаюсь поздно. Времени нет. Много задач.
Чо орёшь-то? Я ещо не дочитал.
Добавлено через 2 минуты
построим таблицу истинности для функции f = x1 ^ x2, чтобы стало понятнее:
| x1 | x2 | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
xor-сумма это и есть по сути операция xor, которую еще называют сложением по модулю 2 или исключающим или. Над числами данная операция производится побитово.
Значит алгоритм такой :
Считаем сначала xor-сумму всего массива. Находим самый правый ненулевой элемент. Идем с начала массива. В i позиции убираем i-1 элемент из xor-суммы (достаточно снова сделать xor xor-суммы и этого элемента) так мы получаем xor отрезка i..n. Делаем как на пунктах 1-2. Выводим ответ.
Оператор Xor (Visual Basic)
Выполняет логическое исключение для двух Boolean выражений или побитовое исключение для двух числовых выражений.
Синтаксис
Компоненты
result
Обязательный элемент. Любая Boolean или числовая переменная. Для логического сравнения result — это логическое исключение (исключающее логическое сложение) двух Boolean значений. Для битовых операций result — это числовое значение, представляющее побитовое исключение (исключающее побитовое сложение) двух числовых битов.
expression1
Обязательный. Произвольное выражение типа Boolean или числового типа.
expression2
Обязательный. Произвольное выражение типа Boolean или числового типа.
Комментарии
| Если expression1 имеет значение | И expression2 является | Значение result равно |
|---|---|---|
| True | True | False |
| True | False | True |
| False | True | True |
| False | False | False |
При логическом сравнении Xor оператор всегда вычисляет оба выражения, которые могут включать вызовы процедур. Не существует аналога сокращенного Xor выражения, поскольку результат всегда зависит от обоих операндов. Дополнительные операторы для сокращенного вычисления логических операторов см. в разделе оператор AndAlso и оператор OrElse.
Для побитовых операций Xor оператор выполняет побитовое сравнение одинаково позиционированных битов в двух числовых выражениях и устанавливает соответствующий бит в result соответствии со следующей таблицей.
| Если бит в expression1 имеет значение | И bit в expression2 имеет | Бит в result имеет значение |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Так как логические и побитовые операторы имеют более низкий приоритет, чем другие арифметические и реляционные операторы, все битовые операции должны быть заключены в круглые скобки, чтобы обеспечить точное выполнение.
Например, 5 Xor 3 — 6. Чтобы узнать, почему это так, преобразуйте значения 5 и 3 в двоичные представления, 101 и 011. Затем используйте предыдущую таблицу, чтобы определить, что 101 Xor 011 имеет значение 110, которое является двоичным представлением десятичного числа 6.
Типы данных
если операнды состоят из одного Boolean выражения и одного числового выражения, Visual Basic преобразует Boolean выражение в числовое значение (– 1 для True и 0 для False ) и выполняет побитовую операцию.
Перегрузка
Xor Оператор можно перегрузить, что означает, что класс или структура может переопределить свое поведение, когда операнд имеет тип этого класса или структуры. Если код использует этот оператор для такого класса или структуры, убедитесь, что вы понимаете его переопределенное поведение. Для получения дополнительной информации см. Operator Procedures.
Пример 1
Пример 2
В следующем примере оператор используется Xor для выполнения логического исключения (исключающее логическое сложение) для отдельных битов двух числовых выражений. Бит в результирующем шаблоне устанавливается, если только один из соответствующих битов операндов имеет значение 1.
В предыдущем примере выдается результат 2, 12 и 14 соответственно.
Основные логические операции. AND, NOT, OR и XOR (исключающее или)
В этой статье мы поговорим о некоторых битовых операциях. Рассмотрим основные из них: XOR (исключающее ИЛИ), AND (И), NOT (НЕ) а также OR (ИЛИ).
Как известно, минимальной единицей измерения информации является бит, который хранит одно из 2-х значений: 0 (False, ложь) либо 1 (True, истина). Таким образом, битовая ячейка может одновременно находиться лишь в одном из двух возможных состояний.
Для манипуляций с битами используют определённые операции — логические или булевые. Они могут применяться к любому биту, вне зависимости от того, какое у него значение — ноль или единица. Что же, давайте посмотрим на примеры использования трёх основных логических операций.
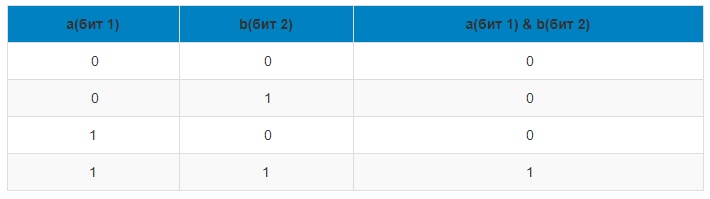
Логическая операция AND (и)
Оператор AND выполняется с 2-мя битами, возьмём, к примеру, a и b. Результат выполнения операции AND равен 1, если a и b равняются 1. В остальных случаях результат равен 0. Например, с помощью AND вы можете узнать, чётное число или нет.
Посмотрите на таблицу истинности операции AND:
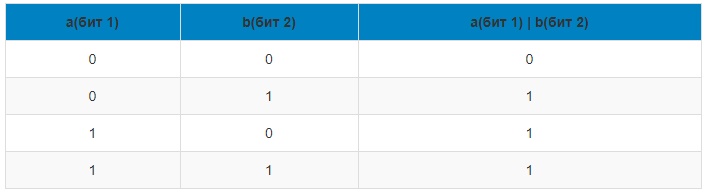
Логическая операция OR (ИЛИ)
Оператор OR также выполняется с 2-мя битами (a и b). Результат равен 0, если a и b равны 0, иначе он равен 1. Смотрим таблицу истинности.
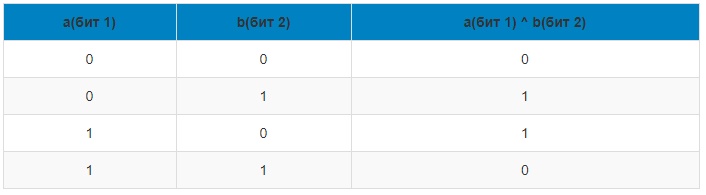
Логическая операция XOR (исключающее ИЛИ)
XOR выполняется с 2-мя битами (a и b). Результат выполнения операции XOR (исключающее ИЛИ) равен 1, когда один из битов b или a равен 1. В остальных ситуациях результат применения оператора XOR равен 0.
Таблица истинности логической операции для XOR (исключающее ИЛИ) выглядит так:
Используя XOR (исключающее ИЛИ), вы можете поменять значения 2-х переменных одинакового типа данных, не используя временную переменную. А ещё, посредством XOR можно зашифровать текст, например:
Согласен, XOR — далеко не самый надёжный метод шифрования, но это не значит, что его нельзя сделать частью какого-либо шифровального алгоритма.
Логическая операция NOT (НЕ)
Это побитовое отрицание, поэтому выполняется с одним битом и обозначается
Результат зависит от состояния бита. Если он в нулевом состоянии, то итог операции — единица и наоборот. Всё предельно просто.
Эти 4 логические операции следует запомнить в первую очередь, т. к. с их помощью можно получить практически любой возможный результат. Также существуют такие операции, как (побитовый сдвиг влево) и >> (побитовый сдвиг вправо).
Практика применения XOR в программировании
В данной статье я расскажу о битовой операции XOR (исключающее ИЛИ) и приведу наиболее интересные примеры ее применения на JAVA.
Итак, XOR – операция, которая принимает значение «истина» только если всего один из аргументов имеет значение «истина».
XOR обладает следующими свойствами:
a XOR 0 = a
a XOR a = 0
a XOR b = b XOR a
(a XOR b) XOR b = a
В языке JAVA (а также в С, С++, C#, Ruby, PHP, JavaScript) операция обозначается символом «^».
Обмен значений переменных без использования дополнительной переменной
С использованием операции XOR можно реализовать обмен значений однотипных пременных без использования дополнительной переменной:
или в более короткой записи:
Таким образом можно, например, реализовать реверс текстовой строки:
Следует, однако, заметить, что такой код не дает выигрыша в скорости по сравнению с кодом использующим временную переменную.
Шифрование
Шифрование на основе операций XOR использует свойство:
(a XOR k) XOR k = a
где k – выступает в роли ключа
Простая реализация шифрования строки:
Попробуем зашифровать строку “Съешь ещё этих мягких французских булок, да выпей чаю.” И в качестве ключа возьмем слово “хабра”:
Узким местом такого шифрования является то, что зная часть зашифрованного текста можно с легкостью восстановить ключ и, соответственно, расшифровать весь текст. Поэтому в чистом виде он редко используется на практике, хотя его применяют как часть более сложных алгоритмов шифрования.
Интересно, что в свое время данный алгоритм использовался Microsoft для шифрования содержимого документов в Office 95.
Генератор случайных чисел XORShift
В 2003 году Джордж Марсаглия представил миру быстрый алгоритм генерации случайных чисел с использованием XOR – XORShift.
Одна из возможных его рализаций:
39462749392662495
4596835458788324745
-7932128052244037525
-2502212788642280052
3288035714308340525
-8561046377475020727
-812160615072319265
-3869866974339671508
-7329504029400927428
3890915262874757420
В заключение просьба тем, у кого есть другие красивые примеры применения XOR, не вошедшие в статью, рассказать о них.
Префиксные суммы. XOR
Задачи на запросы
Префиксные суммы
В большинстве задач на запросы используется приём под названием предпросчёт. То есть ещё до начала поступления запросов нужно посчитать некоторый параметр, который поможет быстро на них отвечать. Этот принцип и лежит в основе префиксных сумм.
Идея префиксных сумм проста донельзя. Запишем сумму на отрезке \([L; R]\) в таком виде:
Этот приём может показаться очень простым, но он очень часто помогает при решении задач.
Префиксные суммы в матрицах
Префиксные суммы легко обобщаются на двухмерные, и даже многомерные массивы. Рассмотрим двухмерный случай.
Нам нужно уметь отвечать на запросы вида “найти сумму в прямоугольнике \((x_1, y_1, x_2, y_2)\)”. Разложим его на следующие запросы на “префиксах”:
Обозначим красный, зелёный, синий, и оранжевый цвета \(R, G, B, O\). Тогда предыдущая формула преобратает вид:
Сумма на “префиксе” в двухмерном варианте считается по похожим формулам:
Реализация для двухмерного варианта:
Операция XOR
\[0 \oplus 0 = 0 \\ 1 \oplus 1 = 0 \\ 0 \oplus 1 = 1 \\ 1 \oplus 0 = 1\]
То есть XOR двух битов равняется \(0\), если они совпадают, и \(1\), если отличаются.
Так как эта операция побитовая, при применении её к числам, она будет применяться отдельно к каждому биту:
\[46 \oplus 35 = 101110_2 \oplus 100011_2 = 001101_2 = 1101_2 = 13\]
Операция XOR разбирается в этой лекции из-за своего удивительного уникального свойства. Пусть \(a \oplus b = c\). Тогда, все следующие утверждения верны:
\[a \oplus b = c \\ a \oplus c = b \\ b \oplus a = c \\ b \oplus c = a \\ c \oplus a = b \\ c \oplus b = a\]
То есть эта операция обратна сама себе.
Это свойство позволяет использовать её аналогично префиксным суммам. Пусть нам нужно найти XOR всех чисел на отрезке \([L; R]\). Просто запишем его в виде:
Префиксные XOR’ы считаются абсолютно так же, как префиксные суммы. Изменив несколько символов в реализации запросов суммы на отрезке, получаем реализацию запросов XOR на отрезке:
В принципе, идея функций на префиксе применима к любой обратимой функции, но чаще всего она используется с суммой или XOR.