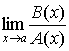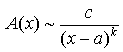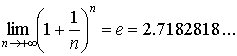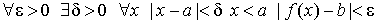Что такое supremum и infinum
В математика, то инфимум (сокращенно инф; множественное число инфима) из подмножество S из частично заказанный набор Т это величайший элемент в Т что меньше или равно всем элементам S, если такой элемент существует. [1] Следовательно, термин наибольшая нижняя граница (сокращенно GLB) также широко используется. [1]
В супремум (сокращенно Как дела; множественное число супрема) подмножества S частично упорядоченного набора Т это наименьший элемент в Т который больше или равен всем элементам S, если такой элемент существует. [1] Следовательно, супремум также называют наименьшая верхняя граница (или же LUB). [1]
Инфимум в точном смысле двойной к концепции супремума. Инфима и супрема действительные числа общие частные случаи, которые важны в анализ, и особенно в Интеграция Лебега. Однако общие определения остаются в силе и в более абстрактном контексте теория порядка где рассматриваются произвольные частично упорядоченные множества.
Содержание
Формальное определение
Нижняя граница а из S называется инфимум (или же наибольшая нижняя граница, или же встретить) из S если
Верхняя граница б из S называется супремум (или же наименьшая верхняя граница, или же присоединиться) из S если
Существование и уникальность
Инфима и супрема не обязательно существуют. Существование нижней грани подмножества S из п может потерпеть неудачу, если S не имеет вообще никакой нижней границы или если набор нижних границ не содержит наибольшего элемента. Однако, если нижняя грань или супремум существует, она уникальна.
Следовательно, частично упорядоченные множества, для которых, как известно, существуют определенные инфимы, становятся особенно интересными. Например, решетка частично упорядоченный набор, в котором все непустой конечный подмножества имеют как супремум, так и нижнюю грань, а полная решетка частично упорядоченный набор, в котором все подмножества имеют как верхнюю, так и нижнюю границу. Более подробную информацию о различных классах частично упорядоченных множеств, которые возникают из таких соображений, можно найти в статье о свойства полноты.
Если супремум подмножества S существует, он уникален. Если S содержит наибольший элемент, тогда этот элемент является супремумом; в противном случае супремум не принадлежит S (или не существует). Точно так же, если нижняя грань существует, она уникальна. Если S содержит наименьший элемент, тогда этот элемент является нижним пределом; в противном случае нижняя грань не принадлежит S (или не существует).
Отношение к максимальным и минимальным элементам
Нижняя грань подмножества S частично упорядоченного набора п, если предположить, что он существует, не обязательно принадлежит S. Если да, то это минимальный или наименьший элемент из S. Аналогично, если супремум S принадлежит S, это максимальный или наибольший элемент из S.
Однако определение максимальные и минимальные элементы более общий. В частности, в наборе может быть много максимальных и минимальных элементов, в то время как инфима и супремум уникальны.
В то время как максимумы и минимумы должны быть членами рассматриваемого подмножества, нижняя грань и верхняя грань подмножества не обязательно должны быть членами этого подмножества.
Минимальные верхние границы
Свойство с наименьшей верхней границей
В свойство с наименьшей верхней границей является примером вышеупомянутого свойства полноты что характерно для набора действительных чисел. Это свойство иногда называют Дедекиндова полнота.
Если заказанный набор S обладает тем свойством, что каждое непустое подмножество S имеющая верхнюю границу также имеет наименьшую верхнюю границу, то S говорят, что она имеет свойство наименьшей верхней границы. Как отмечалось выше, множество ℝ всех действительных чисел имеет свойство наименьшей верхней границы. Аналогично, множество integ целых чисел обладает свойством наименьшей верхней границы; если S непустое подмножество и существует некоторое число п так что каждый элемент s из S меньше или равно п, то существует точная верхняя оценка ты за S, целое число, которое является верхней границей для S и меньше или равен любой другой верхней границе для S. А хорошо организованный set также имеет свойство наименьшей верхней границы, а пустое подмножество также имеет наименьшую верхнюю границу: минимум всего набора.
Если в частично упорядоченном наборе п каждое ограниченное подмножество имеет верхнюю грань, это также относится к любому множеству Икс, в функциональном пространстве, содержащем все функции из Икс к п, куда ж ≤ грамм если и только если ж(Икс) ≤ грамм(Икс) для всех Икс в Икс. Например, это применимо к реальным функциям, и, поскольку их можно рассматривать как частные случаи функций, для реальных п-наборы и последовательности действительных чисел.
Инфима и супрема действительных чисел
В анализ, нижняя и верхняя граница подмножеств S из действительные числа особенно важны. Например, отрицательный действительные числа не имеют наибольшего элемента, и их верхняя грань равна 0 (что не является отрицательным действительным числом). [1] В полнота действительных чисел влечет (и эквивалентно), что любое ограниченное непустое подмножество S действительных чисел имеет точную нижнюю и верхнюю грань. Если S не ограничена снизу, часто формально пишут inf (S) = −∞. Если S является пустой, пишут inf (S) = +∞.
Характеристики
В тех случаях, когда нижняя и верхняя границы множеств А и B существуют следующие тождества:
Двойственность
Если обозначить через п op частично упорядоченный набор п с отношением обратного порядка, т.е.
затем точная нижняя грань подмножества S в п равен супремуму S в п op наоборот.
Примеры
Инфима
Супрема
В последнем примере супремум набора рациональные является иррациональный, что означает, что рациональные числа неполный.
Одно из основных свойств супремума:
Как дела < ж ( т ) + грамм ( т ) ∣ т ∈ А >≤ Как дела < ж ( т ) ∣ т ∈ А >+ Как дела < грамм ( т ) ∣ т ∈ А >
Супремум подмножества S из (ℕ, |), где | обозначает «разделяет», это наименьшее общее кратное элементов S.
Супремум подмножества S из (п, ⊆), где п это набор мощности некоторого множества, является супремумом по (подмножеству) подмножества S из п это союз элементов S.
1. Теория пределов
1.1 Супремум и инфимум
Определение 1. Множество < x >, элементами которого являются числа, называется числовым множеством.
Определение 2. Множество вещественных чисел < x > называется ограниченным сверху (снизу), если существует число M ( m ) такое, что 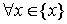
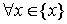
Число M называется верхней гранью числового множества < x >. Аналогично, число m называется нижней гранью числового множества < x >.
Верхних (нижних) граней бесконечно много, так как любое число, большее M (меньшее m ), есть также верхняя (нижняя) грань.
Определение 3. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества < x > (обозначение sup < x >).
Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества < x > (обозначение inf < x >).
Более точно, эти понятия выражаются следующими свойствами:
1. 
2. 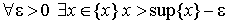
1. 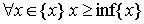
2. 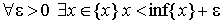
Теорема о существовании супремума и инфимума числового множества.
Если числовое множество < x > не пусто и ограничено сверху, то у него существует sup < x >.
Если числовое множество < x > не пусто и ограничено снизу, то у него существует inf < x >.
1.2 Последовательности
Определение 1. Числовой последовательностью (в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел
Обратите внимание на два момента.
1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!
2. Все числа упорядочены, то есть расположены в определенном порядке.
В дальнейшем для последовательности часто будем использовать сокращенное обозначение < xn >.
Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них.
1. Умножение последовательности на число.
Последовательность c × < xn > – это последовательность с элементами < c × xn >, то есть
2. Сложение и вычитание последовательностей.
или, более подробно,
3. Умножение последовательностей.
4. Деление последовательностей.
Естественно, предполагается, что в этом случае все yn ¹ 0.
Последовательность < xn > называется ограниченной сверху, если 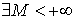
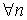
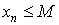
Последовательность < xn > называется ограниченной снизу, если 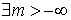
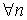
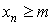
Последовательность < xn > называется ограниченной, если она одновременно ограничена и сверху и снизу.
1.3 Предел последовательности.
Основное определение. Число a называется пределом последовательности < xn > при n стремящимся к бесконечности, если
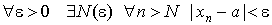
Для этого факта используют следующие обозначения:
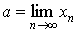
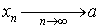
Говорят, что 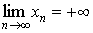
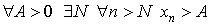
Говорят, что 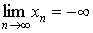
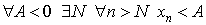
Последовательность < xn > называется бесконечно большой, если 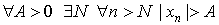
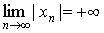
1.4 Бесконечно малые последовательности.
Оределение. Последовательность < xn > называется бесконечно малой, если 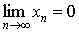

Бесконечно малые последовательности имеют следующие свойства.
1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.
2. Бесконечно малая последовательность ограничена.
3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
1.5 Сходящиеся последовательности.
Определение. Если существует конечный предел 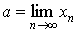
Сходящиеся последовательности имеют следующие свойства.
1. Сходящаяся последовательность ограничена.
2. 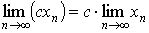
3. 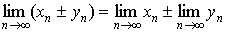
4. 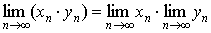
5. Если 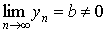
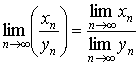
1.6 Предельный переход в неравенствах.
1. 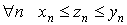
2. 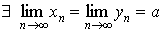
то существует 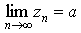
1.7 Предел монотонной последовательности.
Последовательность < xn > называется монотонно возрастающей, если для любого n xn +1 ³ xn .
Последовательность < xn > называется строго монотонно возрастающей, если для любого n xn +1 > xn .
Последовательность < xn > называется монотонно убывающей, если для любого n xn +1 £ xn .
Последовательность < xn > называется строго монотонно убывающей, если для любого n xn +1 xn .
Теорема о существовании предела монотонной последовательности.
1. Если последовательность < xn > монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup < xn > ( inf < xn > ).
На основании этой теоремы доказывается, что существует так называемый замечательный предел
1.8 Подпоследовательности
и рассмотрим последовательность 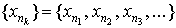
Если < xn > – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.
Лемма Больцано- Вейерштрасса.
1. Из любой ограниченной последовательности можно извлечь такую подпоследовательность, которая сходится к конечному пределу.
2. Из любой неограниченной последовательности можно извлечь бесконечно большую подпоследовательность.
На основании этой леммы доказывается один из основных результатов теории пределов –
Признак сходимости Больцано-Коши.
Для того, чтобы у последовательности < xn > существовал конечный предел, необходимо и достаточно, чтобы
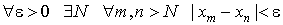
Последовательность, удовлетворяющая этому свойству, называется фундаментальной последовательностью, или последовательностью, сходящейся в себе.
1.9 Предел функции
Основное определение. Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к a (обозначение 
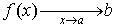
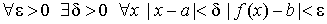
Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к + ¥ (обозначение 

Говорят, что функция f ( x ) стремится к + ¥ при x стремящимся к a (обозначение 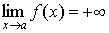
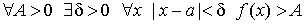
( 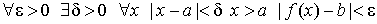
Обозначение 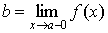

Если 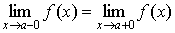
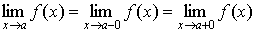
Теорема, устанавливающая связь понятий предела функции и предела последовательности.
Для того, чтобы существовал 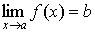
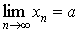
Свойства предельных значений.
Предельные значения имеют такие же свойства, что и предел последовательности:
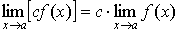
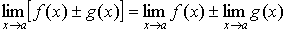
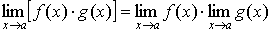
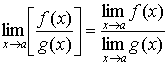
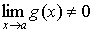
1.10 Предел монотонной функции
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1)> f ( x 2).
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1) f ( x 2).
Если f ( x ) при x a и ограничена сверху то существует конечный 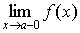
Если f ( x ) при x a но сверху не ограничена, то 
Аналогичные формулировки имеют место и для монотонно убывающей функции.
1.11 Признак Больцано-Коши существования предела функции.
Теорема. Для того, чтобы при x стремящимся к a существовал конечный 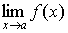
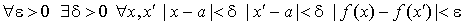
Эта теорема является одной из важнейших теорем теории пределов.
1.12 Сравнение бесконечно малых и бесконечно больших величин
1. Если существует 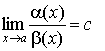
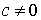
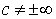
Обозначение: a = O ( b ) или b = O ( a ).
2. Если 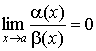
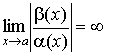
Обозначение a = o ( b ).
3. Если 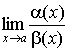
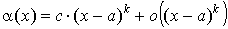
Слагаемое 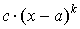
1. Если существует 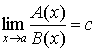
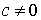
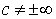
2. Если 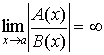
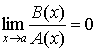
3. Если