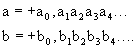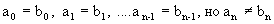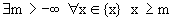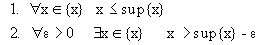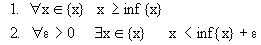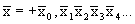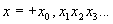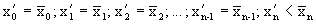Что такое sup в математике

Точные грани числовых множеств

Верхняя и нижняя грани числовых множеств.

Множество X вещественных чисел (X ⊂ \(\mathbb\)) называется ограниченным сверху, если существует вещественное число C такое, что все элементы множества X не превосходят C, то есть
$$
\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \leq \ C.\label
$$

Всякое вещественное число C, обладающее свойством \eqref, называется верхней гранью числового множества X.

Аналогично, множество X ⊂ \(\mathbb\) называется ограниченным снизу, если
$$
\exists C’\in\mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geq \ C’.\label
$$

Всякое вещественное число С ‘ , удовлетворяющее условию \eqref, называют нижней гранью числового множества X.

Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb\ \exists C\in\mathbb: \ \forall x\in X \ \rightarrow \ C’ \ \leq \ x \ \leq \ C\right\>\).

Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb\)>.

По условию \(B=\left\<\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geqslant \ C\right\>\). Поэтому
$$
\rceil B=\left\<\forall C \ \in \ \mathbb: \ \exists x_C \ \in \ X \ \rightarrow \ x_C Определение 1.

Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:

Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.

Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.

Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:

Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.

Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:

Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref. Пусть C=c₀,c₁c₂…c_n…; тогда c₀ — неотрицательное целое число, причем C x’.\label$$

Возьмем произвольное число x ∈ X и пусть x = a₀,<a_n>. Чтобы проверить выполнение условия \eqref, рассмотрим три произвольных случая:

$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$\exists m: \ x\in X_, \ x\not\in X_\label$$

Из \eqref следует, что \(a_0 удовлетворяет произвольный элемент \(\widetilde x\in X_m\), так как

Из неравенства \eqref следует, что sup X есть нижняя грань множества Y. Точная нижняя грань множества Y, то есть число inf Y, есть наибольшая из всех нижних граней множества Y. Значит, sup X ≤ inf Y.

Источник

Супремум и инфимум числовых множеств.

Дата добавления: 2015-08-14 ; просмотров: 19990 ; Нарушение авторских прав

Выше было описано правило, устанавливающее признак равенства двух вещественных чисел. Опишем теперь правило, позволяющее установить, какое из двух вещественных чисел больше.

Найдем первую по порядку цифру в этих числах, которые не равны друг другу. Пусть это будет цифра с номером n, т.е.

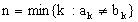
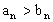
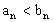
(заметим,что символами математики это записывается так: ). Тогда, если , то считаем, что a>b, а если , то a |b| то считаем, что а b.

Это правило будет необходимо нам ниже.

Определение. Множество, элементами которого являются вещественные числа, называется числовым множеством.

Числовые множества мы будем обозначать , где под х будут пониматься вещественные числа.

Для того, чтобы все дальнейшие определения и теоремы записывались в принятой математической форме, введем специальные значки, которые носят название кванторов. Их два:

Знак называется “квантор общности” и читается “для каждого” ( есть перевернутая буква А из английского выражения “for All”).

Знак называется “квантором существования” и читается “существует” ( есть перевернутая буква Е из английского слова “Exist”). Вариантом этого квантора является знак !, который читается “существует единственный” или “существует один и только один”.

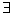
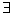
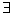
А теперь перейдем к определениям.

Определение 2. Числовое множество называется ограниченным снизу, если . Число m называется нижней гранью числового множества .

Определение 3. Числовое множество 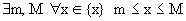называется ограниченным, если .

Очевидно,что если, скажем, существует одна верхняя грань, то их бесконечно много: если, например, М – верхняя грань числового множества ,то М+1, М+2, М+3 и т.д. – также верхние грани для .

Определение 4. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества (обозначение sup).

Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества (обозначение inf).

Эти понятия столь важны, что опишем их в других терминах.

Sup определяется двумя свойствами:

Первое свойство означает, что sup – верхняя грань, т.е. все элементы не превосходят sup.

Второе свойство означает, что любая попытка уменьшить эту верхнюю грань приводит к появлению элемента из 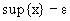, который окажется больше .

Говоря образно, sup это планка, перепрыгнуть которую нельзя, но любая попытка опустить эту планку хоть чуть-чуть приводит к тому, что кто-то ее преодолевает.

Аналогично, inf определяется двумя свойствами:

Заметим, что сами sup и inf могут как принадлежать, так и не принадлежать множеству x.

Теперь мы в состоянии доказать важнейшую теорему этого раздела и одну из важнейших теорем всего мат. анализа.

Теорема о существовании супремума и инфимума.

Если числовое множество не пусто и ограничено сверху, то у него существуетsup.

Если числовое множество не пусто и ограничено снизу, то у него существуетinf.

Мы докажем эту теорему только для sup при одном дополнительном предположении – в множестве имеются положительные числа. Доказательство разбивается на три части.

Пусть М – верхняя грань для 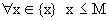, т.е. . Проделаем следующее построение:

а) Выбросим из множества все отрицательные числа.

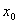
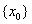
б) У оставшихся чисел выпишем те цифры , которые стоят перед запятой. Множество этих цифр конечно, т.к. этих цифр не более чем [M] (целая часть М). Обратите внимание, что именно в этом месте используется ограничение теоремы – существование верхней грани. Если бы верхней грани не существовало, то множество было бы бесконечным.

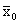
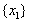
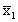
в) Выбросим из все те числа, у которых цифра до запятой меньше . У оставшихся чисел выпишем первую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .

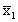
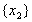
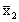
г) Выбросим из все те числа, у которых первая цифра после запятой меньше . У оставшихся чисел выпишем вторую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .

д) Выбросим из все те числа, у которых…

Повторяя эту операцию до бесконечности мы построим число

Покажем,что 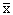и естьsup.

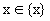
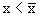
Возьмем любое . Если х имеет знак –, то ясно, что .

Пусть х имеет знак +. Тогда

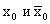
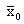
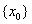
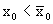
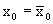
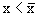
Сравним . Вспомним, что было самым большим из . Поэтому может быть всего два варианта: либо , либо . В первом случае и дальнейшая проверка ни к чему.

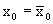
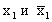
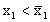
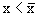
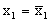
Если же , то сравним . Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .

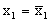
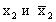
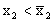
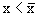
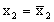
Если , то сравним . Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .

Продолжая этот процесс и дальше, получим, что возможны два следующих варианта.

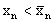
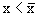
а) Найдется какое-то n, для которого . Тогда .

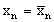
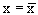
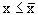
б) Для всех n . Тогда . Поэтому всегда и первое свойство супремума выполнено.

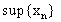
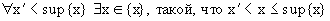
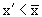
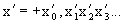
Заметим,что второе свойство можно записать так: . Возьмем положительное :

.

Так как 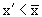, то найдется такое n,что

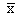
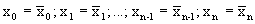
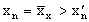
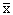
но вспомним процедуру построения . На n-м шаге после выбрасывания во множестве оставались лишь те числа, для которых . Любое из этих чисел будет больше x’ (т.к. ), но естественно, меньше или равно . Поэтому любое из этих чисел удовлетворяет второму свойству супремума.

Источник

множество к примеру

задан 1 Ноя ’15 16:27

1 ответ

Мы видим, что у этого множества есть min (наименьшее значение). Оно равно нулю. Если такая точка есть, что она же будет и inf (точной нижней гранью).

Теперь посмотрим на другую сторону. Мы видим, что наибольшее значение ни в какой точке не достигается, потому что за каждым числом имеется следующее, и оно больше предыдущего. Значит, max (наибольшее значение) у множества отсутствует. Но оно ограничено сверху: все рассматриваемые числа чего-то не превосходят. Например, верно то, что все они не больше 100. В таком случае число 100 разрешается называть верхней гранью множества. Ясно, что и многие другие числа обладают этим свойством: например, 50, или 2, или 3/2. Всё это верхние грани. Мы хотим выбрать из них «лучшую», то есть наиболее точную. Ясно, что это будет число 1. Все наши числа не превосходят 1, то есть это верхняя грань. При этом она самая маленькая из возможных: уменьшить её уже нельзя. Дело в том, что наши числа подходят к ней всё ближе и ближе. И если мы уменьшим 1 до, скажем, 0,999, то верхней грани уже не получится, так как число 1-1/n выйдет за указанные пределы, оказавшись правее 0,999 при n > 1000.

Точная верхняя грань (строгое определение см. в учебнике, а также условия, при которых она у множества существует), обозначается как sup. В рассмотренном примере max A отсутствует, но sup A = 1.

Если требуются ещё какие-то пояснения, их можно будет добавить.

Источник

Почему такие определения эквивалентны определениям лимсупа и лиминфа как супремума и инфимума пределов подпоследовательностей?

задан 26 Дек ’17 2:34

wart
219 ● 2 ● 8
71&#037 принятых

1 ответ

Достаточно разобрать случай верхнего предела. Он равен +бесконечности некоторая из подпоследовательностей стремится к +бесконечности. Тут всё просто. Это свойство также равносильно отсутствию ограниченности сверху.

Для ограниченных сверху последовательностей проверим эквивалентность обоих определений (старое звучало многократно; повторяться не будем).

Второй факт: что к a мы можем подойти сколь угодно близко. Задаём eps > 0 и номер m. Рассматриваем подпоследовательность, сходящуюся к a. Достаточно далёкие её члены находятся от a на расстоянии меньше eps, поэтому все они больше a-eps. Этих членов бесконечно много; среди них есть члены с номерами > m.

Обратная импликация: пусть a обладает свойствами из текста. Проверим, что у последовательности имеется подпоследовательность, стремящаяся к a, а также то, что никакому b > a частичный предел не равен. Начинаем со второго. Полагая eps=(b-a)/2, по условию делаем вывод, что правее a+eps=(a+b)/2 имеется только конечное число членов последовательности. Очевидно, что из них не образовать последовательность, стремящуюся к b.

По первому: строим последовательность натуральных чисел n1 a при k стремящемся к бесконечности. Для начала выбираем n1 так, что a(n1) > a-1. Далее n2 > n1 выбираем так, что a(n2) > a-1/2. Затем n3 > n2, где a(n3) > a-1/3, и так далее.

Источник

множество к примеру

задан 1 Ноя ’15 16:27

1 ответ

Мы видим, что у этого множества есть min (наименьшее значение). Оно равно нулю. Если такая точка есть, что она же будет и inf (точной нижней гранью).

Теперь посмотрим на другую сторону. Мы видим, что наибольшее значение ни в какой точке не достигается, потому что за каждым числом имеется следующее, и оно больше предыдущего. Значит, max (наибольшее значение) у множества отсутствует. Но оно ограничено сверху: все рассматриваемые числа чего-то не превосходят. Например, верно то, что все они не больше 100. В таком случае число 100 разрешается называть верхней гранью множества. Ясно, что и многие другие числа обладают этим свойством: например, 50, или 2, или 3/2. Всё это верхние грани. Мы хотим выбрать из них «лучшую», то есть наиболее точную. Ясно, что это будет число 1. Все наши числа не превосходят 1, то есть это верхняя грань. При этом она самая маленькая из возможных: уменьшить её уже нельзя. Дело в том, что наши числа подходят к ней всё ближе и ближе. И если мы уменьшим 1 до, скажем, 0,999, то верхней грани уже не получится, так как число 1-1/n выйдет за указанные пределы, оказавшись правее 0,999 при n > 1000.

Точная верхняя грань (строгое определение см. в учебнике, а также условия, при которых она у множества существует), обозначается как sup. В рассмотренном примере max A отсутствует, но sup A = 1.

Если требуются ещё какие-то пояснения, их можно будет добавить.

Источник