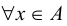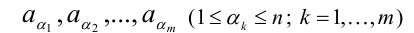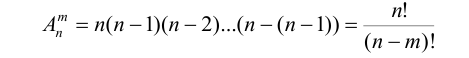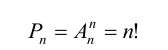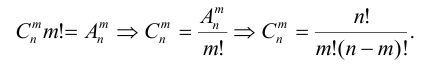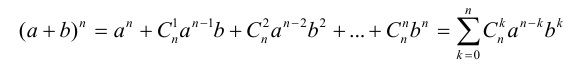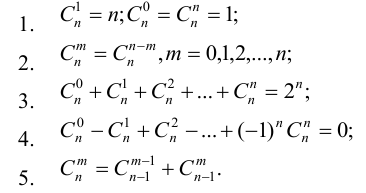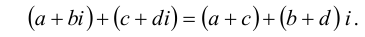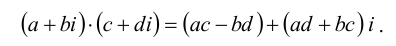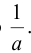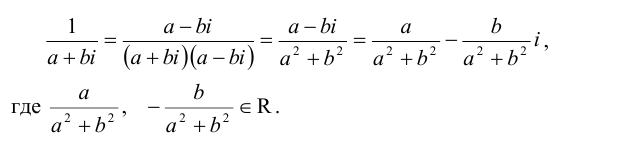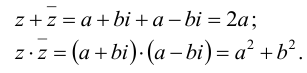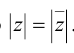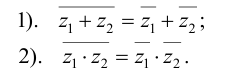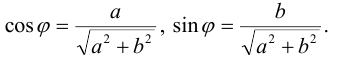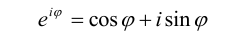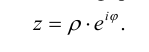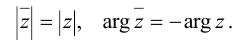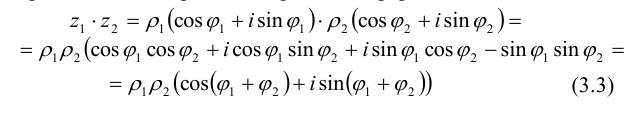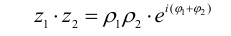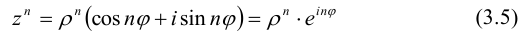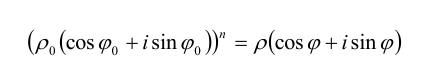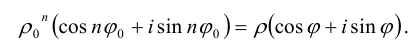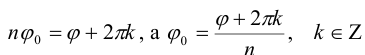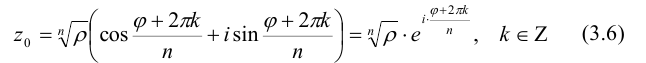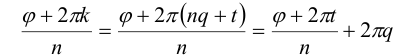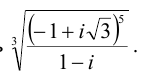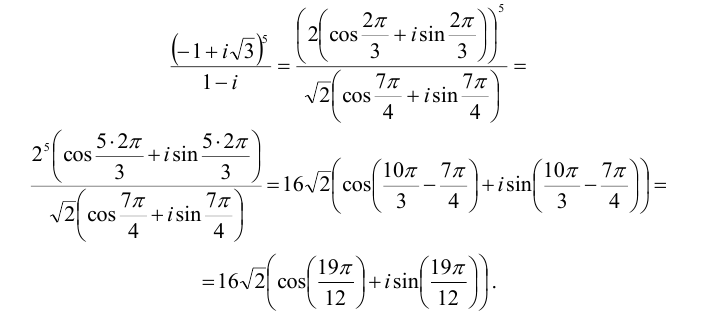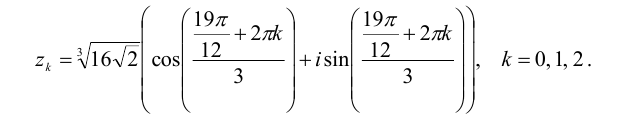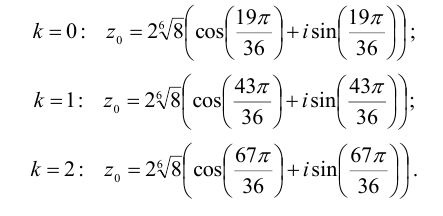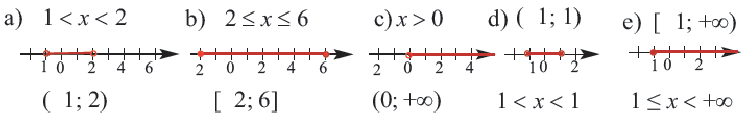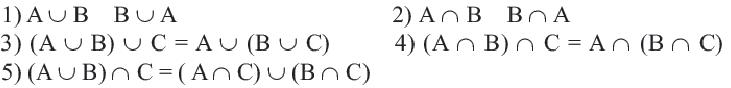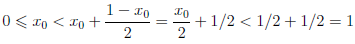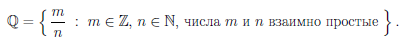Что такое sup inf

Точные грани числовых множеств

Верхняя и нижняя грани числовых множеств.

Множество X вещественных чисел (X ⊂ \(\mathbb\)) называется ограниченным сверху, если существует вещественное число C такое, что все элементы множества X не превосходят C, то есть
$$
\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \leq \ C.\label
$$

Всякое вещественное число C, обладающее свойством \eqref, называется верхней гранью числового множества X.

Аналогично, множество X ⊂ \(\mathbb\) называется ограниченным снизу, если
$$
\exists C’\in\mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geq \ C’.\label
$$

Всякое вещественное число С ‘ , удовлетворяющее условию \eqref, называют нижней гранью числового множества X.

Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb\ \exists C\in\mathbb: \ \forall x\in X \ \rightarrow \ C’ \ \leq \ x \ \leq \ C\right\>\).

Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb\)>.

По условию \(B=\left\<\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geqslant \ C\right\>\). Поэтому
$$
\rceil B=\left\<\forall C \ \in \ \mathbb: \ \exists x_C \ \in \ X \ \rightarrow \ x_C Определение 1.

Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:

Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.

Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.

Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:

Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.

Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:

Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref. Пусть C=c₀,c₁c₂…c_n…; тогда c₀ — неотрицательное целое число, причем C x’.\label$$

Возьмем произвольное число x ∈ X и пусть x = a₀,<a_n>. Чтобы проверить выполнение условия \eqref, рассмотрим три произвольных случая:

$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$\exists m: \ x\in X_, \ x\not\in X_\label$$

Из \eqref следует, что \(a_0 удовлетворяет произвольный элемент \(\widetilde x\in X_m\), так как

Из неравенства \eqref следует, что sup X есть нижняя грань множества Y. Точная нижняя грань множества Y, то есть число inf Y, есть наибольшая из всех нижних граней множества Y. Значит, sup X ≤ inf Y.

Источник

Содержание:

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление.

Наиболее распространенные числовые множества:

Основные понятия о числовых множествах

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

Некоторое непустое подмножество А множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число К такое, что

Всякое число К с указанным свойством называют верхней (нижней) гранью множества А.

Непустое подмножество А множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество А называется неограниченным сверху (снизу), если какое бы число К мы бы не предложили в качестве верхней (нижней) границы множества А, всегда найдется элемент этого множества, который будет больше (меньше) К.

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел А называют точной верхней гранью этого множества и обозначают sup А. Наибольшую из нижних граней непустого подмножества множества действительных чисел А называют точной нижней гранью этого множества и обозначают inf А. Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Соединения. Бином Ньютона

Рассмотрим совокупность n различных элементов. Произвольная упорядоченная выборка из этих элементов: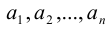

называется соединением. Эта выборка может быть как без повторений, так и с повторениями.

Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.

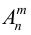
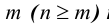
Размещениями из п элементов поназывают их соединения, каждое из которых содержит ровно m различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.

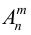
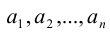
Определим число размещений из n элементов по m.

Соединения из n элементов, каждое из которых содержит все n элементов, и которые отличаются лишь порядком элементов, называются перестановками .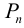

Перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

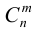
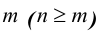
Сочетаниями из n элементов по называют такие их соединения, каждое из которых содержит ровно m данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .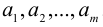

Делая в каждом из них m! возможных перестановок их элементов, очевидно, получим все размещения из n элементов по m:

Числа 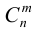являются коэффициентами в формуле бинома Ньютона:

Это свойство позволяет последовательно вычислять биномиальные коэффициенты С»‘ с помощью так называемого треугольника Паскаля:

Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.

Комплексные числа

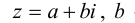
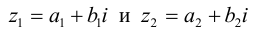
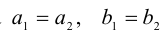
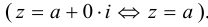
Действительное число а называется действительной частью комплексного числа — мнимой частью или коэффициентом при мнимой единице. Два комплексных числа будут равны тогда и только тогда, когда При этом действительные числа рассматриваются как частный случай комплексных чисел, мнимая часть которых равна нулю . Комплексное число равно нулю тогда и только тогда, когда равны нулю его действительная и мнимая части.

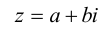
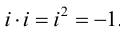
Операции сложения, вычитания и умножения над числами вида производятся по обычным правилам алгебры с единственным дополнительным условием: .

Операции над комплексными числами

Алгебраическую операцию сложения на множестве С можно задать следующим образом:

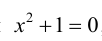
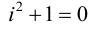
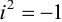
Учитывая, что через i обозначен корень уравнения т.е. или , можно определить умножение комплексных чисел:

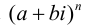
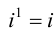
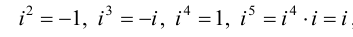
Умножение также ассоциативно и коммутативно. Произведение нескольких сомножителей вычисляется как последовательное умножение. Натуральная степень комплексного числа может быть найдена при помощи формулы бинома Ньютона. Поскольку , , при возведении i в любую натуральную степень n, надо найти остаток от деления n на 4 и возвести i в степень, равную этому остатку.

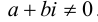
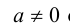
Чтобы определить деление комплексных чисел, нужно определить число обратное числу . Для действительного числа обратным будет число

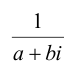
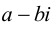
Выражение запишем в стандартной форме. Для этого умножим числитель и знаменатель на комплексное число :

Значит, для любого ненулевого комплексного числа существует обратное. Таким образом, операция деления определена как произведение делимого на число, обратное делителю.

Множество комплексных чисел является расширением множества действительных чисел, любое действительное число а можно записать в виде .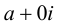

Число а-b называется сопряженным числу z = a + bi и обозначается .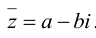

Сумма и произведение сопряженных чисел являются числами действительными:

Число 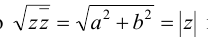называется модулем или абсолютной величиной комплексного числа a + bi. Очевидно, что

Свойства сопряжения:

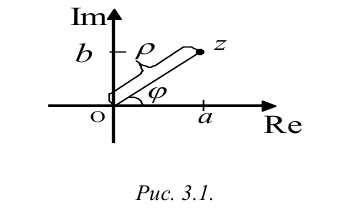
Каждому комплексному числу z = a + bi поставим в соответствие точку Z плоскости, координатами которой в прямоугольной системе координат являются числа а и b.

Тогда каждой точке Z(a,b) плоскости будет соответствовать единственное комплексное число a + bi. В результате получается взаимно однозначное соответствие между множеством комплексных чисел С и множеством точек плоскости, которое позволяет отождествить произвольное комплексное число a + bi с точкой плоскости, имеющей в выбранной системе координат координаты (a,b). При этом точки горизонтальной координатной оси Re изображают действительные числа и поэтому эту ось называют действительной осью, а по вертикальной оси Im откладываются мнимые части комплексных чисел, поэтому вертикальная ось Im называется мнимой осью.

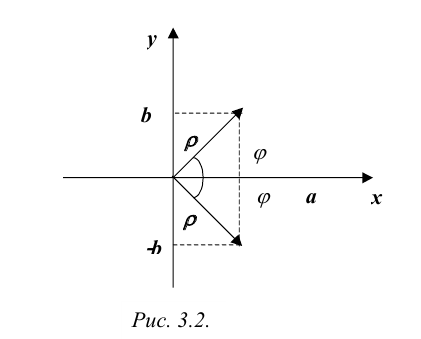
Расстояние от точки Z до начала координат есть действительное неотрицательное число р, которое называется модулем комплексного числа z = a + bi и обозначается \z\ = p. Угол между положительным направлением действительной оси и радиус-вектором точки z называется аргументом z и обозначается arg z. Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных 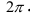, при этом положительные углы отсчитываются против часовой стрелки.

Пусть z = a + bi. Из рис. 3.1 ясно, что модуль числа z находится

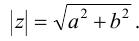
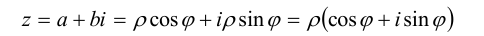
по формуле Аргумент числа z определяется из равенств

(3.1)

Запись числа z в виде (3.1) называется тригонометрической формой комплексного числа.

Если воспользоваться формулой Эйлера,

то от тригонометрической формы записи комплексного числа (3.2) несложно перейти к его показательной форме записи:

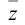
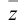
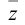
Пусть z и — сопряженные числа. Если z = а + bi, то = a- bi. Геометрически z и являются точками, симметричными относительно действительной оси (рис. 3.2). Отсюда вытекают равенства

Перемножать и делить комплексные числа удобнее, если они представлены в тригонометрической форме:

В показательной форме:

При умножении комплексных чисел их аргументы складываются, а модули перемножаются. Это правило верно для любого числа сомножителей. Аналогично,

(3 4)

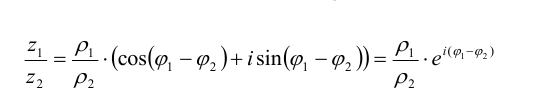
При вsполнении деления комплексных чисел в тригонометрической форме их аргументы вычитаются, а модули нужно разделить.

Формула Муавра. Извлечение корня из комплексного числа

Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра:

Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.

Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, 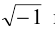не существует. В множестве комплексных чисел дело обстоит иначе.

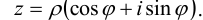
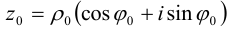
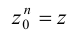
Пусть . Комплексное число

называется корнем n-й степени из z, если

, т.е.:

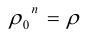
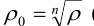
Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).

Аргумент комплексного числа определяется с точностью до

. Следовательно,

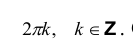
Придавая А- различные значения, мы не всегда будем получать различные корни. Действительно, k можно записать в виде k = nq + t, где 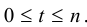. Тогда:

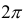
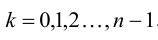
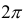
Т.е. значение аргумента при данном к отличается от значения аргумента при k = t на число, кратное . Следовательно, в формуле (2) можно ограничится лишь значениями . При таких значениях к получаются различные корни, так как разность между их аргументами по абсолютной величине меньше .

Пример:

Вычислить

Решение:

Представим число, стоящее под знаком корня, в тригонометрической форме:

Извлечем далее корень третьей степени из этого комплексного числа:

Отсюда полагая, что k = 0,1,2, получим:

Числовые множества и форма их представления

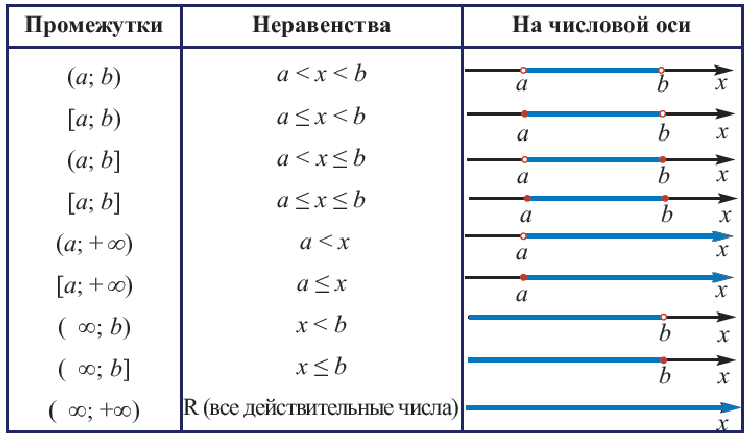
Множество, элементы которого являются действительными числами называется числовым множеством. В основном, числовые множества задаются в виде неравенств или в виде промежутков. Множество всех действительных чисел обозначается как

Пример:

Изобразите на координатой прямой множество чисел, удовлетворяющих неравенству. Запишите в виде промежутков.

Свойства объединения и пересечения числовых множеств

Некоторые свойства пересечения и объединения множеств подобны переместительным, сочетательным и распределительным свойствам сложения и умножения чисел.

Верные для множеств равенства, соответствующие свойствам 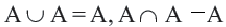для чисел не всегда верны.

Пример:

Графиком функции 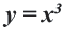называется кубическая парабола.

Поэтому график функции проходит через начало координат и расположен в I и III четвертях. Если значение заменить его противоположным значением , тогда функция будет принимать противоположное значение: т.к. , то . Значит, каждой точке графика функции соответствует точка , симметричная относительно начала координат на данном графике. Таким образом, график функции симметричен относительно начало координат. По графику видно, что число , куб которого равен данному числу — единственное.

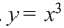
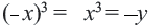
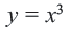
Свойства числовых множеств

Ограниченные числовые множества

С помощью логических символов ограниченность сверху множества X записывают следующим образом:

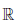
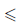
∃ a ∈ : x a, ∀x ∈ X.

Учитывая свойства модуля числа, можно дать следующее равносильное определение граниченного множества.

Определение 1.27. Непустое числовое множество X называют ограниченным, если существует такое положительное число M, что

|x| M, ∀x ∈ X.

Определение 1.28. Элемент a из числового множества X называют максимальным (минимальным) элементом в X, если x a (соответственно, x > a) для любого x из X, и пишут: a = max X (соответственно, a = min X).

В силу аксиомы порядка (3.b) легко показать, что если множество X в 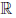имеет максимальный (минимальный) элемент, то он единственен.

Отметим, что если числовое множество X имеет максимальный (минимальный) элемент a, то оно ограничено сверху (снизу) и число a является верхней (нижней) границей множества X. Однако не всякое ограниченное сверху (снизу) числовое множество имеет максимальный (минимальный) элемент.

Замечание. Любое числовое множество, содержащее конечное число элементов, имеет максимальный и минимальный элементы.

Теорема 1.2 (принцип полноты Вейерштрасса). Если непустое числовое множество ограничено сверху (снизу), то существует число, которое является наименьшей верхней (соответственно, наибольшей нижней) границей этого множества, и это число единственно.

∃ c ∈ 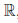: x c y, ∀x ∈ X, ∀y ∈ Y.

Определение 1.29. Пусть X — непустое ограниченное сверху числовое множество. Наименьшую из верхних границ множества X называют точной верхней границей или верхней гранью множества X и обозначают sup X (читают «супремум X») или sup x.

Итак, sup X = min| x c, ∀x ∈ X> и потому определение 1.29 равносильно следующему.

1. x a, ∀x ∈ X ;

С учетом определения 1.29 принцип полноты множества R в смысле Вейер-штрасса формулируется следующим образом:

Теорема 1.3. Непустое ограниченное сверху числовое множество имеет, притом единственную, точную верхнюю границу.

Аналогично вводится понятие точной нижней границы множества.

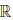
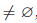
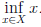
Определение 1.31. Пусть X ⊂ , X , ограничено снизу. Наибольшую из его нижних границ называют точной нижней границей или нижней гранью множества X и обозначают inf X (читают «инфимум X») или .

Характеристическими свойствами a = inf X, a ∈ 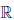, являются:

1) a x, ∀x ∈ X ; 2) ∀ε > 0 ∃ xε ∈ X : xε a + ε.

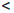
Лемма 1.2. Если числовое множество X имеет максимальный (минимальный) элемент a, то a = sup X (соответственно a = inf X).

Следовательно, по определению 1.30 a = sup X.

Пример 1.6. Найти sup X, если X = [0, 1).

Неограниченные числовые множества

Определение 1.32. Если непустое числовое множество не является ограниченным сверху (снизу), то его называют неограниченным сверху (снизу).В символьной форме это определение принимает вид:

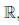
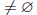
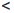
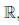
X ⊂ , X не ограничено сверху ⇒ ∀a ∈ ∃ x ∈ X : x>a.

В случае, если числовое множество X не ограничено сверху считают, что его точная верхняя граница равна +∞.

Из сказанного и теоремы 1.2 вытекает следующий результат.

Теорема 1.5. Непустое ограниченное сверху (снизу) подмножество множества Z имеет максимальный (минимальный) элемент.

Теорема 1.6. Бесконечное подмножество натуральных чисел не ограничено сверху.

Теорема 1.7 (принцип Архимеда). Для любого числа a и любого положительного числа b найдется единственное целое число n₀ такое, что (n₀-1)b a n₀b.

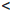
Следствие 1. Для любого числа x ∈ существует единственное число k ∈ такое, что (достаточно в теореме положить b = 1). Такое число k называют целой частью числа x и обозначают через [x] или E (x).

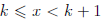
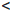
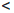
Следствие 2. Для любого положительного числа ε существует натуральное число n такое, что 0 1/n ε.

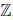
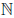
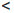
Пусть ε — положительное число. По принципу Архимеда найдется такое n ∈ , что n > 1∕ε. Поскольку ε > 0, то n ∈ и 0 1/n ε.

Теорема 1.8 (о плотности в ). Для любых чисел a, b ∈ , a b, найдется рациональное число r такое, что a r b.

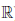
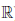
Число b — a положительно. По следствию 2 принципа Архимеда подберем натуральное число n₀ такое, что 0 1∕n₀ b—a. Далее, по принципу Архимеда по числу a и 1∕n₀ > 0 найдется m0 ∈ :

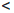
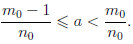
Докажем, что рациональное число m₀∕n₀ — искомое. Действительно,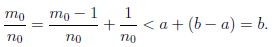

Отсюда, a m_o∕n_o b.

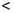
Счетные и несчетные множества

При изучении множеств приходится по некоторым правилам сравнивать их между собой по запасу элементов. Изложим одно такое правило.

Пусть n — натуральное число, а N_n = : k n>. Множество X называют конечным, если существует такое n ∈ , что между множествами X и N_n можно установить биективное отображение, в противном случае множество X называют бесконечным.

Пример 1.7. Множество X натуральных четных чисел счетно, поскольку функция f : 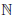→ X, f(n) = 2n, является биекцией.

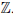
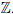
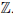
Пример 1.8. Множество целых чисел счетно. В этом случае биективное отображение f : N → , f(n) = (-1)n-1 [n/2], позволяет пронумеровать элементы множества следующим образом:

Теорема 1.9. Любое бесконечное множество содержит счетное подмножество.

В результате получим множество Y = 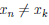>, которое является счетным, так как при

Теорема 1.10. Объединение конечной или счетной совокупности счетных множеств есть счетное множество.

Пронумеруем элементы множества A следующим образом:

Следствие. Множество рациональных чисел счетно.

Множество рациональных чисел определяется следующим образом:

Расположим рациональные числа в таблицу. Сначала в первую строку поместим все целые числа в порядке не убывания их абсолютных величин и так, что за каждым натуральным числом следует ему противоположное:

Во вторую строку поместим все несократимые рациональные числа со знаменателем 2 в порядке не убывания их абсолютных величин, причем вслед за каждым положительным числом следует ему противоположное:

Аналогично, в n-ую строку выпишем все несократимые рациональные числа со знаменателем n, упорядоченные по абсолютной величине и вслед за каждым положительным числом вписано ему противоположное. В результате получим таблицу всех рациональных чисел, состоящую из счетного множества строк, каждая из которых содержит счетное множество элементов. При этом среди выписанных элементов нет одинаковых. По теореме 8 множество 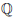счетно.

Определение 1.34. Конечные и счетные множества называют не более чем счетными.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник