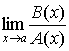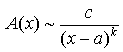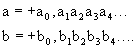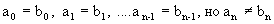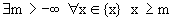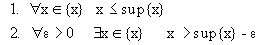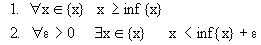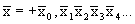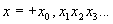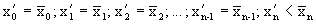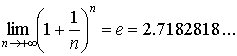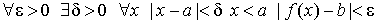Что такое sup и inf множества
Точные грани числовых множеств
Верхняя и нижняя грани числовых множеств.
Множество X вещественных чисел (X ⊂ \(\mathbb
$$
\exists C \ \in \ \mathbb
$$
Всякое вещественное число C, обладающее свойством \eqref
Аналогично, множество X ⊂ \(\mathbb
$$
\exists C’\in\mathbb
$$
Всякое вещественное число С ‘ , удовлетворяющее условию \eqref
Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb
Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb
По условию \(B=\left\<\exists C \ \in \ \mathbb
$$
\rceil B=\left\<\forall C \ \in \ \mathbb
Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:
Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.
Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.
Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:
Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.
Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:
Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref
Возьмем произвольное число x ∈ X и пусть x = a0,<an>. Чтобы проверить выполнение условия \eqref
$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label
$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label
$$\exists m: \ x\in X_
Из \eqref
Из неравенства \eqref
Супремум и инфимум числовых множеств.
Дата добавления: 2015-08-14 ; просмотров: 19991 ; Нарушение авторских прав
Выше было описано правило, устанавливающее признак равенства двух вещественных чисел. Опишем теперь правило, позволяющее установить, какое из двух вещественных чисел больше.
Найдем первую по порядку цифру в этих числах, которые не равны друг другу. Пусть это будет цифра с номером n, т.е.
(заметим,что символами математики это записывается так: 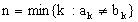
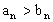
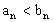
Это правило будет необходимо нам ниже.
Определение. Множество, элементами которого являются вещественные числа, называется числовым множеством.
Числовые множества мы будем обозначать
Для того, чтобы все дальнейшие определения и теоремы записывались в принятой математической форме, введем специальные значки, которые носят название кванторов. Их два:
Знак 

Знак 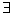
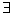
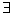
А теперь перейдем к определениям.
Определение 2. Числовое множество
Определение 3. Числовое множество 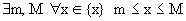
Очевидно,что если, скажем, существует одна верхняя грань, то их бесконечно много: если, например, М – верхняя грань числового множества
Определение 4. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества
Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества
Эти понятия столь важны, что опишем их в других терминах.
Sup
Первое свойство означает, что sup
Второе свойство означает, что любая попытка уменьшить эту верхнюю грань приводит к появлению элемента из 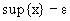
Говоря образно, sup
Аналогично, inf
Заметим, что сами sup
Теперь мы в состоянии доказать важнейшую теорему этого раздела и одну из важнейших теорем всего мат. анализа.
Теорема о существовании супремума и инфимума.
Если числовое множество
Если числовое множество
Мы докажем эту теорему только для sup
Пусть М – верхняя грань для 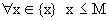
а) Выбросим из множества
б) У оставшихся чисел выпишем те цифры 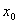
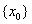
в) Выбросим из 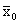
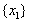
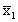
г) Выбросим из 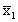
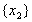
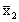
д) Выбросим из
Повторяя эту операцию до бесконечности мы построим число
Покажем,что 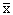
Возьмем любое 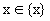
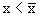
Пусть х имеет знак +. Тогда
Сравним 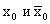
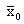
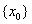
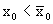
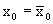
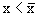
Если же 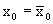
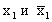
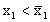
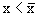
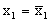
Если 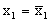
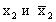
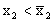
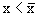
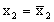
Продолжая этот процесс и дальше, получим, что возможны два следующих варианта.
а) Найдется какое-то n, для которого 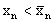
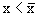
б) Для всех n 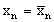
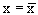
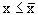
Заметим,что второе свойство 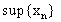
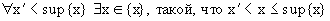
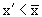
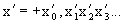
Так как 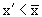
но вспомним процедуру построения 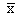
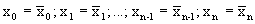
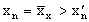
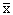
1. Теория пределов
1.1 Супремум и инфимум
Определение 1. Множество < x >, элементами которого являются числа, называется числовым множеством.
Определение 2. Множество вещественных чисел < x > называется ограниченным сверху (снизу), если существует число M ( m ) такое, что 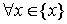
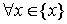
Число M называется верхней гранью числового множества < x >. Аналогично, число m называется нижней гранью числового множества < x >.
Верхних (нижних) граней бесконечно много, так как любое число, большее M (меньшее m ), есть также верхняя (нижняя) грань.
Определение 3. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества < x > (обозначение sup < x >).
Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества < x > (обозначение inf < x >).
Более точно, эти понятия выражаются следующими свойствами:
1. 
2. 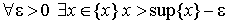
1. 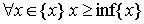
2. 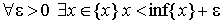
Теорема о существовании супремума и инфимума числового множества.
Если числовое множество < x > не пусто и ограничено сверху, то у него существует sup < x >.
Если числовое множество < x > не пусто и ограничено снизу, то у него существует inf < x >.
1.2 Последовательности
Определение 1. Числовой последовательностью (в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел
Обратите внимание на два момента.
1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!
2. Все числа упорядочены, то есть расположены в определенном порядке.
В дальнейшем для последовательности часто будем использовать сокращенное обозначение < xn >.
Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них.
1. Умножение последовательности на число.
Последовательность c × < xn > – это последовательность с элементами < c × xn >, то есть
2. Сложение и вычитание последовательностей.
или, более подробно,
3. Умножение последовательностей.
4. Деление последовательностей.
Естественно, предполагается, что в этом случае все yn ¹ 0.
Последовательность < xn > называется ограниченной сверху, если 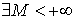
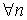
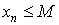
Последовательность < xn > называется ограниченной снизу, если 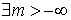
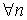
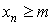
Последовательность < xn > называется ограниченной, если она одновременно ограничена и сверху и снизу.
1.3 Предел последовательности.
Основное определение. Число a называется пределом последовательности < xn > при n стремящимся к бесконечности, если
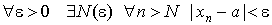
Для этого факта используют следующие обозначения:
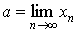
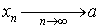
Говорят, что 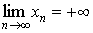
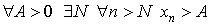
Говорят, что 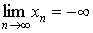
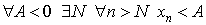
Последовательность < xn > называется бесконечно большой, если 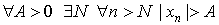
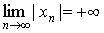
1.4 Бесконечно малые последовательности.
Оределение. Последовательность < xn > называется бесконечно малой, если 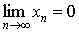

Бесконечно малые последовательности имеют следующие свойства.
1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.
2. Бесконечно малая последовательность ограничена.
3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
1.5 Сходящиеся последовательности.
Определение. Если существует конечный предел 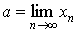
Сходящиеся последовательности имеют следующие свойства.
1. Сходящаяся последовательность ограничена.
2. 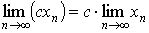
3. 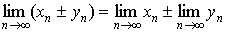
4. 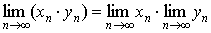
5. Если 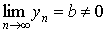
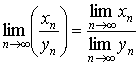
1.6 Предельный переход в неравенствах.
1. 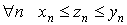
2. 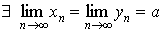
то существует 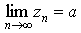
1.7 Предел монотонной последовательности.
Последовательность < xn > называется монотонно возрастающей, если для любого n xn +1 ³ xn .
Последовательность < xn > называется строго монотонно возрастающей, если для любого n xn +1 > xn .
Последовательность < xn > называется монотонно убывающей, если для любого n xn +1 £ xn .
Последовательность < xn > называется строго монотонно убывающей, если для любого n xn +1 xn .
Теорема о существовании предела монотонной последовательности.
1. Если последовательность < xn > монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup < xn > ( inf < xn > ).
На основании этой теоремы доказывается, что существует так называемый замечательный предел
1.8 Подпоследовательности
и рассмотрим последовательность 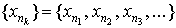
Если < xn > – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.
Лемма Больцано- Вейерштрасса.
1. Из любой ограниченной последовательности можно извлечь такую подпоследовательность, которая сходится к конечному пределу.
2. Из любой неограниченной последовательности можно извлечь бесконечно большую подпоследовательность.
На основании этой леммы доказывается один из основных результатов теории пределов –
Признак сходимости Больцано-Коши.
Для того, чтобы у последовательности < xn > существовал конечный предел, необходимо и достаточно, чтобы
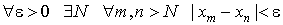
Последовательность, удовлетворяющая этому свойству, называется фундаментальной последовательностью, или последовательностью, сходящейся в себе.
1.9 Предел функции
Основное определение. Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к a (обозначение 
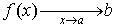
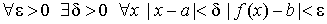
Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к + ¥ (обозначение 

Говорят, что функция f ( x ) стремится к + ¥ при x стремящимся к a (обозначение 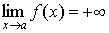
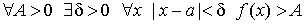
( 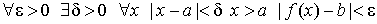
Обозначение 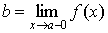

Если 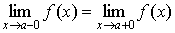
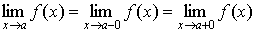
Теорема, устанавливающая связь понятий предела функции и предела последовательности.
Для того, чтобы существовал 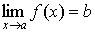
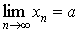
Свойства предельных значений.
Предельные значения имеют такие же свойства, что и предел последовательности:
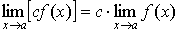
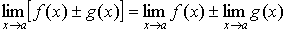
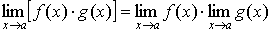
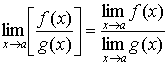
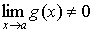
1.10 Предел монотонной функции
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1)> f ( x 2).
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1) f ( x 2).
Если f ( x ) при x a и ограничена сверху то существует конечный 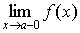
Если f ( x ) при x a но сверху не ограничена, то 
Аналогичные формулировки имеют место и для монотонно убывающей функции.
1.11 Признак Больцано-Коши существования предела функции.
Теорема. Для того, чтобы при x стремящимся к a существовал конечный 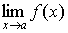
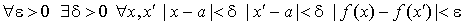
Эта теорема является одной из важнейших теорем теории пределов.
1.12 Сравнение бесконечно малых и бесконечно больших величин
1. Если существует 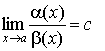
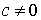
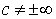
Обозначение: a = O ( b ) или b = O ( a ).
2. Если 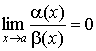
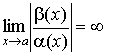
Обозначение a = o ( b ).
3. Если 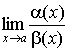
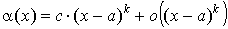
Слагаемое 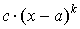
1. Если существует 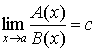
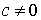
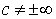
2. Если 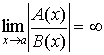
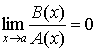
3. Если