Что такое np полная задача
User Tools
Site Tools
Sidebar
Table of Contents
NP класс и NP-полные задачи
$P$ – класс задач, решаемых за полиномиальное (от размера входа) время. Примеры таких задач: задача о существовании пути в графе, задача о взаимно простых числах и т.д.
Что такое полиномиальное время?
$NP$ – класс задач, верифицируемых (проверяемых) за полиномиальное время. Альтернативное определение: класс задач, решаемых за полиномиальное время на недетерминированной машине Тьюринга. Примеры таких задач: задача о выполнимости булевой формулы, задача о вершинном покрытии, задача о клике и т.д.
Существует два варианта:
Сертификат – дополнительная информация, позволяющая быстро решить задачу. Важно помнить, что размер сертификата должен быть полиномиален относительно размера самой задачи.
Алгоритм верификации – принимает на вход экземпляр задачи и сертификат к нему, а возвращает ответ к задаче, 0 или 1.
Что значит, что одна задача водима к другой за полиноминальное время?
Это значит, что существует полиномиальная функция, которая отображает экземпляр первой задачи в экземпляр второй задачи. Если входная задача соответствует положительному решению, то и выходная задача соответствует положительному решению. Если входная задача соответствует отрицательному решению, то и решение выходной задачи отрицательно.
Примеры: 3Sat, задача о вершинном покрытии (множество вершин, такое, что, у каждого ребра графа хотя бы один из концов входит в вершину из него) и т.д.
Существует два варианта:
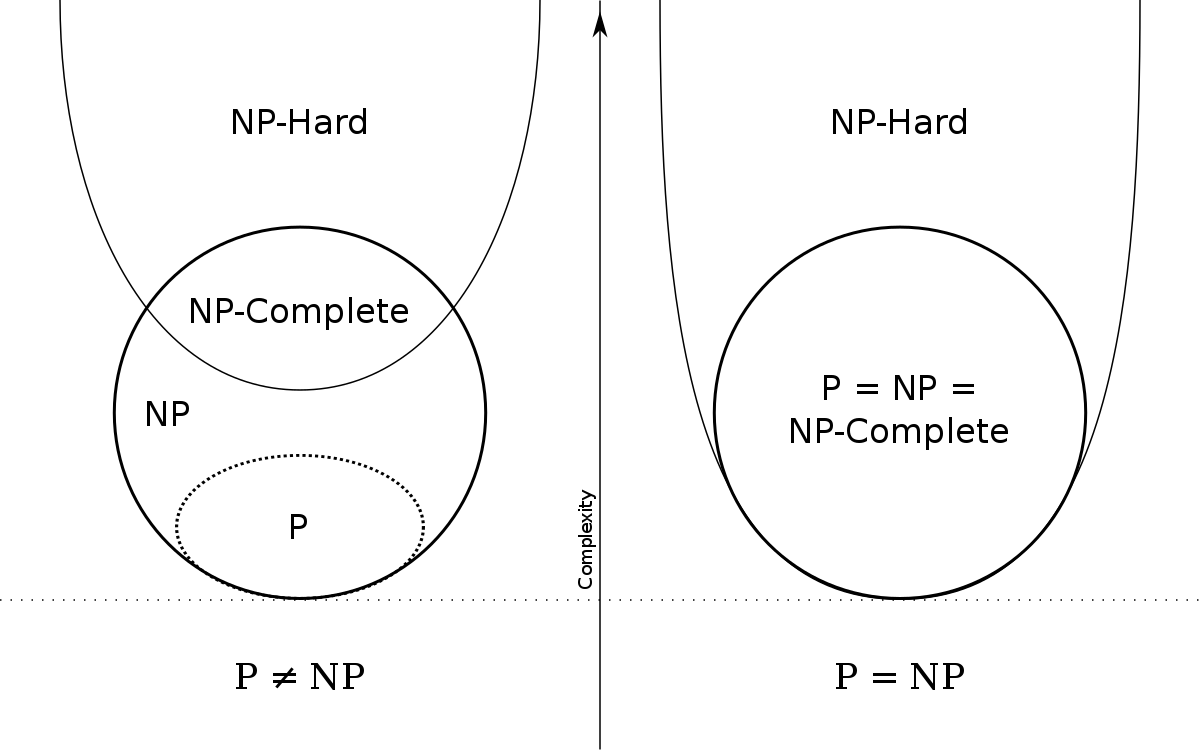
Общая схема классов
NP-полные задачи
Программист Вася регулярно встречается на работе с новыми для себя задачами. Он как обычно придумал решение, но в этот раз случилось так, что его алгоритм выполняется слишком долго. Временем нужно дорожить, поэтому Васе досталось от начальства. Эта проблема возникла сразу по двум причинам. Во-первых, наверняка задачу Васи уже кто-то решал, либо она сводится к уже решенной. Во-вторых, он не подумал о сложности выполнения алгоритма. Небольшой анализ предотвратил бы бесполезную трату времени.
Далеко не все задачи можно решить за разумное время. Возможно, наш герой столкнулся именно с такой. Сегодня мы познакомимся с группой задач, которые могут выполняться всю вашу жизнь даже при не очень больших размерах входных данных. Мы разберемся с понятием NP-полноты и временной сложности алгоритмов. И напоследок мы научимся доказывать то, что задача является NP-полной, сузив ее до более простой, но столь же долго решаемой. Зная это, Вася мог бы не тратить время, а объяснить начальству, что от него хотят невозможного.
Машины Тьюринга
Начнем с понятия, на котором строится теория сложности. Машина Тьюринга (МТ). Это всего лишь один из способов описания алгоритмов. Алгоритмы можно описывать на языках высокого уровня, математическими формулами и даже на словах, активно размахивая при этом руками. Тем не менее, машина Тьюринга обладает двумя ключевыми свойствами: она формальна и близка к реальным вычислительным устройствам (читай — компьютерам).
Благодаря формальности машины Тьюринга, можно математически доказывать утверждения об алгоритмах. Например, вывести, что количество операций в сортировке пузырьком квадратично зависит от длины массива. Чуть позже мы встретимся с более неочевидными утверждениями. Так как машина Тьюринга “похожа” на схему работы обычного компьютера, мы можем пользоваться этими утверждениями в работе.
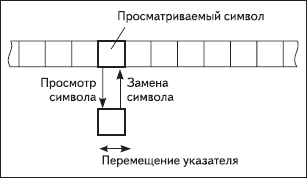
Я уже достаточно сказал о важности машины Тьюринга, но ничего о том, что она из себя представляет. Формально МТ определяется через три объекта: множество символов, множество состояний и правила перехода из одного состояния в другое. Технически же — это бесконечная лента, разделенная на ячейки. По этой ленте движется головка. За каждый шаг машины Тьюринга она может заменить содержимое обозреваемой ячейки, сдвинуться на одну ячейку и изменить состояние машины. Она заканчивает выполнение, когда приходит в конечное состояние (опредлеленное заранее). Результатом выполнения будет слово на ленте.
Классы сложности
Теперь мы готовы понять, как можно оценивать длительность выполнения алгоритмов. Временной сложностью алгоритма называется функция, которая зависит от длины исходных данных и характеризует число шагов работы алгоритма над этими данными. Мы не зря определили машину Тьюринга, так как оценивать сложность будем именно на ней. Таким образом, длина исходных данных — это число занятых ячеек перед началом выполнения МТ, а шаги работы соответствуют переходам при выполнении МТ.
Заметки Датасатаниста: что делать, если перед вами оказалась NP-полная задача
Наверное, каждый сталкивался с тем, что приходилось столкнуться с какой-то сложной задачей, решение к которой не удавалось подобрать не то что сразу — а даже после долгих упорных часов работы или дней. Об одном из классов таких задач — NP-полных, мы сегодня и поговорим.
А вообще реально ли встретить такие задачи в обычной жизни? На самом деле, они возникают в огромном ряде случаев: комбинаторика, графы и сети, выполнение логических формул, работа с картами, оптимальные загрузки, отображения, задачи дискретной оптимизации, нахождение самых длинных последовательностей, поиск равных сумм и многие задачи на множества! И это далеко не полный список.
Под катом неформальный гайд — как понять, что перед вам может быть NP задача и что делать, если это именно она и оказалась. Сегодня мы атакуем этот вопрос с практической стороны.
Убедиться, что перед вам действительно она
Как понять, что перед вами оказалась NP-полная задача? Во-первых, самая простая эвристика на обнаружение — поиск по уже известным NP-полным задачам с целью определить что-то похожее, таких списков немало — например.
Второе, рассмотреть следующие свойства задач:
Пример работы по данному списку
Приведем простой пример на задаче, которую недавно утвердили как NP-полную!
По материалам статьи. Нужно расставить N ферзей на доске размера N на N, при условии, что уже K Сведение
Почему имея на руках аналогичные задачи бывает непросто понять формально, что перед нами NP-задача? По-настоящему мы должны свети NP задачу к нашей, тогда мы точно будет знать, что наша задача NP-трудная! И если мы смогли ее смоделировать, как в списке выше, то она полная — то есть по крайней мере NP и не более чем NP, фактически “самая трудная среди NP задач” (как и остальные NP-полные).
Окей, надо ли оно нам? Не совсем, если вы прям уверены, после всех проверок, что перед вами NP-задача, то вам не нужно ничего доказывать, если вы не пишите научную статью.
А нужно либо (об этом всем мы поговорим ниже):
Не опускать руки!
Самое важное — это оценить размеры-параметры и реалистичные сценарии!
Например, вы знаете, что несмотря на то, что значения параметров не фиксированы, но условный N Распределение входных данных
Или несмотря на то, что в общем случае входные данные могут быть любыми, но опять же на примере ферзей — обычно фиксирован один ферзь или даже ни одного. Значит, что в 90% случаев вы можете использовать очень простое решение и вызывать сложное только в крайних случаях.
Пример, когда в среднем все обычные комбинации простые: задача о дополнении ферзей — мы знаем, что условный DFS + эвристики могут в большинстве случаев находить решения очень быстро, и только в очень нестандартных ситуациях быть крайней сложными.
Вот пример, того как оценивалось решение для очень специализированной задачи NP-полной tiling против общего метода моделирования целого класса таких задач с помощью методов логического программирования:
(из статьи Relational Data Factorization (Paramonov, Sergey; van Leeuwen, Matthijs; De Raedt, Luc: Relational data factorization, Machine Learning, volume 106))
Во-первых, скорость у спец решения LTM-k и общего метода существенно отличаются. Таким образом решение для именно такого типа задач на эвристиках может полностью решать эту проблему.
Во-вторых, пожертвовав качеством решения, общий приближенный метод давал очень похожую скорость.
Эвристики и аппроксимация
Последний и самый мощный инструмент — это использовать системы моделирования NP-полных задач, такие как например Answer Set Programming.
Подробнее про языки логического программирования.
Например решение задачи о расстановке ферзей будет выглядеть вот так:
Проведя простой эксперимент по поиску решений для разного количества ферзей N — мы получим следующее: по оси Х — ферзи, по Y — время в секунда по поиску решения:
Мы видим, что несмотря на то, что рост времени явно не полиномиальный (что и логично) мы хорошо справляемся с адекватным количеством ферзей и размерами доски.
Тогда, если мы знаем, какие размеры доски являются для нас реальным, мы можем понять насколько это точное решение приемлемо для нас в настоящей системе.
Выводы
Тезисно пройдемся, по идеям из статьи в виде чек листа
Еще немного про P и NP
Существует большая разница между задачами непростыми и задачами сложными. Задача может не иметь эффективных решений в самых худших случаях, но может оставаться легко решаемой для большинства случаев, или для случаев, возникающих на практике. Поэтому общепринятые определения сложности задач могут оказаться относительно бессмысленными в терминах реальной сложности, так как две задачи могут быть NP-полными, но одна при этом в большинстве случаев может решаться быстро, а другая нет. Как следствие, важную роль в теории сложности играет понятие «сложности в среднем» (здесь под «средним» понимается математическое ожидание времени решения).
Чтобы проиллюстрировать центральную роль этого понятия, можно вообразить пять различных возможных миров (возможных — потому что еще не доказано, что они нереальны, и наш может оказаться любым из них) и посмотреть как условия в них будут влиять на информатику и жизнь вообще.
В частности, для демонстрации с точки зрения человека, будем использовать печальную историю Профессора Гроуса, того самого преподавателя математики, который задал классу задачку — сосчитать сумму чисел от 1 до 100. Всем известно, что на его беду в классе оказался маленький Гаусс, который быстро заметил закономерности арифметической прогрессии и почти моментально посчитал эту сумму. Но мало кто знает, что после этого Профессором овладела навязчивая идея отомстить Гауссу и унизить его перед всем классом, придумывая задачи, которые Гаусс не мог решить. Это привело Профессора в сумасшедший дом (не самый приятный конец, особенно в 19 веке), а у Гаусса развило интерес к теоретико-числовым алгоритмам. Попробуем представить что было бы в различных мирах, которые будем рассматривать.
Алгоритмика
Алгоритмика — это мир, в котором P = NP. В этом мире Профессору везло бы еще меньше, чем в реальности. Так как Профессору нужно поставить в тупик Гаусса задачей, на которую он (Профессор) затем должен сам показать классу верный ответ, он ограничен в выборе задач теми, которые имеют легко проверяемое решение (то есть задачи из NP). Гаусс может использовать метод проверки, чтобы автоматически решить эту задачу.
Метод автоматического получения алгоритма решения проблем из алгоритма проверки верного решения произведет революцию в информатике того мира. Задачи, которые казались неподдающимися, окажутся тривиальными. Почти все задачи оптимизации будут простыми и автоматическими. Например, в проектировании СБИС больше не будут использоваться эвристики, вместо этого будет генерироваться оптимальная проводка, если задан критерий оптимальности. Языки программирования больше не будут содержать инструкции, описывающие как выполнять вычисления. Вместо этого они только будут описывать свойства, которыми должны обладать выходные данные по отношению к входным данным. Компилятор будет самостоятельно переводить язык спецификаций в алгоритм решения.
Менее очевидно, что P=NP сделает тривиальными многие аспекты программ искусственного интеллекта. Можно будет использовать обучающиеся системы, основывающиеся на принципе «бритвы Оккама», чтобы автоматически обучать компьютер выполнять действия, которые могут делать люди. Достаточно будет обеспечить обучающую выборку входных данных и выходных данных, произведенных человеком-экспертом, и компьютер выведет простейший алгоритм, которые будет выдавать те же ответы, что и эксперт. Так, компьютер можно будет научить распознавать и разбирать предложения на естественном языке, нужно только обеспечить достаточное количество примеров верных и неверных предложений (здесь предполагается, что существует некий простой алгоритм, который люди используют для разбора естественных языков).
С другой стороны, в Алгоритмике не будет возможности различить людей и компьютеры с информационной точки зрения. Упомянутые обучающиеся алгоритмы смогут легко научиться имитировать поведение других машин и даже людей. Любой код, который может быть разработан, так же легко может быть взломан. Мало пользы будет от попыток скрыть алгоритм, на котором основан код, так как такой же алгоритм можно будет легко получить, имея небольшое количество пар шифротекст — плейнтекст. Не будет возможности обеспечить доступ к информации нескольких людям, не делая ее таким образом доступной для всех. Поэтому любые способы идентификации должны будут быть основаны на физических измерениях. И безопасность идентификации будет базироваться на неизменности физических параметров и устойчивости к внешним воздействиям каналов передачи данных от измерителя к идентификационному устройству.
Эвристика
Эвристика — это мир, в котором задачи из NP не имеют эффективных решений в худшем случае, но легко решаемы в среднем (для некоторого распределения вероятностей на множестве входов).
Эвристика, в некотором роде, парадоксальный мир. Здесь существуют сложные экземпляры задач из NP, но найти такой сложный экземпляр — сама по себе сложно решаемая задача. В этом мире Профессор будет иметь возможность найти задачи, которые окажутся не по зубам Гауссу. Но ему придется потратить неделю на поиск задачи, которую Гаусс не сможет решить в течение дня, и год, чтобы найти задачу, на которую Гаусс потратит месяц (в данном случае предполагается, что Гаусс имеет некоторое полиномиальное преимущество над профессором, ведь Гаусс, в конце концов, гений). Скорее всего, жизнь не настолько сурова, чтобы предоставлять нам сложные задачи, лишь бы жизнь малиной не казалась. Поэтому для практических целей этот мир почти неотличим от Алгоритмики.
Или все же отличим? В Эвристике среднее время решения задачи из NP зависит от среднего времени «обдумывания» этой задачи. Это несколько усложняет ситуацию. Допустим, в среднем, вычисление решения задачи в два раза дольше придумывания решения. Если мы тратим время T на обдумывание задачи №1, то мы потратим 2T единиц времени на вычисление решения. Решение этой задачи влияет на решение задачи №2, т.е. на обдумывание решения задачи №2 мы потратили 3Т единиц времени. Поэтому на решение задачи №2 будет потрачено 6Т единиц времени. Что приводит к задаче №3, на обдумывание которой мы уже потратили 10Т единиц времени, следовательно 20Т будет потрачено на решение. Так как эта рекурсия экспоненциально растет, уже через несколько шагов мы пересечем границу между «осуществимым» и «нереальным».
В случае дизайна СБИС здесь уже не обязательно будут эффективные решения, так как в данном случае нас мало интересует большинство возможных подходящих под спецификации схем, а важны минимальные варианты, удовлетворяющие спецификациям. Такие схемы могут не иметь хорошего распределения, и, так как, скорее всего, понадобится экспоненциальное время для их поиска, нет никаких гарантий, что они не являются теми самыми «худшими случаями», на которых плохо работают алгоритмы в Эвристике.
В криптографии и сетевой безопасности не будет принципиальных различий с Алгоритмикой. Мало толку будет, если добросовестные пользователи будут тратить много времени на поиск экземпляра задачи, которая могла бы однозначно их идентифицировать, когда злоумышленник может решить этот экземпляр за сравнимое количество времени (предполагается, что злоумышленник, который хочет взломать систему, использует значительно больше ресурсов, чем добросовестный пользователь).
Пессиландия
Пессиландия — это худший из возможных случаев — в ней есть задачи, решаемые сложно даже в среднем, но нет односторонних функций. Под отсутствием односторонних функций понимается следующее: для любой задачи, которую легко вычислить, также легко найти решение обратной задачи, в том смысле, что для почти всех значений x, если дано F(x), то можно найти некоторый x’, такой, что F(x’) = F(x), причем примерно за то же время, что тратится на вычисление F(x).
В Пессиландии Профессор смог бы задать Гауссу задачки, которые даже молодой гений не смог бы решить. Но и сам Профессор не смог бы продемонстрировать решение, так что унижение Гаусса было бы неполным.
В этом мире во многих областях задачи не имели бы легких решений. Прогресс был бы как и в нашем мире: медленно продвигался бы за счет более глубокого понимания мира и за счет использования не совсем удовлетворительных эвристик. Общие методы решения задач не работали бы в большинстве областей. Однако несколько полезных алгоритмов были бы возможны, базируясь на отсутствии односторонних функций. Например, метод сжатия данных, в котором, зная распределение входных данных, в пределе можно было бы их сжимать до ожидаемой длины в соответствии с энтропией распределения.
В этом мире не будет возможности использовать сложные задачи в криптографии. Задача, на которую никто не знает ответ, не может быть использована для отличия добросовестного пользователя от злоумышленника.
Миникрипт
В Миникрипте есть односторонние функции, но невозможна криптография с открытым ключом. Здесь мы понимаем под криптографией с открытым ключом задачу засекреченного общения через публичные каналы связи, хотя, строго говоря, криптография с открытым ключом — лишь один из способов решения этой задачи.
Односторонние функции могут использоваться для генерации сложных, но решенных задач, а именно: генератор будет выбирать х, вычислять y = F(x) и ставить задачу поиска «найти такой x’, что F(x’) = y». Таким образом, в Миникрипте Профессор, наконец, сможет одержать верх над Гауссом перед всем классом.
В сети участники смогут идентифицировать себя перед другими пользователями, а также удостоверять сообщения с использованием цифровой электронной подписи. Будет возможно доказывать факты о секрете, не открывая другую секретную информацию, содержащуюся в нем. Если небольшое количество информации заранее передано между участниками, то можно установить надежный секретный код между двумя участниками сети, который позволит им общаться в закрытом порядке, используя открытые каналы связи. Однако, невозможно будет провести тайное голосование через открытые каналы, или обеспечить безопасные переговоры, не пересылая заранее некоторую информацию через защищенные каналы. Не будет возможности создать анонимные цифровые деньги.
Криптомания
В Криптомании криптография с открытым ключом существует. В Криптомании Гаусс будет унижен еще больше; Профессор и его ученик-любимчик смогут совместно выбрать задачу, на которую они оба будут знать ответ, а Гаусс ее решить не сможет. Более того, в этом мире Профессор сможет сделать так, что все в классе будут знать как решить заданную задачу, кроме Гаусса.
Из существования протоколов с открытым ключом следует существование односторонних функций, поэтому в этом мире все еще существуют псевдо-случайность, цифровые подписи, идентицикация, протоколы с нулевым знанием и прочее. Также, если засекреченный обмен производится с помощью односторонних функций с секретом (а все известные протоколы явно или косвенно используют именно такие функции), можно решить любые вообразимые криптографические задачи. В отличие от других миров, где создание конфиденциальности — это технологическая задача, технологии в Криптомании наоборот будут ограничивать возможности пользователей к уменьшению конфиденциальности. Большинство решений по тому, сколько конфиденциальности позволено гражданам, будут приниматься в результате политических и социальных процессов, а не из-за технических возможностей.
Этот мир больше всего похож на наш с вами., по крайней мере до тех пор, пока считается, что известные протоколы с открытым ключом надежны.
R. Impagliazzo, «A personal view of average-case complexity,» sct, pp.134, 10th Annual Structure in Complexity Theory Conference (SCT’95), 1995
NP-полная задача
В теории алгоритмов NP-полная задача — задача из класса NP, к которой можно свести любую другую задачу из класса NP за полиномиальное время. Таким образом, NP-полные задачи образуют в некотором смысле подмножество «самых сложных» задач в классе NP; и если для какой-то из них будет найден «быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
Содержание
Формальное определение
Алфавитом называется всякое конечное множество символов (например, 







Задачей распознавания для языка 

Язык 


Сводимость по Карпу обозначается как 

Язык 
Таким образом, если будет найден алгоритм, решающий некоторую (любую) NP-полную задачу за полиномиальное время, то все NP-задачи окажутся в классе P, то есть будут решаться за полиномиальное время.
NP-полнота в сильном смысле
Задача называется NP-полной в сильном смысле, если у неё существует подзадача, которая:
Класс таких задач называется NPCS. Если гипотеза P ≠ NP верна, то для NPCS задачи не существует псевдополиномиального алгоритма.
Гипотеза P ≠ NP
Вопрос о совпадении классов P и NP уже более 30 лет является открытой проблемой. Научное сообщество склоняется к отрицательному ответу на этот вопрос [1] — в этом случае решать NP-полные задачи за полиномиальное время не удастся.
Примеры NP-полных задач
См. также
Примечания
Литература
Ссылки
| Cчитаются лёгкими | P • L • NL • AC • NC • P-complete • BQP • BPP • RP • ZPP |
|---|---|
| Предпологаются сложными | NP (co-NP • NP-complete • co-NP-complete ) • UP • #P (#P-complete ) • IP • PSPACE (PSPACE-complete) • R • PP • AM |
| Cчитаются сложными | EXPTIME • NEXPTIME • EXPSPACE • 2-EXPTIME • PR • RE • Co-RE • RE-complete • Co-RE-complete • PH |
| Список алгоритмов | |
 NP-полные задачи NP-полные задачи | |
|---|---|
| Математика | |
| Исследование операций:Оптимизация:Комбинаторная оптимизация | |
| Максимизационная задача укладки (упаковки) | Упаковка в контейнеры (двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости) • Задача о ранце (рюкзаке) |
| Теория графов теория множеств | Задача о вершинном покрытии • Задача о клике • Задача о независимом множестве (наборе) • Задача о покрытии множества • Задача Штейнера • Задача коммивояжёра • Обобщённая задача коммивояжёра |
| Алгоритмические задачи | Задача выполнимости булевых формул (в конъюнктивной нормальной форме) |
| Логические игры и головоломки | Обобщённые пятнашки с костяшками >15) (задача поиска кратчайшего решения) • Задачи, решения которых применяются в Тетрис • Задача обобщённого судоку • Задача о заполнении латинского квадрата • Задача какуро |
| См. также | Прикладная математика • Теория алгоритмов • Динамическое программирование • 21 NP-полная задача Карпа |
| Классы сложности | |
Полезное
Смотреть что такое «NP-полная задача» в других словарях:
AI-полная задача — AI полная задача, по аналогии с NP полным классом задач в теории сложности, термин, предложенный Ф. С. Монталво[где?] для обозначения того факта, что сложность данной компьютерной задачи эквивалентна главной проблеме… … Википедия
21 NP-полная задача Карпа — Список Карпа список, состоящий из формулировки и доказательства NP полноты 21 задачи, опубликованный Ричардом Карпом в 1972 году в своем труде «Возможность редукции в комбинаторных задачах» (англ. «Reducibility Among Combinatorial Problems») … Википедия
Задача о вершинном покрытии — NP полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP полноты более сложных задач. Содержание 1 Определение 2 NP полнота 3 Ссылки … Википедия
Задача о покрытии множества — является классическим вопросом информатики и теории сложности. Данная задача обобщает NP полную задачу о вершинном покрытии (и потому является NP сложной). Несмотря на то, что задача о вершинном покрытии сходна с данной, подход, использованный в… … Википедия
Задача SAT — Задача выполнимости булевых формул (SAT или ВЫП) задача распознавания, важная для теории вычислительной сложности. Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций (И), (ИЛИ) и (HE). Задача… … Википедия
Задача ВЫП — Задача выполнимости булевых формул (SAT или ВЫП) задача распознавания, важная для теории вычислительной сложности. Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций (И), (ИЛИ) и (HE). Задача… … Википедия
Задача о независимом множестве — относится к классу NP полных задач в области теории графов. Эквивалентна задаче о клике. Содержание 1 Определения 2 Максимальное независимое множество в дереве … Википедия
Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия