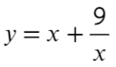Что такое min в математике
Комплексные упражнения с функциями вида y = min f (x); g(x) или y = max f (x); g(x)
Разделы: Математика
В статье предлагается подборка комплексных упражнений, которые содержат функции вида: y=min
Привлекательность и полезность этих упражнений состоит в том, что, приступая к их решению, учащиеся часто теряются и не могут понять, по какой теме работать. Комплексные упражнения объединяют несколько тем из курса математики (уравнения, неравенства, графики), причем учат обращать внимание на “тонкости” при тождественных преобразованиях, после которых задание становиться достаточно простым.
Такие комплексные задания дают на олимпиадах, на экзаменах в различные вузы страны, в заданиях ЗФТШ при МФТИ и даже в “заданиях для проведения письменного экзамена по математике в 9 кл.” авторов Л.И. Звавича, Д.И. Аверьянова, Б.П. Пигарева, Т.Н. Трушаниной.
Статья рассчитана на учителей математики, на учащихся специализированных математических классов и лицеев физико-математического профиля, а также для обычных классов при подготовке к олимпиадам и для поступления в вузы.
Знакомство с комплексными упражнениями, которые содержат функции y=min
Из методички ЗФТШ при МФТИ по теме: “Функции и их графики”
Из “Решения задач повышенной сложности” автор С.Л. Евсюк.
Решая четные неравенства, получаем x = 1/2.
Из “Сборника заданий для проведения письменного экзамена по математике в 9 кл.”
Авторы Л.И. Звавич, Д.И. Аверьянов, Б.П. Пигарев, Т.Н. Трушанина.
Пусть max
2.250. а) max <





2.251. а) min <





Решение этих заданий
2.250. а) Найдите все x, для которых max <






Ответ: 
2.251 а) Найти все x, для которых min<


Достаточно найти все x, удовлетворяющие хотя бы одну из систем:

Ответ: x 

2.252 а) Найти все x, для которых
Ответ: x=4 или
Выясним сначала, когда x


Ответ:
Из пособия “Комплексные упражнения по математике с решениями 7–11 классы”
Из задачника “Начала анализа” авторы В.В. Вавилов, И.И. Мельников, С.Н. Олехник, П.И. Пасиченко.
Самостоятельно: построить графики:
Что такое min в математике
Значения функции и точки максимума и минимума

Наменьшее значение функции
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
Найти точку максимума / минимума
Найдите точку максимума функции
Найдите точку минимума функции
Найти наибольшее / наименьшее значение функции
Найдите наибольшее значение функции на отрезке [−4; −1]
Найдите наибольшее значение функции на отрезке [0; 1,5π]
Как вы рассчитываете минимум?
Кроме того, каков максимум по математике?
Максимум, по математике, точка, в которой значение функции наибольшее. Если значение больше или равно всем другим значениям функции, это абсолютный максимум. … В исчислении производная равна нулю или не существует в точке максимума функции.
Итак, как вы рассчитываете Макс?
Также нужно знать, какое минимальное значение в математике? Минимум по математике, точка, в которой значение функции меньше или равно значению в любой соседней точке (локальный минимум) или в любой точке (абсолютный минимум); см. экстремум.
Как рассчитать среднее значение?
Среднее или среднее значение рассчитывается путем сложения баллов и деления общей суммы на количество баллов.. Рассмотрим следующий набор чисел: 3, 4, 6, 6, 8, 9, 11.
Какой минимальный и максимальный срок?
A минимальный срок хранения говорит вам, как долго вы должны хранить данные как минимум. … Максимальный срок хранения указывает, когда следует уничтожить определенную запись. По истечении этого периода у вас действительно больше не должно быть записи. Пора с этим попрощаться.
Какой символ минимума?
Для упорядочивания минимальное значение означает «меньше или равно», что в некоторых / многих математических дисциплинах обозначается как ≤. На самом деле символ имеет два значения.
Что такое максимальное и минимальное значение?
Какой процент составляет 3 повторения?
Процент повторений 1ПМ
| Повторения | Процент от 1ПМ |
|---|---|
| 2 | 97% |
| 3 | 94% |
| 4 | 92% |
| 5 | 89% |
Как я могу рассчитать среднее значение?
Среднее значение равно сумме набора чисел, разделенной на количество, которое является количеством добавляемых значений.. Например, вы хотите получить среднее значение 13, 54, 88, 27 и 104. Найдите сумму чисел: 13 + 54 + 88+ 27 + 104 = 286. В нашем наборе данных пять чисел, поэтому разделите 286 на 5, чтобы получить 57.2.
Точен ли калькулятор 1ПМ?
Что касается точности калькулятора максимума одного повторения; формулы на большинстве калькуляторы довольно точны до и около отметки в 5 повторений. Калькуляторы, которые пытаются предсказать, какой будет ваш максимум 10,15 или 20 повторений на основе вашего максимального количества повторений, совсем не надежны.
Что означает min XY?
В этом вопросе min (x, y) означает на меньшее из двух перечисленных значений, x и y. С другой стороны, max (x, y) относится к большему из двух значений в скобках.
Что означает min <> в математике?
Наименьшее значение. Минимум <14, 4, 16, 12>равен 4.
Какова формула выборочного среднего?
Вычислить выборочное среднее так же просто, как сложить количество элементов в выборочном наборе и затем разделить эту сумму на количество элементов в выборочном наборе. Чтобы вычислить выборочное среднее значение с помощью программного обеспечения для работы с электронными таблицами и калькуляторов, вы можете использовать формулу: x̄ = (Σ xi) / n.
Какова формула для режима сгруппированных данных?
Какая формула для среднего?
Среднее арифметическое, рассчитываемое по формуле добавление группы чисел и последующее деление на количество этих чисел. Например, среднее значение 2, 3, 3, 5, 7 и 10 равно 30, разделенному на 6, что равно 5.
Какой максимальный срок?
Продолжительность менструального цикла варьируется от женщины к женщине, но в среднем менструация должна быть каждые 28 дней. Регулярные циклы, которые длиннее или короче, чем это, от 21 в 40 дней, нормальные.
Какой максимальный срок?
Хотя средний цикл длится 28 дней, от 21 до 45 дней считается нормальным. Это разница в 24 дня. В первые год или два после начала менструации у женщин, как правило, бывают более длинные циклы, которые не начинаются в одно и то же время каждый месяц. У пожилых женщин циклы обычно короче и стабильнее.
Что такое максимальное удержание?
Определение: Максимальный размер риска, сохраняемого страховщиком в течение жизни называется удержанием. Кроме того, страховщик передает перестраховщику избыточный риск. Точка, после которой страховщик уступает риск перестраховщику, называется лимитом удержания.
Не меньше знака?
Меньше символа Что такое MIN () в математике?
Минимум по математике, точка, в которой значение функции меньше или равно значению в любой соседней точке (локальный минимум) или в любой точке (абсолютный минимум); см. экстремум. Связанные темы: Экстремум. Эта статья была недавно отредактирована и обновлена Уильямом Л.
Какая минимальная точка?
Может быть 2 абсолютных максимума?
Важно: хотя функция может иметь только одно абсолютное минимальное значение и только одно абсолютное максимальное значение (в указанном закрытом интервале) он может иметь более одного местоположения (значения x) или точек (упорядоченные пары), где встречаются эти значения.
Как узнать, является ли вершина максимумом или минимумом?
Если парабола открывается, вершина представляет собой самую низкую точку на графике, или минимальное значение квадратичной функции. Если парабола раскрывается вниз, вершина представляет собой наивысшую точку на графике или максимальное значение.
Как найти глобальный максимум и минимум?
Затем, чтобы найти глобальный максимум и минимум функции:
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Основные определения
Начнем, как всегда, с формулировки основных определений.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
Наибольшее и наименьшее значение функции на открытом интервале
Наибольшее и наименьшее значение функции на бесконечности
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Решение:
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
Следовательно, производные функции существуют на всей области ее определения.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.