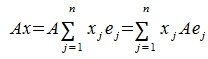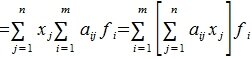Что такое lin математика

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Рубрика: Линейная алгебра

Линейная алгебра – это раздел математики, в рамках которого изучаются самые разнообразные объекты линейной природы. В числу таких объектов относят линейные уравнения и пространства, отображения и т.д.

Основным объектом линейной алгебры является линейное пространство — понятие, обобщающее:

Элементы линейного пространства называют векторами, обобщая термин из векторной алгебры. Само линейное пространство часто называют векторным.

Линейные пространства — один из самых распространенных математических объектов, и применение линейной алгебры далеко не исчерпывает векторной и матричной алгебрами.

В линейном пространстве действуют две операции:

Однако могут вводиться и другие операции и соответственно дополнительные аксиомы. Эти операции задают дополнительные отношения в линейном пространстве, которые тоже изучаются в линейной алгебре и часто используются в различных приложениях.

Среди базовых инструментов линейной алгебры можно назвать матрицы и определители, а также сопряжение. В разделе «Линейная алгебра» на нашем сайте можно найти основные определения, кроме того, примеры с подробным решением, а также видеоуроки. Если не нашли нужную тему, или есть трудности с решением каких-то типовых задач — пишите об этом в комментариях.

Перечень тем курса линейной алгебры

Ранг матрицы

Рангом матрицы А называется наибольший из порядков ее миноров, не равных нулю. Обозначается ранг матрицы: r(A) или rang(A). Методы нахождения ранга матрицы Суще.

Правило треугольника

Общая формула вычисления определителя матрицы 3 на 3 довольно громоздка. Поэтому для вычисления определителя 3 порядка существует метод под названием — пр.

Метод Жордана — Гаусса

Этот метод заключается в следующем: расширенную матрицу системы путем элементарных преобразований нужно привести к ступенчатому виду. К элементарным преобразова.

Источник

Линейная алгебра: пробный заезд

Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.

Часто первое знакомство с линейной алгеброй выглядит как-то так:

Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.

Начнем с практики

Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:

Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.

Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:

где Q_x-h — поток тепла через левую границу, а Q_x+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)

где мы уже учли граничные условия, а q_i=q(x_i). Ну вот мы и получили систему линейных уравнений:

В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:

где a_ij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:

Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.

Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.

Теперь немного теории

Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(α · x + β · y) = α · f(x) + β · f(y) для любых чисел α и β и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.

В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.

Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.

Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)

Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.

Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?

Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.

Википедия Книга — лучший источник знаний

Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.

Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.

Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.

Источник

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

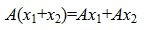,	(2)
.

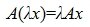Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Источник