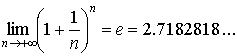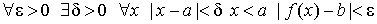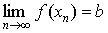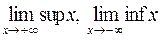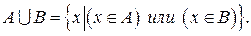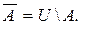Что такое inf и sup в математике
Точные грани числовых множеств
Верхняя и нижняя грани числовых множеств.
Множество X вещественных чисел (X ⊂ \(\mathbb
$$
\exists C \ \in \ \mathbb
$$
Всякое вещественное число C, обладающее свойством \eqref
Аналогично, множество X ⊂ \(\mathbb
$$
\exists C’\in\mathbb
$$
Всякое вещественное число С ‘ , удовлетворяющее условию \eqref
Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb
Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb
По условию \(B=\left\<\exists C \ \in \ \mathbb
$$
\rceil B=\left\<\forall C \ \in \ \mathbb
Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:
Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.
Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.
Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:
Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.
Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:
Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref
Возьмем произвольное число x ∈ X и пусть x = a0,<an>. Чтобы проверить выполнение условия \eqref
$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label
$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label
$$\exists m: \ x\in X_
Из \eqref
Из неравенства \eqref
1. Теория пределов
1.1 Супремум и инфимум
Определение 1. Множество < x >, элементами которого являются числа, называется числовым множеством.
Определение 2. Множество вещественных чисел < x > называется ограниченным сверху (снизу), если существует число M ( m ) такое, что 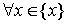
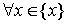
Число M называется верхней гранью числового множества < x >. Аналогично, число m называется нижней гранью числового множества < x >.
Верхних (нижних) граней бесконечно много, так как любое число, большее M (меньшее m ), есть также верхняя (нижняя) грань.
Определение 3. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества < x > (обозначение sup < x >).
Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества < x > (обозначение inf < x >).
Более точно, эти понятия выражаются следующими свойствами:
1. 
2. 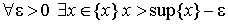
1. 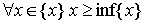
2. 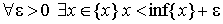
Теорема о существовании супремума и инфимума числового множества.
Если числовое множество < x > не пусто и ограничено сверху, то у него существует sup < x >.
Если числовое множество < x > не пусто и ограничено снизу, то у него существует inf < x >.
1.2 Последовательности
Определение 1. Числовой последовательностью (в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел
Обратите внимание на два момента.
1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!
2. Все числа упорядочены, то есть расположены в определенном порядке.
В дальнейшем для последовательности часто будем использовать сокращенное обозначение < xn >.
Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них.
1. Умножение последовательности на число.
Последовательность c × < xn > – это последовательность с элементами < c × xn >, то есть
2. Сложение и вычитание последовательностей.
или, более подробно,
3. Умножение последовательностей.
4. Деление последовательностей.
Естественно, предполагается, что в этом случае все yn ¹ 0.
Последовательность < xn > называется ограниченной сверху, если 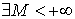
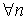
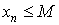
Последовательность < xn > называется ограниченной снизу, если 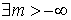
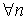
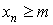
Последовательность < xn > называется ограниченной, если она одновременно ограничена и сверху и снизу.
1.3 Предел последовательности.
Основное определение. Число a называется пределом последовательности < xn > при n стремящимся к бесконечности, если
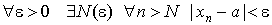
Для этого факта используют следующие обозначения:
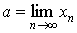
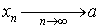
Говорят, что 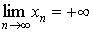
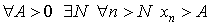
Говорят, что 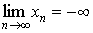
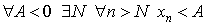
Последовательность < xn > называется бесконечно большой, если 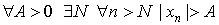
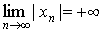
1.4 Бесконечно малые последовательности.
Оределение. Последовательность < xn > называется бесконечно малой, если 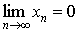

Бесконечно малые последовательности имеют следующие свойства.
1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.
2. Бесконечно малая последовательность ограничена.
3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
1.5 Сходящиеся последовательности.
Определение. Если существует конечный предел 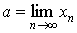
Сходящиеся последовательности имеют следующие свойства.
1. Сходящаяся последовательность ограничена.
2. 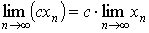
3. 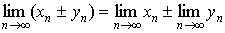
4. 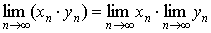
5. Если 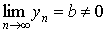
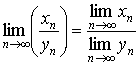
1.6 Предельный переход в неравенствах.
1. 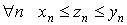
2. 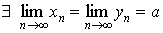
то существует 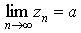
1.7 Предел монотонной последовательности.
Последовательность < xn > называется монотонно возрастающей, если для любого n xn +1 ³ xn .
Последовательность < xn > называется строго монотонно возрастающей, если для любого n xn +1 > xn .
Последовательность < xn > называется монотонно убывающей, если для любого n xn +1 £ xn .
Последовательность < xn > называется строго монотонно убывающей, если для любого n xn +1 xn .
Теорема о существовании предела монотонной последовательности.
1. Если последовательность < xn > монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup < xn > ( inf < xn > ).
На основании этой теоремы доказывается, что существует так называемый замечательный предел
1.8 Подпоследовательности
и рассмотрим последовательность 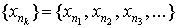
Если < xn > – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.
Лемма Больцано- Вейерштрасса.
1. Из любой ограниченной последовательности можно извлечь такую подпоследовательность, которая сходится к конечному пределу.
2. Из любой неограниченной последовательности можно извлечь бесконечно большую подпоследовательность.
На основании этой леммы доказывается один из основных результатов теории пределов –
Признак сходимости Больцано-Коши.
Для того, чтобы у последовательности < xn > существовал конечный предел, необходимо и достаточно, чтобы
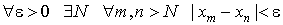
Последовательность, удовлетворяющая этому свойству, называется фундаментальной последовательностью, или последовательностью, сходящейся в себе.
1.9 Предел функции
Основное определение. Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к a (обозначение 
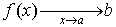
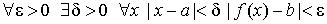
Число b называется предельным значением (пределом) функции f ( x ) при x стремящимся к + ¥ (обозначение 

Говорят, что функция f ( x ) стремится к + ¥ при x стремящимся к a (обозначение 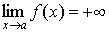
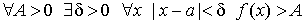
( 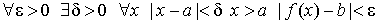
Обозначение 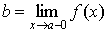

Если 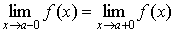
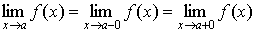
Теорема, устанавливающая связь понятий предела функции и предела последовательности.
Для того, чтобы существовал 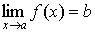
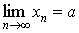
Свойства предельных значений.
Предельные значения имеют такие же свойства, что и предел последовательности:
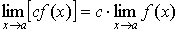
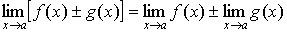
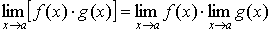
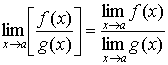
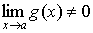
1.10 Предел монотонной функции
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1)> f ( x 2).
Функция f ( x ) называется
строго монотонно возрастающей, если из x 1> x 2 следует f ( x 1) f ( x 2).
Если f ( x ) при x a и ограничена сверху то существует конечный 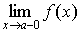
Если f ( x ) при x a но сверху не ограничена, то 
Аналогичные формулировки имеют место и для монотонно убывающей функции.
1.11 Признак Больцано-Коши существования предела функции.
Теорема. Для того, чтобы при x стремящимся к a существовал конечный 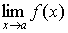
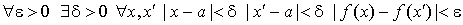
Эта теорема является одной из важнейших теорем теории пределов.
1.12 Сравнение бесконечно малых и бесконечно больших величин
1. Если существует 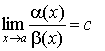
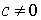
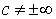
Обозначение: a = O ( b ) или b = O ( a ).
2. Если 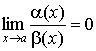
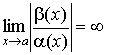
Обозначение a = o ( b ).
3. Если 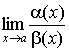
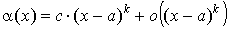
Слагаемое 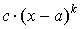
1. Если существует 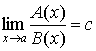
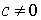
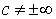
2. Если 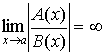
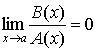
3. Если 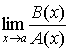
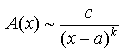
Понятие о верхней и нижней гранях множеств
При рассмотрении числовых множеств часто возникает необходимость установления их граничных значений. Если множество задано перечислением его элементов, то это делается без особого труда путем выделения его минимального и максимального значений. Например, для множества X = <0, 1, 2, 4, 8>min x = 0, max x = 8.
Если же множество задано в «форме от х», то указать минимальное и максимальное его значения не всегда оказывается просто, а иногда они и не существуют. Например, для множества N натуральных чисел минимальным числом является единица. А максимальное число не существует. Для множества Z целых чисел не существует ни минимума, ни максимума.
Для рассмотренного выше множества X = <0, 1, 2, 4, 8>очевидно, что
min X = inf X = 0, max X = sup X = 8. Однако для неограниченного сверху множества N натуральных чисел min N = inf N = 1, а max N не существует, но sup N = + 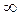
Приведенные примеры возможно не очень убедительны, так как использование символов – 
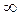
Например, для отрезка 1 ≤ х ≤ 3 при х 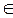
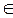
Чисел, которые могут рассматриваться в качестве верхней или нижней граней множества, может быть бесконечно много. Для устранения такой неоднозначности введено понятие точной верхней и точной нижней граней множества. Под точной верхней гранью множества Х понимают такую верхнюю грань, которая не превосходит любую другую. Под точной нижней гранью множества Х, понимают такую нижнюю грань, которая не меньше любой другой грани.
Исходя из приведенных определений, символически точные верхние и нижние грани множества, если его представлять в виде последовательности действительных чисел, можно записать через верхний и нижний пределы: 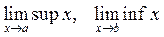
для бесконечных множеств.
Однако чтобы не перегружать символикой понятия точной верхней и нижней граней пределы опускают и в качестве точной верхней и нижней граней принимают соответственно sup X и inf X.
Наконец, следует отметить, что всякое непустое множество действительных чисел имеет, и притом единственную, верхнюю и нижнюю конечную или бесконечную грани.
Операции над множествами.
Над множествами можно выполнять определенные операции, подобные в некотором отношении операциям над действительными числами в алгебре. Поэтому можно говорить об алгебре множеств.
Объединением (соединением) множеств А и В называется множество (символически оно обозначается через 
Запись 
Операции над множествами наглядно изображают графически с помощью кругов Эйлера (иногда используют термин «диаграммы Венна-Эйлера»). Если все элементы множества А будут сосредоточены в пределах круга А, а элементы множества В – в пределах круга В, тооперацию объединения с помощью кругов Эйлера можно представить в следующем виде – рис. 2.1
Рис. 2.1. Объединение множеств А и В
Пример 1. Объединением множества А = <0, 2, 4, 6, 8>четных цифр и множества В = <1, 3, 5, 7, 9>нечетных цифр является множество 
Пример 2. Если A = <1, 2, 3>, B = <2, 3, 4>, то 
Пример 3. Объединением множеств А = <1>и B = <0, 1>решений квадратных уравнений х 2 + 2х + 1 = 0 и х 2 + х = 0 является множество 
Пример 4. Пусть А1 = <3,6,9>, A2= <0,1,5,7>, A3= <2,3,4,5,8>, тогда 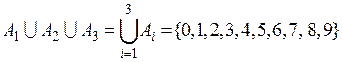
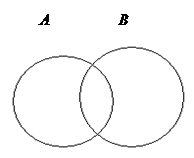
Пересечением (произведением) множеств А и В называется множество (обозначается через 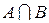
В форме от х пересечение множеств записывается так
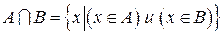
Запись 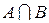
Рис. 2.2. Пересечение множеств А и В
Если 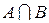
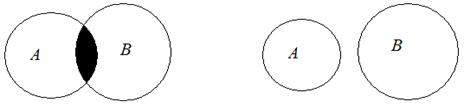
Разностью множеств А и В называется множество (обозначается А\В или А – В), состоящее из всех тех элементов множества А, которые не являются элементами множества В. В «форме от х» разность множеств А и В можно записать так
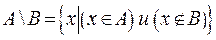
Выражение А\В читается: «разность А и В» или «А без В».
Разность множеств в отличие от предыдущих операций определяется только для двух множеств.
С помощью кругов Эйлера для множеств А и В разности А\В и В\А в виде затемненных частей кругов приведены соответственно на рис. 2.3 а, и 2.3 б
Рис. 2.3. Разности множеств А\В и В\А
Пример 6. Пусть А = <0, 2, 4, 6, 8>– множество всех четных цифр, В = <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>– множество всех цифр десятичной системы счисления. Тогда В\А = <1, 3, 5, 7, 9>всех нечетных цифр является разностью множеств В и А.
Для случая, когда 
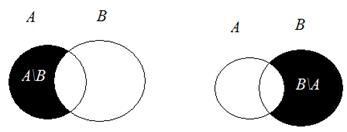
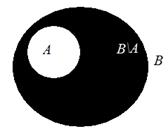
Дополнением множества А до множества В называется множество, всех тех элементов множества В, которые не принадлежат множеству А. С помощью кругов Эйлера множество-дополнение в затемненном виде представлено на рис. 2.4
Рис. 2.4. Подмножество В\A – дополнение множества А до множества В
Символически операция дополнения записывается также как и операция разности, поэтому в «форме от х»запись дополнения будет иметь вид

Если в процессе некоторого рассуждения все рассматриваемые множества являются подмножествами некоторого множества U, то это множество называют универсальным множеством (или для краткости – универсумом). Рассуждение может быть не только кратким, но и представлять научную теорию или целую книгу. Например, при проведении социологических исследований в качестве универсума могут рассматриваться все города России или все студенты некоторого вуза. В первом случае все рассуждения не могут выходить за рамки всех городов, а во втором – за рамки всех студентов этого вуза.
Для графической иллюстрации отношений между подмножествами какого-либо ограниченного универсального множества U круги Эйлера, отображающие подмножества множества U, ограничивают прямоугольником – рис. 2.5
Рис. 2.5. Универсальное множество U и его подмножества A и B
Ясно, что если в некотором рассуждении универсальное множество будет неограниченным, например множество N или Z,то ограничить его
прямоугольником не представляется возможным.
Если в рассуждениях участвуют универсальное множество U и некоторое подмножество A, то подмножество 

Тогда приведенное выше определение дополнения множества A до множества B называют относительным.
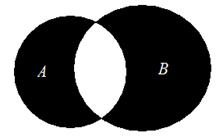
Кроме приведенных операций над множествами рассматривают еще две – операцию симметрической разности и операцию сложения множеств. Симметрической разностью (обозначается 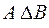
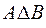
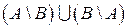
С помощью кругов Эйлера симметрическая разность множества А (левый полный круг)и множества В (правый полный круг)на рис. 2.6 будет представлять затемненную часть
Рис. 2.6. Симметрическая разность множеств А и В
Суммой множеств А и В (обозначается А + В) называется множество, определяемое выражением
А + В = ( 

Исходя из приведенной записи для операции сложения, можно сказать, что сумма множеств равна их объединению без пересечения.
Симметрическая разность множеств А и В и их сумма представляют одно и то же множество. Покажем это, используя круги Эйлера.
По определению разность множеств А и В или относительное дополнение А\В являются подмножеством, изображенным на рис. 2.7 а (на рис. 2.3 а это левая затемненная часть круга Эйлера). Разность множеств В и А или относительное дополнение В\A является подмножеством, изображенным на рис. 2.7 б (на рис. 2.3 б это правая затемненная часть круга Эйлера)
Объединяя эти подмножества, мы получаем фигуру, приведенную на рис. 2.6, которая представляет по определению симметрическую разность множеств А и В, т.е. 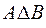
С другой стороны, если мы объединим множества А и В, то получим правую фигуру, т.е. 
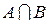
Таким образом, мы доказали с помощью кругов Эйлера, что
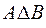
Рассмотрим примеры выполнения операций вычитания, дополнения, сложения и симметрической разности для различных случаев задания множеств.
Пример 8. Пусть заданы множества: А = <2, 3>; B = <1, 2, 3, 4, 5>; C = = <1, 2, 3>; D = <3, 4, 5>. Тогда
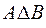



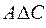



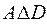

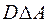

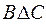

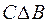
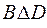


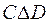

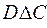
Из приведенных примеров видно, что операции сложения и симметрической разности эквивалентны и обладают свойством коммутативности.