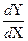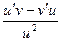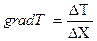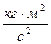Что такое grad в физике

Значение слова «градиент»

[От лат. gradiens, gradientis — шагающий]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Например, если взять в качестве

высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

С математической точки зрения на градиент можно смотреть как на:

1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента

2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных

3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных

Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).

Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.

Источник

Град (единица измерения)

Град (гон), метрическая минута, метрическая секунда — единицы измерения плоских углов.

Исторически плоские углы измеряли в градусах, минутах и секундах. Однако эта непозиционная система была неудобна для практических расчётов, поэтому в конце XVIII века во Франции при введении метрической системы мер в качестве основной единицы измерения плоских углов был предложен град (фр. grade — вариация слова gradus). Название гон (gon — от греч. γονία — угол) используется в Германии, Швеции и некоторых других странах северной Европы.

Связь града с другими единицами

Соотношение града с другими единицами измерения углов описывается формулой:

По аналогии с разбиением градуса на минуты и секунды град разбивают на метрические минуты ( c ) и секунды ( cc ) — в граде 100 метрических минут, в минуте — 100 секунд.

В настоящее время грады практически не используются, хотя возможность их применения часто закладывается в микрокалькуляторах.

См. также

Полезное

Смотреть что такое «Град (единица измерения)» в других словарях:

Град (единица измерения) — Град, гон, единица измерения плоского угла, предложенная при введении метрической системы мер (конец 18 в.). Сокращённое обозначение 1g. 1 Г. равен 1/100 прямого угла. Дольные единицы Г.: метрическая минута (1 или 1c ), равная 1/100 града, и… … Большая советская энциклопедия

ГОН (единица измерения) — ГОН (единица измерения), см. Град (см. ГРАД (в математике)) … Энциклопедический словарь

Секунда единица измерения — шестидесятая доля угловой минуты или минуты времени. Сутки содержат 86400 С. О различии звездной и средней С. см. Время. Названия С. и минуты произошли от сокращения выражений: partes minutae primae, partes minutae secundae. С. дуги обозначается… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Секунда, единица измерения — шестидесятая доля угловой минуты или минуты времени. Сутки содержат 86400 С. О различии звездной и средней С. см. Время. Названия С. и минуты произошли от сокращения выражений: partes minutae primae, partes minutae secundae. С. дуги обозначается… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Секунда (единица измерения плоских углов) — Градус, минута, секунда общепринятые единицы измерения плоских углов и земного шара. Содержание 1 Градус 2 Минуты и секунды 3 Угловая секунда 3.1 Исполь … Википедия

Секунда (единица измерения углов) — Градус, минута, секунда общепринятые единицы измерения плоских углов и земного шара. Содержание 1 Градус 2 Минуты и секунды 3 Угловая секунда 3.1 Исполь … Википедия

Град (значения) — В Викисловаре есть статья «град» Град: Град то же, что и город или городище. Град вид атмосферных осадков в виде льда. Град единица измерения плоских углов. «Град» политическая группировка в Чехии. «Град»& … Википедия

измерения в психологии — (измерения в психологии) процедуры определения количественной выраженности психологических феноменов. В них применяются разнообразные шкалы, содержащие некое множество позиций, поставленных в некое соответствие с психологическими элементами … Большая психологическая энциклопедия

ГРАД — (1. Hail, 2. Grade) 1. Атмосферные осадки, выпадающие в виде кусочков льда (градин) большей частью округлой или яйцевидной формы. Выпадение Г. наблюдается чаще всего в средних широтах; оно бывает главным образом в теплое время года при грозах или … Морской словарь

град — grade, degré centigrade. Градус, единица измерения. Лекс. Геод. сл.: град … Исторический словарь галлицизмов русского языка

Источник

СОДЕРЖАНИЕ

Мотивация

Обозначение

Определение

Когда функция также зависит от параметра, такого как время, градиент часто относится просто к вектору только его пространственных производных (см. Пространственный градиент ).

Декартовы координаты

В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, задается следующим образом:

Цилиндрические и сферические координаты

В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:

В сферических координатах градиент определяется как:

Общие координаты

Последнее выражение соответствует приведенным выше выражениям для цилиндрических и сферических координат.

Связь с производной

Связь с полной производной

С вычислительной точки зрения, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что равносильно взятию скалярного произведения с градиентом:

( d f p ) ( v ) = [ ∂ f ∂ x 1 ( p ) ⋯ ∂ f ∂ x n ( p ) ] [ v 1 ⋮ v n ] = ∑ i = 1 n ∂ f ∂ x i ( p ) v i = [ ∂ f ∂ x 1 ( p ) ⋮ ∂ f ∂ x n ( p ) ] ⋅ [ v 1 ⋮ v n ] = ∇ f ( p ) ⋅ v <\displaystyle (df_

)(v)=<\begin<\frac <\partial f><\partial x_<1>>>(p)&\cdots &<\frac <\partial f><\partial x_>>(p)\end><\beginv_<1>\\\vdots \\v_\end>=\sum _^<\frac <\partial f><\partial x_>>(p)v_=<\begin<\frac <\partial f><\partial x_<1>>>(p)\\\vdots \\<\frac <\partial f><\partial x_>>(p)\end>\cdot <\beginv_<1>\\\vdots \\v_\end>=\nabla f(p)\cdot v>

Дифференциальная или (внешняя) производная

Наилучшее линейное приближение дифференцируемой функции

Градиент связан с дифференциалом формулой

Если R n рассматривается как пространство векторов-столбцов (размерности n ) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами

Линейное приближение к функции

f ( x ) ≈ f ( x 0 ) + ( ∇ f ) x 0 ⋅ ( x − x 0 ) <\displaystyle f(x)\approx f(x_<0>)+(\nabla f)_>\cdot (x-x_<0>)>

Связь с производной Фреше

Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:

Другие свойства и применения

Наборы уровней

В более общем смысле, любая вложенная гиперповерхность в римановом многообразии может быть вырезана уравнением вида F ( P ) = 0 таким, что dF нигде не равно нулю. Тогда градиент F нормален к гиперповерхности.

Консервативные векторные поля и градиентная теорема

Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы (основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.

Обобщения

Якобиан

Градиент векторного поля

Поскольку полная производная векторного поля является линейным отображением векторов в векторы, это тензорная величина.

(где используется обозначение суммирования Эйнштейна, а тензорное произведение векторов e _i и e _k является диадическим тензором типа (2,0)). В целом это выражение равно транспонированной матрице Якоби:

В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :

Выражаясь более инвариантно, градиент векторного поля f может быть определен связностью Леви-Чивиты и метрическим тензором:

Римановы многообразия

где X j обозначает j- й компонент X в этой координатной карте.

Итак, локальная форма градиента принимает вид:

Источник

Градиент функции

Рисунок 3.

Приращение функции – изменение функции.

у

А В

Производной функциейназывается предел отношения приращения функции к приращению аргумента при последнем, стремящемся к нулю.

y’= lim =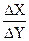

Процесс вычисления производной называется дифференцированием.

Дифференциалом функции → y = f(x) называется dy = y’dx, где dx – произвольное приращение аргумента.

y’=

Интегрирование – процесс обратный дифференцированию.

Основные свойства производной:

()’=

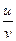
Градиентом физической величины называется отношение приращения этой функции к расстоянию, на котором это приращение происходит. Градиент физической величины – величина векторная и направлена в сторону увеличения значений этой величины.

● ●

Физической величиной называют все то, что можно измерить количественно. Физические величины бывают векторные и скалярные.

Векторные величины, кроме численного значения, имеют еще и направление. Скалярные величины имеют только численные значения.

Для получения числовых значений физических величин необходимо измерять эти физические величины. Измерение физической величины сводится к сравнению её с однородной физической величиной, принятой за единицу. Для каждой физической величины эту единицу можно выбирать произвольно. Однако на практике для удобства выбраны единицы только для семи физических величин, называемых основными. Единицы всех остальных физических величин устанавливают на основании законов, связывающих эти величины с основными. Совокупность всех единиц измерения физических величин называется системой единиц.

Международная система единиц «СИ»

7. Количество вещества моль

1. Плоский угол рад

2. Телесный угол срад

Все остальные являются производными.

[H] = 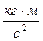; [Дж] =

Измерить физическую величину, значит сравнить ее с единицей измерения (эталоном).

Источник

Что такое grad в физике

← →
Romkin © ( 2004-09-10 10:09 ) [1]

Градиент. Вектор, направленный в сторону наиболшего возрастания функции в данной точке. Его длина указывает скорость этого возрастания. Примечание: ручей с холма всегда течет обратно градиенту в любой своей точке.

← →
Думкин © ( 2004-09-10 10:11 ) [2]

> [1] Romkin © (10.09.04 10:09)
> Примечание: ручей с холма всегда течет обратно градиенту в любой своей точке.

Какому градиенту?

← →
olookin © ( 2004-09-10 10:12 ) [3]

grad(Ф) = d(Ф)/dx + d(Ф)/dy + d(Ф)/dz

для одномерного случая только d(Ф)/dx

Сообщите, если я неправ.

← →
Romkin © ( 2004-09-10 10:14 ) [4]

Думкин © (10.09.04 10:11) [2] Градиенту потенциала гравитационного поля :)))

olookin © (10.09.04 10:12) [3] Я сказал вектор! А у тебя скалярная величина :))

← →
olookin © ( 2004-09-10 10:18 ) [6]

[4] Romkin © (10.09.04 10:14)

Значит, я был неправ.

← →
Romkin © ( 2004-09-10 10:19 ) [7]

← →
Romkin © ( 2004-09-10 10:20 ) [8]

olookin © (10.09.04 10:18) [6] Почти прав
grad(Ф) = (d(Ф)/dx, d(Ф)/dy, d(Ф)/dz)

← →
Думкин © ( 2004-09-10 10:23 ) [9]

Только наверное не форму, а такая функция H(x,y)

← →
Romkin © ( 2004-09-10 10:36 ) [11]

Думкин © (10.09.04 10:24) [10] Ага. Hill(x,y) :)))

← →
olookin © ( 2004-09-10 10:38 ) [12]

[8] Romkin © (10.09.04 10:20)

А вот тут ты не прав. Раз вектор представляется координатами, то надо и базисы отобразить.

> olookin © (10.09.04 10:38) [12]
> [8] Romkin © (10.09.04 10:20)
>
> А вот тут ты не прав. Раз вектор представляется координатами,
> то надо и базисы отобразить.

Добавь в [3] i, j, k и будет щасье:

> [13] DiamondShark © (10.09.04 11:26)

В строгом направлении? Или я неверно толкую слово противоположно?

← →
dr Tr0jan ( 2004-09-10 11:38 ) [16]

А можно привести пример с конкретными числами7

← →
Alx2 © ( 2004-09-10 11:44 ) [17]

На ручей, кроме гравитации, ещё какие-то силы действуют?

← →
Думкин © ( 2004-09-10 11:56 ) [19]

> Думкин © (10.09.04 11:56) [19]

Так составляющая против градиента есть? Есть. В чём проблем?

← →
Думкин © ( 2004-09-10 12:05 ) [21]

← →
Думкин © ( 2004-09-10 12:08 ) [22]

> [20] DiamondShark © (10.09.04 12:04)

Есть, но все-таки не в противоположную. А с составляющей не равной 0. Только это.
Я тебе кстати предложил:
> Или я неверно толкую слово противоположно?
не зацепился. Ну и ладно.

> Думкин © (10.09.04 12:08) [22]

Об чём шумим? Не пойму.

← →
Думкин © ( 2004-09-10 12:14 ) [24]

> [23] DiamondShark © (10.09.04 12:13)

Сам не знаю. 🙂
Кстати у автора в сабже Grad, а потом речь о grad. А это немного разные вещи. Если второе для скалярных функций, то первое для произвольных тензоров.

← →
pasha_golub © ( 2004-09-10 12:29 ) [25]

А можно я немножко поламерю?

1. Разве grad єто функция? Это ж вроде оператор.
2. На ручей действует сила реакции опоры, ну в смысле холм опирается. Потому и в Каспийское море, а не в центр Земли.

← →
Думкин © ( 2004-09-10 12:35 ) [26]

← →
dr Tr0jan ( 2004-09-10 12:39 ) [27]

Ну ладно, допустим у меня есть конкретное численное значение напряжённости в данной точке, причём никаких функций не задано. А как мне найти значение потенциала в этой же точке (см. начало)?

← →
pasha_golub © ( 2004-09-10 12:40 ) [28]

Думкин © (10.09.04 12:35) [26]
1. Ну оператор. Функция из одного множества в другое. Просто множества такие.

> причём никаких функций не задано.

Тогда курить бамбук. Оператор применим к скалярному полю, то бишь к функции, задающей пространственное распределение величины.

Только по значению напряжённости потенциал не определить.

Пример: поле в плоском конденсаторе. Напряжённость везде одинаковая, а потенциал разный.

← →
Думкин © ( 2004-09-10 12:54 ) [31]

Источник